O întrebare importantă este: cum sunt distribuite numerele prime printre numere întregi? Răspunsul este, în foarte puține cuvinte, destul de aleatoriu, având în vedere anumite statistici de bază…
 Bill Casselman
Bill Casselman
Universitatea din British Columbia, Vancouver, Canada
Email Bill Casselman
| |
|
Introducere
Cu mulți ani în urmă s-a conchis că există un număr infinit de perechi de numere prime $p$, $q$ cu $q = p+2$. S-au înregistrat unele progrese recente (și celebre) în această problemă. Voi vorbi puțin despre progresele recente, dar voi discuta în schimb despre ceea ce ne așteptăm – mai degrabă decât despre ceea ce știm – despre astfel de perechi. Nimic din ceea ce voi spune nu este nou și, într-o oarecare măsură, nu am făcut decât să elaborez ceea ce Andrew Granville spune în nota sa recentă de expunere a progreselor recente.
Câte numere prime ne așteptăm?
Un număr prim este un număr întreg pozitiv care nu are divizori în afară de el însuși și $1$. Definiția este simplă, dar de îndată ce începem să explorăm semnificația numerelor prime ne dăm seama că acestea prezintă un comportament mult mai subtil. O întrebare importantă este: cum sunt distribuite numerele prime printre numerele întregi? Răspunsul este, în foarte puține cuvinte, destul de aleatoriu, având în vedere anumite statistici de bază. Ce vreau să spun prin aceasta?
Ei bine, iată un tablou pătrat care reprezintă toate numerele prime până la 400$:

Există câteva modele în acest tablou, unele dintre ele pe care le voi comenta mai târziu. Cele mai multe dintre cele pe care le percepeți sunt cauzate de un artefact al afișajului. De exemplu, fiecare altă coloană este practic goală, iar acest lucru se datorează faptului că singurul prim par este $2$. De asemenea, fiecare a cincea coloană este practic goală. Mai interesante sunt perechile de prime gemene (dintre care unele nu sunt atât de vizibile deoarece se împart în două rânduri, cum ar fi $59$, $61$) și, de asemenea, unele modele legate de ultimele cifre afișate. Acestea sunt ceea ce s-ar putea numi modele locale. Nu există niciunul global aparent.
Au fost depuse multe eforturi pentru a găsi modalități extrem de eficiente de a produce numere prime, dar în zilele noastre chiar și un program foarte simplu are nevoie de puțin timp pentru a realiza liste mari de numere prime. Unul dintre cele mai fructuoase programe va face o listă mare de numere prime și apoi o va folosi pentru a calcula funcția $\pi(n)$, numărul de numere prime $\le n$.
Un lucru pentru care poate fi folosit acest lucru este de a obține o idee aproximativă a frecvenței numerelor prime. Există $135$ numere prime în intervalul $$:
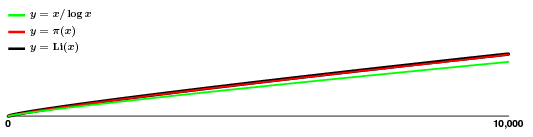
Aproximația arată foarte bine! Deci, chiar dacă $\pi(x)$ sare puțin, aparent fără prea mult tipar, avem o estimare destul de bună pentru aceasta, ceea ce înseamnă că avem o idee bună despre cum cresc numerele prime, cel puțin în medie.
Trebuie avut în vedere, totuși, că aparenta netezime este înșelătoare. De aproape, iată cum arată cele două curbe de sus:

Comentarii?
Raționamenteuristic despre prime gemene
Primele gemene sunt o pereche $p$, $p+2$ care sunt ambele prime. De exemplu, dintr-unul din graficele de mai sus vedem prime gemene $$ , , , , , , , , $$
și altele. S-a conchis că există un număr infinit de astfel de numere, dar, deși există multe dovezi empirice în acest sens, ele nu au fost încă dovedite.
Poate cea mai puternică dovadă este o formulă care aproximează remarcabil de bine numărul $\pi_{2}(x)$ de prime gemene $\le x$. Nu sunt foarte sigur de originea acestei formule, dar ea a apărut pentru prima dată într-o lucrare a lui G. H. Hardy și J. E. Littlewood (ei înșiși o pereche de numere prime gemene) datată 1923. Lucrarea conține mai multe formule similare, toate bazate pe aceeași metodă, pe care ei o folosiseră pentru a ataca mai multe probleme anterior. Aceasta era metoda cercului lor. Derivarea formulei lor pentru $\pi_{2}(x)$ nu este deloc riguroasă, dar este foarte convingătoare. Există o relatare succintă a acesteia într-un apendice la articolul lui Andrew Granville.
Dar imediat după cel de-al Doilea Război Mondial, Lordul Cherwell (Frederick Lindemann) a sugerat o derivare probabilistică mai elementară (și încă nu riguroasă). Aceasta a dus la o colaborare cu E. M. Wright și, în cele din urmă, la o publicație comună postumă. Acest lucru este explicat în secțiunea 22.20 din binecunoscutul text al lui Hardy și Wright. O versiune puțin mai elementară a acesteia poate fi găsită, de asemenea, într-un apendice al articolului lui Granville (secțiunea 2.5). Îl urmez.
Punctul de plecare al raționamentului plauzibil este estimarea noastră pentru $\pi(x)$, numărul de numere prime mai mici sau egale cu $x$. Ideea de bază a derivării este că numerele prime sunt, într-o bună măsură, distribuite aleatoriu. Știm că în vecinătatea lui $x$ densitatea numerelor prime este de aproximativ $1/\log x$. Dacă numerele prime ar fi distribuite aleatoriu, atunci probabilitatea ca oricare două numere date în apropierea lui $x$ să fie prime ar fi doar produsul probabilităților locale, care este $1/\log^{2} x$. Acesta este, cu siguranță, un raționament specios, deoarece, dacă $n > 2$, probabilitatea ca atât $n$, cât și $n+1$ să fie numere prime este $0$, în timp ce faptul că $p$ este un număr prim ar părea să crească șansele ca $p+2$ să fie un număr prim. Există considerații similare de care trebuie să se țină seama din cauza posibilei divizibilități cu alte numere prime mici, de asemenea, în vecinătatea lui $x$.
Există un fapt simplu în această poveste. Dacă $q$ este un număr prim oarecare, atunci probabilitatea de a alege la întâmplare un număr întreg care nu este divizibil cu $q$ este $1-1/q$. Probabilitatea de a alege două care nu sunt divizibile cu $q$ este deci produsul $(1 – 1/q)^{2}$. Să presupunem că $p$ și $p+2$ sunt amândoi numere prime, atunci nici $p$, nici $p+2$ nu este divizibil cu $q$. Dacă $q = 2$, acest lucru se întâmplă de 1/2$ ori. Dacă $q \ne 2$, probabilitatea ca $p \nu este egal cu 0$ și $p \nu este egal cu -2$ modulo $q$ este $(1 – 2/q)$. Datorită Teoremei restului chinezesc, divizibilitatea cu două numere prime este un eveniment independent. Așadar, dacă $x$ este mare și $Q$ este relativ mic, probabilitatea ca orice pereche de numere $m$ și $n$ din apropierea lui $x$ să nu fie multiplu al vreunui număr prim până la $Q$ este $$ { 1\supra 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} } \, . $$
Să fie $\Gamma_{Q}$ raportul dintre acesta și $\prod_{q \le Q}(1 – 2/q)$: $$ \Gamma_{Q} = { 1\supra 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \ peste (1 – 2/q) } $$ Avem $$ { 1 – 2/q \ peste (1-1/q)^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \ peste (1 – 1/q)^{2} } = 1 – { 1 \over (q -1)^{2} } \, . $$ Un criteriu standard afirmă că acest produs converge dacă suma $\sum 1/(q-1)^{2}$ converge. Dar acesta converge, deoarece testul integral ne spune că $\suma 1/n^{2}$ converge. Prin urmare, acest produs converge de fapt la un număr $\Pi_{\infty}$ pe măsură ce $Q \rightarrow \infty$. Fie $C_{2}$ inversul său. Secțiunea 2.5 din articolul lui Granville spune că ar trebui să fie intuitiv rezonabil în acest punct că numărul $\pi_{2}(x)$ de prime gemene $\le x$ este aproximat prin $$ \Pi_{2}(x) = C_{2} \int_{2}^{\infty} { dx \ peste \log^{2} x } \, . $$
Textul lui Hardy și Wright prezintă o analiză mai atentă care face saltul intuitiv un pic mai clar.
Valoarea constantei de aici a fost calculată cu mult timp în urmă de J. W. Wrench ca fiind de aproximativ $1.32032363163169373914785562422002911155686525 \ldots $. Iată o comparație a unor valori ale lui $\pi_{2}(x)$ și ale formulei în intervalul $$$: $$ \matrix{ n & 10.000 & 20.000 & 30.000 & 40.000 & 50.000 \cr \pi_{2}(n) & 205\phantom{.0} & 342 \phantom{.0} & 467 \phantom{.0} & 591 \phantom{.0} & 705 \phantom{.0} & \cr \Pi_{2}(x) & 214.2 & 357.7 & 486.7 & 607.4 & 722.5 \cr } $$ $$ $$ \matrix{ n & 60.000 & 70.000 & 80.000 & 90.000 & 100.000 \cr \pi_{2}(n) & 811 \phantom{.0} & 905 \phantom{.0} & 1007 \phantom{.0} & 1116 \phantom{.0} & 1224\phantom{.0} \cr \Pi_{2}(x) & 833.3 & 940.9 & 1045.7 & 1148.2 & 1248.7 \cr } $$
Comentari?
Conjectura lui Dickson
Primii gemeni sunt un caz special a ceva mult mai general. Ne putem întreba dacă există un număr infinit de perechi $p$, $p+4$ sau $p$, $p+6$ care sunt prime? Sau $p$, $p+10$? Cazul lui $p$ și $p+10$ este cu siguranță sugerat de una dintre imaginile de mai sus, în care astfel de perechi sunt ușor vizibile. Ce ziceți de un fel de triple? Să presupunem că $a_{1}$, $a_{2}$, $\ldots$ , $a_{k}$ alcătuiesc o matrice de numere întregi. Ne putem aștepta să existe un număr infinit de seturi $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$ care să fie toate prime?
Trebuie să fim un pic mai atenți. Nu există perechi prime de forma $p$, $p+1$ (trecut $p = 2$), deoarece unul dintre aceste două numere trebuie să fie divizibil cu $2$. În mod similar, după $p = 3$ nu există triplete prime $p$, $p+2$, $p+4$, deoarece unul dintre acestea trebuie să fie divizibil cu $3$.
Acest ultim exemplu ar trebui să fie lămuritor. Numărul $p+4$ este divizibil cu $3$ dacă și numai dacă $p+1$ este divizibil cu $3$. Prin urmare, $3$ împarte unul dintre numerele $p$, $p+2$, $p+4$ dacă și numai dacă împarte $p$, $p+1$, $p+2$. Dar acest lucru se va întâmpla cu siguranță, deoarece ultima triplă acoperă în mod clar toate numerele modulo $3$.
În general, se spune că $p$ este un obstacol pentru matricea $(a_{i})$ dacă $p$ împarte întotdeauna cel puțin unul din fiecare secvență $n+a_{i}$ ($i = 1$, $\ldots$, $k$). Acest lucru se întâmplă dacă și numai dacă numerele $a_{i} \; {\rm mod} \, p$ umplu tot $Z/p$.
Acest lucru nu se poate întâmpla niciodată dacă $p > k$, astfel încât, pentru a verifica dacă un anumit $p$ obstrucționează $(a_{i})$ trebuie doar să verificăm dacă $a_{i}$ acoperă $Z/p$ pentru toți $p \le k$. Numim matricea $(a_{i})$ admisibilă dacă nu are obstrucții prime.
De exemplu, $(1,3,7,9)$ este o matrice admisibilă, deoarece, după cum se poate verifica ușor, nici $2$, nici $3$ nu reprezintă o obstrucție. Mai multe secvențe prime care se încadrează în acest tipar pot fi văzute într-una din diagramele de mai sus. Alte exemple sunt: (a) orice $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
Există seturi admisibile arbitrar de mari. De fapt:
Teoremă. Dacă $a_{1}$ până la $a_{k}$ este un ansamblu oarecare de numere prime distincte $> k$, acestea alcătuiesc un ansamblu admisibil.
De ce se întâmplă acest lucru? Dacă $p$ este orice număr prim în care $p> k$, atunci am văzut deja că nu poate fi un obstacol. Dar dacă $p \le k$, atunci nu poate împărți nici unul dintre $a_{i}$, dintre care nici unul nu poate fi congruent cu $0$ modulo $p$. Deci $a_{i}$ nu umple $Z/p$.
Un caz special al unei conjecturi făcute inițial de L. E. Dickson este că dacă nu există obstrucții prime pentru $(a_{i})$ atunci există un număr infinit de secvențe prime de forma $(n +a_{i})$.
Ce s-a întâmplat recent
Nu este locul potrivit pentru a spune întreaga poveste, care a fost acoperită amănunțit în alte locuri. Recomand în special articolul Quanta de Erica Klarreich pentru o relatare populară și eseul lui Granville pentru una mai tehnică. Vreau doar să precizez un pic mai precis decât în relatarea lui Klarreich care este cel mai faimos dintre noile rezultate.
Se datorează lui Yitang Zhang. Cea mai simplă afirmație a ceea ce a demonstrat el este că există un număr infinit de intervale $[n, n+70.000.000.000)$ care conțin cel puțin două numere prime. Această afirmație este mai slabă decât conjectura primelor gemene, dar, din punct de vedere conceptual, este foarte apropiată de ea. În lucrările ulterioare (realizate de mulți matematicieni), dimensiunea intervalului a fost redusă drastic, dar se presupune că nu există nicio modalitate de a-l reduce la $2$ cu metodele actuale.
După cum a explicat Granville, primul și probabil principalul rezultat al lui Zhang este că există $k$ cu proprietatea că dacă $a_{1}$, $\ldots$ , $a_{k}$ este un set admisibil de $k$ elemente, atunci există un număr infinit de $n$ astfel încât $\{ n +a_{i} \}$ conține cel puțin două numere prime. (În articolul Quanta al lui Klarreich, matricea este numită „pieptene”. Rețineți că, în conformitate cu conjectura lui Dickson, ne-am aștepta să putem spune că toți $k$ sunt numere prime). De fapt, Zhang a demonstrat că această afirmație este adevărată pentru un anumit $k =3.500.000$ care se întinde pe un interval de 70.000.000$. Consecința, devenită celebră până acum, este că pentru un anumit $m \lt 70.000.000$ există un număr infinit de perechi prime $p$, $p+m$.
Citește mai departe
- Lord Cherwell și E. M. Wright, „The frequency of prime patterns”, The Quarterly Journal of Mathematics 11 (1960).
Cei care cunosc câte ceva din viața lui Lord Cherwell, cunoscut și sub numele de Frederick Lindemann, vor fi foarte surprinși să afle despre contribuția sa la teoria numerelor. Biografia de pe Wikipedia nu sugerează în mod adecvat toate motivele pentru reputația sa proastă ca principal consilier științific al lui Churchill în timpul celui de-al Doilea Război Mondial.
- L. E. Dickson, „A new extension of Dirichlet’s theorem on prime numbers”, Messenger of Mathematics 33.
Vezi și intrarea din Wikipedia despre conjectura lui Dickson.
- Andrew Granville, „Primes in intervals of bounded length”. Disponibil de pe pagina sa de internet.
- G. H. Hardy, Ramanujan, Cambridge University Press.
Secțiunea 2.5 conține o derivare ideală a unei formule posibile pentru $\pi(x)$.
- G. H. Hardy și J. E. E. Littlewood, „Some problems of ‘Partitio numerorum’ III: on the expression of a number as a sum of prime”, Acta Mathematica 44 (1923).
- G. H. Hardy și E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, „Together and alone, closing the prime gap”, Quanta November 19, 2013.
- B. Riemann, „On the number of prime numbers less than a given quantity”. O traducere în engleză a acestui clasic de către David Wilkins este disponibilă printr-un link din Wikipedia.
Printre altele, aceasta schițează o derivare a formulei aproximative pentru $\pi(x)$.
- J. W. Wrench, „Evaluation of Artin’s constant and the twin-prime constant”, Mathematics of Computation 76 (1961).
Un calcul timpuriu al lui $C_{2}$.
- Liste de prime până la 1.000.000.000.000.000$
- O listă a primelor 20.000 de prime gemene.
 Bill Casselman
Bill Casselman
Universitatea British Columbia, Vancouver, Canada
Email Bill Casselman
.