Nu se întâmplă prea des ca o ecuație matematică să ajungă în presa națională, cu atât mai puțin la radioul popular sau, cel mai uimitor dintre toate, să fie subiectul unei dezbateri în parlamentul britanic. Cu toate acestea, în 2003, vechea și buna ecuație pătratică, despre care am învățat cu toții la școală, a fost toate aceste lucruri.
De unde începem

Totul a început la o întâlnire a Uniunii Naționale a Profesorilor. Ecuația pătratică a fost prezentată națiunii ca un exemplu de tortură crudă aplicată de matematicieni asupra bieților școlari neștiutori. Intrigată de această acuzație, ecuația pătratică a acceptat un rol principal la o emisiune radiofonică la oră de maximă audiență, unde a fost chestionată de un intervievator formidabil, mai obișnuit să se confrunte cu primul ministru. The Times (Londra) a ocupat spațiu în rubrica sa de lider, rezervată de obicei discuțiilor importante despre sănătatea morală (sau nu) a lumii moderne, pentru a proclama că ecuația pătratică este inutilă, că matematica este inutilă și că, oricum, nimeni nu vrea să studieze matematica, așa că de ce să se deranjeze. Preocupați ca nu cumva admiterile periculoase ale ecuației pătratice să rămână necontestate, importanța vitală a ecuației pentru supraviețuirea Regatului Unit a fost dezbătută (s-a adoptat un punct de vedere pozitiv, poate vă veți bucura să aflați) în Camera Comunelor britanică.
Unde s-ar termina totul? Era cu adevărat moartă ecuația pătratică? Îi păsa cuiva? Sunt matematicienii cu adevărat niște monștri malefici, care nu vor decât să aplice ecuații pătratice unei generații mai tinere ca mijloc de a le corupe sufletele nemuritoare?
Poate că da, dar nu este chiar vina ecuației pătratice. De fapt, ecuația pătratică a jucat un rol esențial nu numai în întreaga civilizație umană așa cum o cunoaștem, ci și în posibila detectare a altor civilizații extraterestre și chiar în activități moderne vitale precum vizionarea televiziunii prin satelit. Ce altceva, în afară de natura revelației divine, ar putea fi considerat că a avut un asemenea impact asupra vieții așa cum o cunoaștem noi? Într-adevăr, într-un sens foarte real, ecuațiile pătratice vă pot salva viața.
Babilonienii
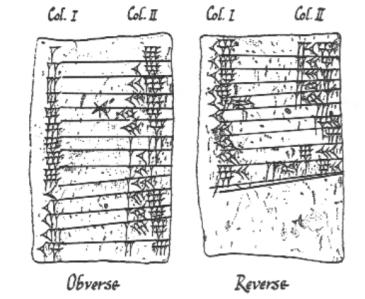
Tabuletele cuneiforme babiloniene care înregistrează cele 9 tabele de timp
Totul a început în jurul anului 3000 î.Hr. cu babilonienii. Aceștia au fost una dintre primele civilizații din lume și au venit cu câteva idei mărețe, cum ar fi agricultura, irigațiile și scrierea. Ei au trasat traiectoria Soarelui, a Lunii și a planetelor și le-au înregistrat pe tăblițe de lut (pe care le puteți vedea și acum la British Museum). Babilonienilor le datorăm ideile moderne despre unghiuri, inclusiv modul în care cercul este împărțit în 360 de grade (din cauza unei mici erori de calcul, una pe zi). Babilonienilor le datorăm, de asemenea, invenția mai puțin plăcută a (temutului) fisc. Și acesta a fost unul dintre motivele pentru care babilonienii au avut nevoie să rezolve ecuații pătratice.
Să presupunem că sunteți un fermier babilonian. Undeva, în ferma dumneavoastră, aveți un câmp pătrat pe care creșteți o anumită cultură. Ce cantitate din cultura ta poți cultiva pe acest câmp? Dublați lungimea fiecărei laturi a câmpului și veți constata că puteți cultiva o cantitate de patru ori mai mare decât înainte. Motivul pentru care se întâmplă acest lucru este faptul că cantitatea de cultură pe care o puteți cultiva este proporțională cu suprafața câmpului, care la rândul ei este proporțională cu pătratul lungimii laturii. În termeni matematici, dacă  este lungimea laturii câmpului,
este lungimea laturii câmpului, 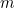 este cantitatea de cultură pe care o puteți cultiva pe un câmp pătrat de lungime laterală 1, iar
este cantitatea de cultură pe care o puteți cultiva pe un câmp pătrat de lungime laterală 1, iar  este cantitatea de cultură pe care o puteți cultiva, atunci
este cantitatea de cultură pe care o puteți cultiva, atunci
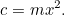 |
Aceasta este prima noastră ecuație pătratică, goală și pâlpâind în lumina soarelui. Ecuațiile pătratice și ariile sunt legate între ele ca frații și surorile din aceeași familie. Cu toate acestea, deocamdată nu trebuie să rezolvăm nimic – până când sosește fiscul, bineînțeles! Vesel, el îi spune fermierului: „Vreau să-mi dai recolte pentru a plăti impozitele de pe ferma ta”. Fermierul are acum o dilemă: cât de mare este câmpul de care are nevoie pentru a cultiva această cantitate de recoltă? Noi putem răspunde ușor la această întrebare, de fapt
recolte pentru a plăti impozitele de pe ferma ta”. Fermierul are acum o dilemă: cât de mare este câmpul de care are nevoie pentru a cultiva această cantitate de recoltă? Noi putem răspunde ușor la această întrebare, de fapt
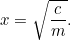 |
Căutarea rădăcinilor pătrate cu ajutorul unui calculator este ușoară pentru noi, dar era mai degrabă o problemă pentru babilonieni. De fapt, ei au dezvoltat o metodă de aproximare succesivă a răspunsului care este identică cu algoritmul (numit metoda Newton-Raphson) folosit de calculatoarele moderne pentru a rezolva probleme mult mai dificile decât ecuațiile pătratice.
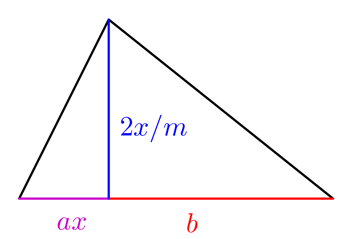
Acum, nu toate câmpurile sunt pătrate. Să presupunem acum că fermierul are un câmp cu o formă mai ciudată, cu două secțiuni triunghiulare, așa cum se arată în dreapta.
Pentru valori adecvate ale  și
și 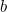 cantitatea de recoltă pe care fermierul o poate cultiva pe acest câmp este dată de
cantitatea de recoltă pe care fermierul o poate cultiva pe acest câmp este dată de
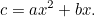 |
Aceasta seamănă mult mai mult cu ecuația pătratică cu care suntem obișnuiți, și chiar și sub ochiul rău al fiscului, este mult mai greu de rezolvat. Cu toate acestea, babilonienii au găsit din nou răspunsul. Mai întâi împărțim la  pentru a obține
pentru a obține
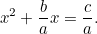 |
Acum completăm pătratul folosind faptul că
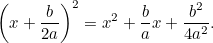 |
Combinând acest lucru cu ecuația inițială avem
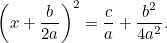 |
Aceasta este acum o ecuație pe care o putem rezolva prin extragerea rădăcinilor pătrate. Rezultatul este celebra „formulă 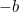 „:
„:
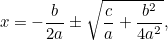 |
care poate fi rescrisă sub forma
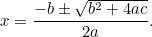 |
(Formula are de obicei „-„.4ac”, deoarece ecuația pătratică se scrie de cele mai multe ori sub forma „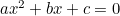 „.)
„.)
Faptul că luarea unei rădăcini pătrate poate da un răspuns pozitiv sau negativ conduce la rezultatul remarcabil că o ecuație pătratică are două soluții. Cam atât despre enigmele matematice care au doar o singură soluție!
Acum, aici se oprește adesea predarea ecuațiilor pătratice. Am ajuns la acel obiect îndrăgit de toți jurnaliștii atunci când intervievează matematicieni – o formulă. Se pot inventa întrebări nesfârșite care presupun introducerea valorilor 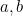 și
și  în formulă pentru a obține (două) răspunsuri. Dar nu despre asta este vorba deloc în matematică. Găsirea unei formule este doar primul pas pe un drum lung. Trebuie să ne întrebăm: ce înseamnă formula; ce ne spune ea despre univers; contează cu adevărat să avem o formulă? Să vedem acum unde ne va duce această formulă.
în formulă pentru a obține (două) răspunsuri. Dar nu despre asta este vorba deloc în matematică. Găsirea unei formule este doar primul pas pe un drum lung. Trebuie să ne întrebăm: ce înseamnă formula; ce ne spune ea despre univers; contează cu adevărat să avem o formulă? Să vedem acum unde ne va duce această formulă.
O surpriză pentru greci, un pic de origami matematic și un simț al proporțiilor
Mergem acum repede înainte cu 1000 de ani până la grecii antici și vedem ce au făcut ei din ecuațiile pătratice. Grecii au fost matematicieni superbi și au descoperit o mare parte din matematica pe care o folosim și astăzi. Una dintre ecuațiile pe care erau interesați să le rezolve era ecuația pătratică (simplă)
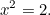 |

Ei știau că această ecuație are o soluție. De fapt, ea este lungimea ipotenuzei unui triunghi dreptunghic care avea laturile de lungime unu.
Din teorema lui Pitagora rezultă că dacă un triunghi dreptunghictriunghi dreptunghic are laturile  și
și  mai scurte și ipotenuza
mai scurte și ipotenuza  atunci
atunci
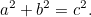 |
Dacă punem 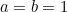 și
și  atunci
atunci 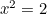 . Astfel
. Astfel 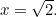
Deci, ce este  în acest caz? Sau, ca să punem întrebarea pe care o puneau grecii, ce fel de număr este acesta? Motivul pentru care acest lucru era important consta în simțul grecului pentru proporții. Ei credeau că toate numerele sunt proporționale între ele. Mai exact, acest lucru însemna că toate numerele erau fracții de forma
în acest caz? Sau, ca să punem întrebarea pe care o puneau grecii, ce fel de număr este acesta? Motivul pentru care acest lucru era important consta în simțul grecului pentru proporții. Ei credeau că toate numerele sunt proporționale între ele. Mai exact, acest lucru însemna că toate numerele erau fracții de forma 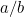 unde
unde  și
și  sunt numere întregi. Numere precum 1/2, 3/4 și 355/113 sunt toate exemple de fracții. Era firesc să ne așteptăm ca
sunt numere întregi. Numere precum 1/2, 3/4 și 355/113 sunt toate exemple de fracții. Era firesc să ne așteptăm ca  să fie, de asemenea, o fracție. Surpriza uriașă a fost că nu este. De fapt,
să fie, de asemenea, o fracție. Surpriza uriașă a fost că nu este. De fapt,
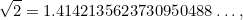 |
unde punctele  înseamnă că expansiunea zecimală a lui
înseamnă că expansiunea zecimală a lui  continuă până la infinit fără niciun model perceptibil. (Vom reîntâlni această situație mai târziu, când vom învăța despre haos.)
continuă până la infinit fără niciun model perceptibil. (Vom reîntâlni această situație mai târziu, când vom învăța despre haos.)
 a fost primul număr irațional (adică un număr care nu este o fracție, sau rațional), care a fost recunoscut ca atare. Alte exemple includ
a fost primul număr irațional (adică un număr care nu este o fracție, sau rațional), care a fost recunoscut ca atare. Alte exemple includ 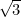 ,
,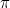 ,
,  și, de fapt, „majoritatea” numerelor. A fost nevoie până în secolul al XIX-lea pentru a avea o modalitate bună de a ne gândi la aceste numere. Descoperirea faptului că
și, de fapt, „majoritatea” numerelor. A fost nevoie până în secolul al XIX-lea pentru a avea o modalitate bună de a ne gândi la aceste numere. Descoperirea faptului că  nu era un număr rațional a provocat atât un mare entuziasm (100 de boi au fost sacrificați ca urmare), cât și un mare șoc, descoperitorul fiind nevoit să se sinucidă. (Fie ca acesta să fie un avertisment teribil pentru cei pasionați de matematică!) În acest moment, grecii au renunțat la algebră și s-au orientat spre geometrie.
nu era un număr rațional a provocat atât un mare entuziasm (100 de boi au fost sacrificați ca urmare), cât și un mare șoc, descoperitorul fiind nevoit să se sinucidă. (Fie ca acesta să fie un avertisment teribil pentru cei pasionați de matematică!) În acest moment, grecii au renunțat la algebră și s-au orientat spre geometrie.
Departe de a fi un număr obscur, întâlnim  în mod regulat: ori de câte ori folosim o bucată de hârtie A4. În Europa, dimensiunile hârtiei sunt măsurate în dimensiuni A, A0 fiind cea mai mare, cu o suprafață de
în mod regulat: ori de câte ori folosim o bucată de hârtie A4. În Europa, dimensiunile hârtiei sunt măsurate în dimensiuni A, A0 fiind cea mai mare, cu o suprafață de 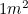 . Dimensiunile A au o relație specială între ele. Dacă facem acum un pic de origami, luând o foaie de hârtie A1 și împăturind-o apoi în două (de-a lungul laturii sale cele mai lungi), obținem hârtie A2. Dacă o împăturim din nou în două, obținem A3, și din nou A4 etc. Cu toate acestea, hârtia este concepută astfel încât proporțiile fiecăreia dintre dimensiunile A să fie aceleași – adică fiecare bucată de hârtie are aceeași formă.
. Dimensiunile A au o relație specială între ele. Dacă facem acum un pic de origami, luând o foaie de hârtie A1 și împăturind-o apoi în două (de-a lungul laturii sale cele mai lungi), obținem hârtie A2. Dacă o împăturim din nou în două, obținem A3, și din nou A4 etc. Cu toate acestea, hârtia este concepută astfel încât proporțiile fiecăreia dintre dimensiunile A să fie aceleași – adică fiecare bucată de hârtie are aceeași formă.
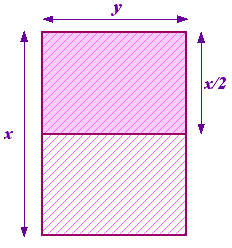
Ne putem pune întrebarea ce proporție este aceasta. Începeți cu o bucată de hârtie cu laturile x și y, cu x cea mai lungă latură. Acum împărțiți-o în două pentru a obține o altă bucată de hârtie cu laturile y și x/2, y fiind acum cea mai lungă latură. Acest lucru este ilustrat în dreapta. Proporțiile primei bucăți de hârtie sunt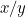 , iar cele ale celei de-a doua sunt
, iar cele ale celei de-a doua sunt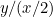 sau
sau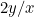 . Dorim ca aceste două proporții să fie egale. Aceasta înseamnă că
. Dorim ca aceste două proporții să fie egale. Aceasta înseamnă că
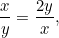 |
sau
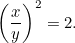 |
O altă ecuație pătratică! Din fericire este una pe care am întâlnit-o deja. Rezolvând-o găsim că
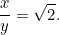 |
Acest rezultat este ușor de verificat. Este suficient să luați o foaie de hârtie A4 (sau A3 sau A5) și să măsurați laturile. Putem, de asemenea, să calculăm dimensiunea fiecărei foi. Aria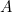 a unei bucăți de hârtie A0 este dată de
a unei bucăți de hârtie A0 este dată de
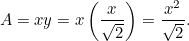 |
Dar știm că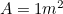 deci avem o altă ecuație pătratică pentru cea mai lungă latură
deci avem o altă ecuație pătratică pentru cea mai lungă latură a lui A0, dată de
a lui A0, dată de
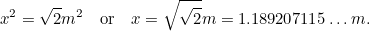 |
Aceasta înseamnă că cea mai lungă latură a lui A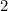 este dată de
este dată de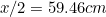 (de ce?), iar cea a lui A
(de ce?), iar cea a lui A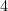 de
de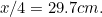 . Verificați aceste rezultate pe propriile foi de hârtie.
. Verificați aceste rezultate pe propriile foi de hârtie.
Hârtia folosită în Statele Unite, numită foolscap, are o proporție diferită. Pentru a vedea de ce, ne întoarcem la greci și la o altă ecuație pătratică. După ce a provocat atâtea necazuri, ecuația pătratică se răscumpără în căutarea proporțiilor perfecte: o căutare care continuă și astăzi în proiectarea decorurilor de film și care poate fi observată în multe aspecte ale naturii.
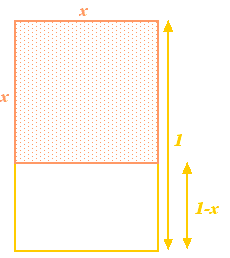
Să începem cu un dreptunghi, apoi să eliminăm din el un pătrat cu lungimea laturii egală cu cea mai scurtă latură a dreptunghiului. Dacă cea mai lungă latură a dreptunghiului are lungimea 1, iar cea mai scurtă latură are lungimea  , atunci pătratul are laturile de lungime
, atunci pătratul are laturile de lungime  . Eliminându-l din dreptunghi se obține un dreptunghi mai mic cu latura cea mai lungă
. Eliminându-l din dreptunghi se obține un dreptunghi mai mic cu latura cea mai lungă  și latura cea mai mică
și latura cea mai mică 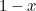 . Până aici, atât de abstract. Cu toate acestea, grecii credeau că dreptunghiul care are cele mai estetice proporții (așa-numitul dreptunghi de aur) este acela pentru care dreptunghiul mare și cel mic construite mai sus au aceleași proporții. Pentru ca acest lucru să fie posibil trebuie să avem
. Până aici, atât de abstract. Cu toate acestea, grecii credeau că dreptunghiul care are cele mai estetice proporții (așa-numitul dreptunghi de aur) este acela pentru care dreptunghiul mare și cel mic construite mai sus au aceleași proporții. Pentru ca acest lucru să fie posibil trebuie să avem
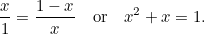 |
Aceasta este încă o ecuație pătratică: una foarte importantă care apare în tot felul de aplicații. Are soluția (pozitivă)
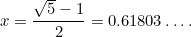 |
Numărul  se numește raportul de aur și este adesea notat cu litera greacă
se numește raportul de aur și este adesea notat cu litera greacă 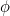 .
.

Dreptunghiul de aur poate fi văzut în forma ferestrelor, în special pe casele georgiene. Mai recent, Raportul de Aur poate fi întâlnit și ca „formă perfectă” pentru fotografii și imagini de film. Ecuația pătratică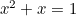 apare, de asemenea, în studiile privind populațiile de iepuri și în modelul în care sunt dispuse semințele de floarea-soarelui și frunzele de pe tulpinile plantelor. Toate acestea sunt legate de raportul de aur prin intermediul secvenței Fibonacci, care este dată de
apare, de asemenea, în studiile privind populațiile de iepuri și în modelul în care sunt dispuse semințele de floarea-soarelui și frunzele de pe tulpinile plantelor. Toate acestea sunt legate de raportul de aur prin intermediul secvenței Fibonacci, care este dată de
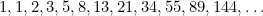 |

Semințe de floarea-soarelui, aranjate cu ajutorul numerelor Fibonacci |
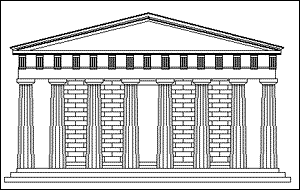
Parthenonul, care întruchipează Raportul de Aur |
În această secvență, fiecare termen este suma celor doi termeni anteriori. Fibonacci a descoperit-o în secolul al XV-lea, în încercarea de a prezice viitoarea populație de iepuri. Dacă se ia raportul dintre fiecare termen și cel de după el, se obține secvența de numere
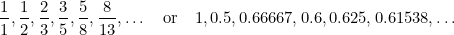 |
, iar aceste numere se apropie din ce în ce mai mult de (ați ghicit) Raportul de Aur 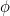 .
.
Prin găsirea ambelor rădăcini ale ecuației pătratice de mai sus putem găsi de fapt o formulă pentru cel de-al n-lea termen din secvența Fibonacci. Dacă  este al
este al 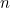 lea astfel de număr cu
lea astfel de număr cu 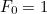 și
și 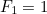 , atunci
, atunci  este dat de formula
este dat de formula
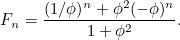 |
Conicele leagă ecuațiile pătratice de stele

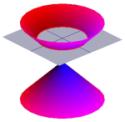
Grecii erau, de asemenea, foarte interesați de forma conurilor. imaginea din stânga prezintă un con tipic.
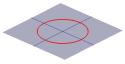
Jumătate din con poate fi vizualizată ca răspândirea luminii care vine de la o lanternă. Acum, dacă luminați o torță pe o suprafață plană, cum ar fi un perete, atunci veți vedea diverse forme pe măsură ce mișcați torța. Aceste forme se numesc secțiuni conice și sunt curbele pe care le obțineți dacă tăiați un con la diferite unghiuri diferite. Tocmai aceste curbe au fost studiate de greci, care au recunoscut că existau în principiu patru tipuri de secțiuni conice. Dacă se ia o secțiune orizontală prin con, se obține un cerc. O secțiune la un unghi mic față de orizontală vă oferă o elipsă. Dacă se ia o secțiune verticală, se obține o hiperbolă, iar dacă se ia o secțiune paralelă cu o latură a conului, se obține o parabolă. Aceste curbe sunt ilustrate mai jos.
 |
 |
 |
 |
 |
 |
 |
 |

O cruce.secțiune transversală a unui con poate fi un cerc …. |

… o elipsă … |
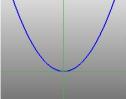
… o parabolă … |
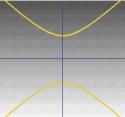
…. sau o hiperbolă. |
Secțiunile clonice intră în povestea noastră pentru că fiecare dintre ele este descrisă de o ecuație pătratică. În particular, dacă 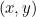 reprezintă un punct pe fiecare curbă, atunci o ecuație pătratică leagă
reprezintă un punct pe fiecare curbă, atunci o ecuație pătratică leagă  și
și 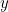 . Avem:
. Avem:
Cercul: 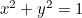 ;
;
Elipsa: 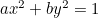 ;
;
Hiperbola: 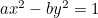 ;
;
Parabola: 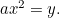
Aceste curbe erau cunoscute și studiate încă de la greci, dar, în afară de cerc, ele nu păreau să aibă nicio aplicație practică. Cu toate acestea, după cum vom vedea în următorul număr al revistei Plus, o legătură între ecuațiile pătratice și conice, împreună cu o întâmplare extrem de norocoasă, a dus la o înțelegere a modului în care funcționa universul, iar în secolul al XVI-lea a venit momentul în care conicele au schimbat lumea.
Despre autori
Chris Budd este profesor de matematică aplicată în cadrul Departamentului de Științe Matematice de la Universitatea din Bath și președinte al Catedrei de Matematică de la Royal Institution din Londra.
Chris Sangwin este membru al personalului de la Școala de Matematică și Statistică de la Universitatea din Birmingham. Este cercetător în cadrul centrului Learning and Teaching Support Network pentru matematică, statistică și cercetare operațională.
Aceștia au scris recent cartea de matematică populară Mathematics Galore!, publicată de Oxford University Press.
Acest articol a fost inspirat în parte de o dezbatere remarcabilă din Camera Comunelor din Marea Britanie pe tema ecuațiilor pătratice. Înregistrarea acestei dezbateri poate fi găsită în Hansard, Camera Comunelor din Regatul Unit, 26 iunie 2003, coloanele 1259-1269, 2003, care este disponibilă online pe site-ul House of Commons Hansard Debate.