Elevă de clasa a patra Alice întreabă: „Câte diagonale sunt în decagon?”
Bună întrebare, Alice. Dar, în loc să-ți dau un răspuns la această întrebare, am să-ți arăt cum poți să-ți dai seama singur. Și nu numai atât, îți voi arăta cum poți afla răspunsul pentru orice poligon, chiar dacă acesta are 20, sau 50, sau 2000 de laturi!
Pregătită? Să începem cu un exemplu simplu. Vom merge cu un poligon care are 8 laturi (care se numește octogon), așa:
Acum, acest poligon, pentru că are opt laturi, are și opt vârfuri. Pare un pic copleșitor să încercăm să ne dăm seama de toate diagonalele, așa că hai să ne concentrăm doar pe un singur vârf. Câte diagonale puteți desena într-un octogon, care să înceapă toate de la un singur vârf?
Răspunsul la această întrebare este cinci. Aruncați o privire la diagrama de mai jos:

În această diagramă am ales diagonala din stânga, chiar sub vertexul de sus, și am trasat diagonale la fiecare vertex la care pot trasa o diagonală. Către ce diagonale nu pot să desenez diagonale? Ei bine, nu pot desena o diagonală de la un vârf înapoi la el însuși și nu pot desena diagonale către cele două vârfuri de lângă acesta (pentru că acestea nu ar fi diagonale; ar fi laturi!).
Deci există trei vârfuri către care nu pot desena diagonale din acel vârf. Opt vârfuri în total, minus cele trei spre care nu pot desena, rămân cinci. Este important de reținut: scădeți 3 din numărul de vârfuri și veți avea numărul de diagonale pe care le puteți trasa de la orice vârf.
Dar acesta este doar un singur vârf! Ai putea desena diagonale din orice vertex, nu? Sigur că da! Și sunt opt vârfuri în octogonul nostru, așa că luăm numărul de diagonale pe vertex și îl înmulțim cu numărul de vârfuri: 5 x 8 = 40.
Ați putea fi tentați să credeți că acesta este răspunsul nostru, dar nu este așa. De ce nu? Pentru că am numărat fiecare diagonală de două ori! Fiecare diagonală are două vârfuri, așa că am numărat-o de la un capăt și am numărat-o și de la celălalt capăt. Deci, pentru a obține numărul real de diagonale, trebuie să împărțim răspunsul nostru la 2. 40 / 2 = 20. Există douăzeci de diagonale într-un octogon.
Să încercăm acest raționament pe un poligon care are 2000 de laturi. Acum, nu am de gând să vă desenez un poligon cu 2000 de laturi; va trebui să rezolvăm raționamentul fără o imagine.
- Alegeți un vârf. Câte diagonale puteți trasa de la acel vertex? Răspuns: 2000 – 3 = 1997.
- Câte vârfuri în total? Răspuns: 2000
- Câte diagonale s-au numărat din toate vârfurile? Răspuns:: 1997 x 2000 = 3.994.000
- Oops! Am numărat fiecare diagonală de două ori! Cum scăpăm de cele duble? Răspuns: 3994000 / 2 = 1,997,000
Atunci, un 2000-gon are 1,997,000 de diagonale!
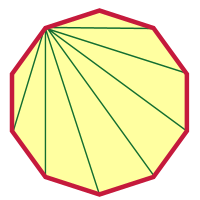
După ce am făcut ceva atât de nebunesc ca un 2000-gon, un decagon nu ar trebui să pară atât de dificil, nu? O să încep eu, iar tu poți termina de aici. Am ales un vertex și am trasat diagonale din acel vertex.
Câte sunt? Ai reușit să-ți dai seama câte sunt fără să te uiți la imagine?
Poți să-ți dai seama de aici? Sper că da! Mult noroc, Alice.
Apropo, există o formulă pe care o poți folosi; ea arată așa: D = n(n – 3)/2. Dar, sincer, nu mă aștept ca elevii mei să o memoreze. Mă aștept ca ei să își amintească modul în care o raționăm aici. Dacă înțelegeți logica, este chiar mai bine decât să aveți o formulă!
.