The standard formula to find the determinant of a 3×3 matrix is a breakdown down of smaller 2×2 determinant problems which are very easy to handle. Se você precisar de uma atualização, veja minha outra lição sobre como encontrar o determinante de uma matriz 2×2. Suponha que nos seja dada uma matriz quadrada A onde,
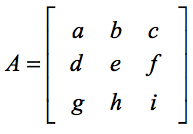
O determinante da matriz A é calculado como
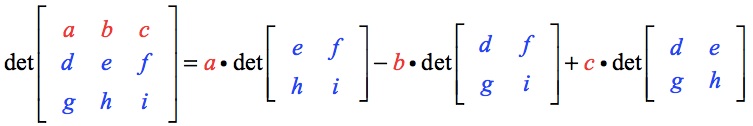
Aqui estão os pontos-chave:
- Note que os elementos da linha superior, nomeadamente a, b e c, servem como multiplicadores escalares para uma matriz 2 por 2 correspondente.
- A escalar a está sendo multiplicada para a matriz 2×2 de elementos remanescentes criados quando segmentos de linha verticais e horizontais são desenhados passando por a.
- O mesmo processo é aplicado para construir as matrizes 2×2 para multiplicadores escalares b e c.
Determinante de 3 x 3 Matriz (animada)

Exemplos de Como Encontrar o Determinante de uma Matriz 3×3
Exemplo 1: Encontre o determinante da matriz 3×3 abaixo.
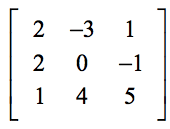
A configuração abaixo irá ajudá-lo a encontrar a correspondência entre os elementos genéricos da fórmula e os elementos do problema real.
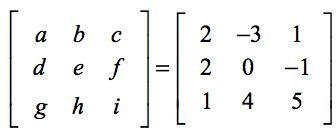
Aplicando a fórmula,


Exemplo 2: Avalie o determinante da matriz 3×3 abaixo.
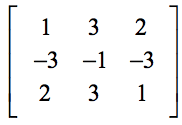
Seja muito cuidadoso ao substituir os valores nos lugares certos da fórmula. Erros comuns ocorrem quando os alunos se descuidam durante a etapa inicial de substituição de valores.
Além disso, tome seu tempo para certificar-se de que sua aritmética também esteja correta. Caso contrário, um único erro em algum lugar no cálculo produzirá uma resposta errada no final.
Desde,
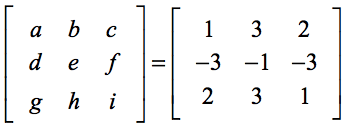
O nosso cálculo do determinante torna-se…

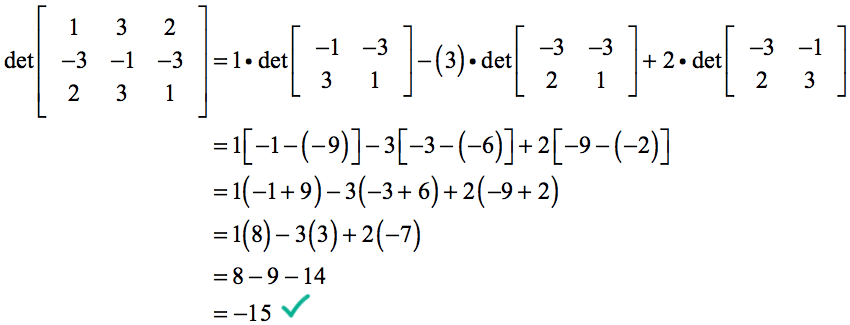
Exemplo 3: Resolva para o determinante da matriz 3×3 abaixo.
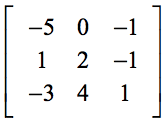
A presença de zero (0) na primeira linha deve tornar o nosso cálculo muito mais fácil. Lembre-se, esses elementos da primeira fila, atuam como multiplicadores escalares. Portanto, zero multiplicado por qualquer coisa fará com que toda a expressão desapareça.