Uma questão importante é: como os números primos estão distribuídos entre os números inteiros? A resposta é, em poucas palavras, de forma bastante aleatória, dadas certas estatísticas básicas…
 Bill Casselman
Bill Casselman
Universidade de British Columbia, Vancouver, Canadá
Email Bill Casselman
| |
|
Introdução
Muitos anos atrás foi conjeturado que há um número infinito de pares de números primos $p$, $q$ com $q = p+2$. Tem havido algum progresso recente (e famoso) sobre este problema. Eu direi pouco sobre os progressos recentes, mas discutirei em vez disso o que esperamos – tempo do que sabemos – sobre esses pares. Nada que eu direi é novo, e até certo ponto eu tenho meramente elaborado sobre o que Andrew Granville diz em sua recente nota expositiva sobre os avanços recentes.
Quantos primes nós esperamos?
Um número primo é um inteiro positivo que não tem divisores a não ser ele mesmo e $1$. A definição é simples, mas assim que se começa a explorar o significado dos números primos, percebe-se que eles exibem um comportamento muito sutil. Uma questão importante é, como os números primos são distribuídos entre os números inteiros? A resposta é, em poucas palavras, de forma bastante aleatória, dadas certas estatísticas básicas. O que quero dizer com isto?
Bem, aqui está um array quadrado que retrata todos os primes até $400$:

Existem alguns padrões neste array, alguns dos quais vou comentar mais tarde. A maioria dos que você percebe são causados por algum artefato do display. Por exemplo, todas as outras colunas estão essencialmente vazias, e isto é porque o único prime é $2$. Além disso, cada quinta coluna está essencialmente vazia. Mais interessantes são os pares twin prime (alguns dos quais não são tão visíveis porque se dividem em duas linhas, tais como $59$, $61$), e também alguns padrões relacionados com os últimos dígitos exibidos. Estes são o que pode ser chamado de padrões locais. Não existem padrões globais aparentes.
Há muito esforço colocado em formas extremamente eficientes de produzir números primos, mas hoje em dia até mesmo um programa muito simples leva apenas uma pequena quantidade de tempo para fazer grandes listas de primes. Um dos programas mais frutíferos irá fazer uma grande lista de primes e depois usar isto para calcular a função $\pi(n)$, o número de primes $\le n$.
Uma coisa que pode ser usada é para ter uma ideia aproximada da frequência dos primes. Há $135$ primes na faixa de $$:
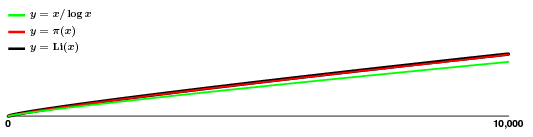
A aproximação parece ótima! Então, mesmo que $\pi(x)$ salte um pouco, aparentemente sem muito padrão, temos uma estimativa bastante boa, o que significa que temos uma boa idéia de como os primes crescem, pelo menos na média.
Deve-se ter em mente, no entanto, que a aparente suavidade é enganadora. De perto, aqui está o aspecto das duas curvas superiores:

Comentários?
Relação heurística sobre os primes gêmeos
Primes gêmeos são um par $p$, $p+2$ que são ambos primes. Por exemplo, de um dos gráficos acima vemos os twin primes $$ , , , , , , , $$
e outros. Tem sido conjeturado que há um número infinito deles, mas embora haja muitas evidências empíricas para isso, ainda não foi provado.
Talvez a evidência mais forte é uma fórmula que se aproxima do número $\pi_{2}(x)$ de primes gêmeos $\le x$ notavelmente bem. Não tenho certeza sobre a origem desta fórmula, mas ela apareceu pela primeira vez em um artigo de G. H. Hardy e J. E. Littlewood (eles mesmos um par de primes gêmeos) datado de 1923. O artigo contém várias fórmulas semelhantes, todas baseadas no mesmo método, que eles tinham usado para atacar muitos problemas anteriormente. Este era o método circular deles. A sua derivação da fórmula para $\pi_{2}(x)$ não é de todo rigorosa, mas é muito convincente. Há um relato sucinto disso em um apêndice do artigo de Andrew Granville.
Mas logo após a Segunda Guerra Mundial Lord Cherwell (Frederick Lindemann) sugeriu uma derivação probabilística (e ainda não rigorosa) mais elementar. Isto levou a uma colaboração com E. M. Wright e eventualmente a uma publicação conjunta póstumo. Isto é explicado na Secção 22.20 do conhecido texto de Hardy e Wright. Uma versão um pouco mais elementar pode também ser encontrada num apêndice do artigo de Granville (Secção 2.5). Eu o sigo.
O ponto de partida para o raciocínio plausível é nossa estimativa de $\pi(x)$, o número de primes menor ou igual a $x$. A idéia básica da derivação é que os números primos estão, em boa medida, distribuídos aleatoriamente. Sabemos que na vizinhança de $x$ a densidade de primes é de cerca de $1/\\log x$. Se os primes fossem distribuídos aleatoriamente, então a probabilidade de que quaisquer dois números dados próximos de $x$ sejam primes seria então apenas o produto de probabilidades locais, que é $1/\log^{2} x$. Isto certamente é um raciocínio ilusório, pois se $n > 2$ a probabilidade de ambos $n$ e $n+1$ serem primes é $0$, enquanto o fato de $p$ ser um primes parece aumentar as chances de que $p+2$ seja. Há considerações semelhantes a ter em conta devido à possível divisibilidade por outros primes pequenos, também, na vizinhança de $x$.
Existe um facto simples nesta história. Se $q$ é qualquer prim, então a probabilidade de escolher um inteiro ao acaso que não seja divisível por $q$ é de $1-1/q$. A probabilidade de escolher dois que não sejam divisíveis por $q$ é portanto o produto $(1 – 1/q)^{2}$. Suponha que $p$ e $p+2$ são ambos primes, então nem $p$ nem $p+2$ são divisíveis por $q$. Se $q = 2$, isto acontece $1/2$ o tempo. Se $q = 2$, a probabilidade de que $p nãoequiv 0$ e $p nãoequiv -2$ modulo $q$ é $(1 – 2/q)$. Devido ao Teorema do Restante Chinês, a divisibilidade por dois primes é um evento independente. Então se $x$ é grande e $Q$ é relativamente pequeno a probabilidade de que qualquer par de números $m$ e $n$ perto de $x$ não será um múltiplo de qualquer primes até $Q$ é $$$$$ (1 sobre 2). { (1 – 1/q)^{2} } \. $$693>
Let $ $\Gamma_{Q}$ ser a razão disto para $\d_{q}le Q}(1 – 2/q)$: $$$Gamma_{Q} = $$ 1 acima de 2}cdot {q}prod_{q}le Q { (1 – 1/q)^{2} \(1 – 2/q) $$ Nós temos $$ { 1 – 2/q (1-1/q)^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \sobre (1 – 1/q)^{2} } = 1 – { 1 ^ (q -1)^{2} } \. $$ Um critério padrão afirma que este produto converge se a soma de $$ 1/(q-1)^{2}$ converge. Mas ele converge, uma vez que o teste integral nos diz que $$$ 1/n^{2}$ converge. Portanto, este produto realmente converge para um número $\Pi_{\i}$ como $Q {\i}rightarrow {\i}$. Que $C_{2}$ seja o seu inverso. A secção 2.5 do artigo de Granville diz que deve ser intuitivamente razoável neste ponto que o número $\pi_{2}(x)$ de primários gémeos $\pi_{2}(x)$ seja aproximado por $$\pi_{2}(x) = C_{2}. \Não sei… “dx” no log… \. $$
O texto de Hardy and Wright apresenta uma análise mais cuidadosa que torna o salto intuitivo um pouco mais claro.
O valor da constante aqui foi calculado há muito tempo por J. W. W. Wrench para ser cerca de $1.32032363169373914785562422002911155686525 \ldots $. Aqui está uma comparação de alguns valores de $\pi_{2}(x)$ e a fórmula na faixa $$: $$ \matrix{ n & 10,000 & 20,000 & 30,000 & 40,000 & 50,000 \pi_{2}(n) & 205\phantom{.0} & 342 {.0}phantom{.0} & 467 {.0}phantom{.0} & 591 {.0}phantom{.0} & 705 {.0}phantom{.0} & \i_{.2}(x) & 214.2 & 357.7 & 486.7 & 607.4 & 72213.5 \i_{.0} $$ $$ \matrix{ n & 60,000 & 70,000 & 80,000 & 90,000 & 100,000 \pi_{2}(n) & 811 \i_{.0} & 905 {.0}phantom{.0} & 1007 {.0}phantom{.0} & 1116 {.0}phantom{.0} & 1224 {.0}phantom{.0} \{.0}cr \i_{.2}(x) & 833.3 & 940.9 & 1045.7 & 1148.2 & 1248.7 \i_cr } $$
Comentários?
Conjecturas do Dickson
Primeiro dewin são um caso especial de algo muito mais geral. Pode-se perguntar, há um número infinito de pares $p$, $p+4$ ou $p$, $p+6$ que são primes? Ou $p$, $p+10$? O caso de $p$ e $p+10$ é certamente sugerido por uma das imagens acima, em que tais pares são facilmente visíveis. Que tal triplos de algum tipo? Suponha que $a_{1}$, $a_{2}$, $\ldots$ , $a_{k}$ compõem um array de inteiros. Podemos esperar que haja um número infinito de conjuntos $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$ todos os quais são prime?
Um tem que ser um pouco cuidadoso. Não há pares prime da forma $p$, $p+1$ (passado $p = 2$), porque um destes dois números deve ser divisível por $2$. Da mesma forma, passado $p = 3$ não há triplos primos $p$, $p+2$, $p+4$ porque um destes tem de ser divisível por $3$.
Este último exemplo deve ser esclarecedor. O número $p+4$ é divisível por $3$ se e somente se $p+1$ for divisível por $3$. Portanto $3$ divide um dos números $p$, $p+2$, $p+4$ se e somente se dividir $p$, $p+1$, $p+2$. Mas isto certamente acontecerá, já que o último triplo cobre claramente todos os números modulo $3$.
Em geral, $p$ é dito ser uma obstrução para o array $(a_{i})$ se $p$ sempre divide pelo menos uma de cada seqüência $n+a_{i}$ ($i = 1$, $\ldots$, $k$). Isto acontece se e somente se os números $a_{i} \Mod… \p$ encher tudo de $Z/p$.
Isto nunca pode acontecer se $p > k$, então para verificar se algum $p$ obstrui $(a_{i})$ só precisamos verificar se o $a_{i}$ cobre $Z/p$ para todos os $p {le k$. Nós chamamos o array de $(a_{i})$ admissível se ele não tiver nenhuma obstrução principal.
Por exemplo, $(1,3,7,9)$ é um array admissível, uma vez que, como você pode verificar facilmente, nem $2$ nem $3$ é uma obstrução. Várias seqüências principais que se encaixam neste padrão podem ser vistas em um dos diagramas acima. Outros exemplos são (a) qualquer $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
Existem arbitrariamente grandes conjuntos admissíveis. Na verdade:
Teorema. Se $a_{1}$ a $a_{k}$ é qualquer conjunto de primes distintos $> k$, eles compõem um conjunto admissível.
Porquê isto? Se $p$ é qualquer primes onde $p> k$, então nós já vimos que não pode ser uma obstrução. Mas se $p \le k$, então não pode dividir nenhum dos $a_{i}$, nenhum dos quais pode ser congruente com $0$ modulo $p$. Então o $a_{i}$ não preenche $Z/p$.
Um caso especial de uma conjectura feita originalmente por L. E. Dickson é que se não há obstruções principais a $(a_{i})$ então existe um número infinito de sequências principais da forma $(n +a_{i})$.
O que aconteceu recentemente
Este não é o lugar para contar toda a história, que foi completamente coberta em outros lugares. Eu recomendo particularmente o artigo Quanta de Erica Klarreich para um relato popular, e o ensaio de Granville para um mais técnico. Eu só quero dizer um pouco mais precisamente do que no relato de Klarreich qual é o mais famoso dos novos resultados.
É devido a Yitang Zhang. A afirmação mais simples do que ele provou é que existe um número infinito de intervalos $[n, n+70.000.000)$ contendo pelo menos dois primes. Isto é mais fraco do que a conjectura de dois primes, mas conceitualmente muito próximo a ele. No trabalho subsequente (por muitos matemáticos) o tamanho do intervalo foi severamente reduzido, mas presumivelmente não há maneira de reduzi-lo para $2$ com os métodos atuais.
Como explicado por Granville, o primeiro de Zhang e sem dúvida seu principal resultado é que existe $k$ com a propriedade que se $a_{1}$, $\ldots$ , $a_{k}$ é um conjunto admissível de elementos $k$, então existe um número infinito de $n$ tal que $\i_{ n +a_{i} \$ contém pelo menos dois primes. (No artigo Quanta de Klarreich, a matriz é chamada de “pente.” Tenha em mente que, de acordo com a conjectura do Dickson, poderíamos dizer que todos os $k$ são primes). Na verdade, Zhang provou que esta afirmação é verdadeira para um determinado $k =3.500.000$, abrangendo um intervalo de $70.000.000$. A consequência por agora famosa é para cerca de $m \lt 70.000.000$ que existe um número infinito de pares primos $p$, $p+m$.
Ler mais adiante
- Lord Cherwell e E. M. Wright, “The frequency of prime patterns”, The Quarterly Journal of Mathematics 11 (1960).
Aqueles que conhecem algo da vida de Lord Cherwell, também conhecido como Frederick Lindemann, ficarão muito surpreendidos ao saber da sua contribuição para a teoria dos números. A biografia da Wikipédia não sugere adequadamente todas as razões para sua má reputação como principal conselheiro científico de Churchill durante a Segunda Guerra Mundial.
- L. E. Dickson, “A new extension of Dirichlet’s theorem on prime numbers”, Messenger of Mathematics 33.
Veja também a entrada da Wikipédia sobre a conjectura de Dickson.
- Andrew Granville, “Primes in intervals of bounded length” (Primes em intervalos de comprimento limitado). Disponível na sua página inicial.
- G. H. Hardy, Ramanujan, Cambridge University Press.
Secção 2.5 contém uma derivação ideal de uma possível fórmula para $\pi(x)$.
- G. H. Hardy e J. E. Littlewood, “Some problems of ‘Partitio numerorum’ III: on the expression of a number as a sum of primes”, Acta Mathematica 44 (1923).
- G. H. Hardy e E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, “Together and alone, closing the prime gap”, Quanta 19 de Novembro de 2013.
- B. Riemann, “Sobre o número de números primos inferior a uma determinada quantidade”. Uma tradução inglesa deste clássico de David Wilkins está disponível a partir de um link na Wikipedia.
entre outras coisas, este esboça uma derivação da fórmula aproximada para $\pi(x)$.
- J. W. Wrench, “Evaluation of Artin’s constant and the twin-prime constant”, Mathematics of Computation 76 (1961).
Um cálculo inicial de $C_{2}$.
- Listas de primes até $1.000.000.000.000$
- Uma lista dos primeiros 20.000 primes gêmeos.
 Bill Casselman
Bill Casselman
Universidade de British Columbia, Vancouver, Canadá
Email Bill Casselman