Quatro graus Alice pergunta, “Quantas diagonais estão em decágono?”
Grande pergunta, Alice. Mas em vez de lhe dar uma resposta a essa pergunta, vou lhe mostrar como você pode descobrir por si mesma. E não só isso, vou mostrar-te como podes descobrir a resposta para qualquer polígono, mesmo que tenha 20, ou 50, ou 2000 lados!
Pronto? Vamos começar com um exemplo simples. Vamos com um polígono que tem 8 lados (que é chamado de octógono), como este:
Agora, este polígono, porque tem oito lados, também tem oito vértices. Parece um pouco avassalador tentar perceber todas as diagonais, então vamos focar apenas em um vértice. Quantas diagonais você pode desenhar em um octógono, que começam todas em um vértice?
A resposta a essa pergunta é cinco. Dê uma olhada no diagrama abaixo:

Neste diagrama eu escolhi a diagonal para a esquerda logo abaixo do vértice superior, e eu desenhei diagonais para cada vértice em que eu posso desenhar uma diagonal. Para quais diagonais eu não posso desenhar diagonais? Bem, eu não posso desenhar uma diagonal de um vértice para si mesmo, e eu não posso desenhar diagonais para os dois vértices ao lado daquele (porque aquelas não seriam diagonais; elas seriam laterais!).
Então existem três vértices para os quais eu não posso desenhar diagonais a partir daquele vértice. Oito vértices no total, menos os três para os quais não consigo desenhar, deixa cinco. Isso é importante lembrar: subtraia 3 do número de vértices, e você tem o número de diagonais que pode desenhar de qualquer vértice.
Mas isso é apenas um vértice! Você pode desenhar diagonais a partir de qualquer vértice, certo? Claro que sim! E há oito vértices em nosso octógono, então pegamos o número de diagonais por vértice, e o multiplicamos pelo número de vértices: 5 x 8 = 40.
Podes ser tentado a pensar que essa é a nossa resposta, mas não é. Por que não? Porque já contamos cada diagonal duas vezes! Cada diagonal tem dois vértices, por isso contámo-la de uma ponta, e também a contámos da outra ponta. Então para obter o número real de diagonais, temos de dividir a nossa resposta por 2. 40 / 2 = 20. Há vinte diagonais num octógono.
Vamos tentar esse raciocínio num polígono que tem 2000 lados. Agora, eu não vou desenhar um 2000-gon para você; só temos que trabalhar o raciocínio sem uma figura.
- Pick a vértice. Quantas diagonais você pode desenhar a partir desse vértice? Resposta: 2000 – 3 = 1997.
- Quantos vértices totalizam? Resposta: 2000
- Quantas diagonais contam-se de todos os vértices? Resposta: 1997 x 2000 = 3.994.000
- Oops! Nós contamos cada diagonal duas vezes! Como é que nos livramos das duplicatas? Responda: 3994000 / 2 = 1.997.000
Então um 2000-gon tem 1.997.000 diagonais!
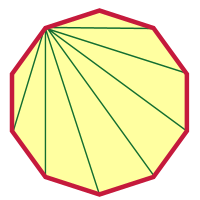
Depois de fazer algo tão louco como um 2000-gon, um decagon não deve parecer tão difícil, certo? Vou começar, e podes terminá-lo a partir daqui. Escolhi um vértice e tirei diagonais desse vértice.
Quantos são? Conseguiste perceber quantas eram sem olhar para a imagem?
Pode descobrir a partir daqui? Eu espero que sim! Boa sorte, Alice.
Por falar nisso, há uma fórmula que podes usar; é parecida com esta: D = n(n – 3)/2. Mas honestamente, não espero que os meus alunos a memorizem. Eu espero que eles se lembrem de como nós a raciocinamos aqui. Se você entender a lógica, é ainda melhor do que ter uma fórmula!