Modelagem matemática

by admin Leave Comment

Objectivos de aprendizagem

  • Introdução às funções por etapas
    • Definir por etapas função
    • Avalie uma função por troços
    • Escreva uma função por troços dada uma aplicação
  • Funções por troços
    • Dado um troço…função definida, esboçar um gráfico
    • Escrever o domínio e o alcance de uma função por partes dado um gráfico

Algumas funções vêm em pedaços. Nesta secção, aprenderemos como definir e fazer gráficos de funções que são essencialmente colecções de peças discretas. Exemplos de algo definido desta forma incluem o desenho do perfil de um carro, o desenho do plano do seu telemóvel, e o cálculo das taxas de imposto de renda. Por exemplo, a sua taxa de imposto depende dos seus rendimentos e é a mesma para uma série de rendimentos, como se pode ver na tabela abaixo:

Taxa de imposto marginal Renda única tributável Arquivo conjugado ou Viúva(er) Qualificada(s) tributável Rendimento Arquivamento Casado Separadamente Rendimento Tributável Chefe do Rendimento Tributável Familiar
10% $0 – $9,275 $0 – $18,550 $0 – $9,275 $0 – $13,250
15% $9,276 – $37,650 $18,551 – $75,300 $9,276 – $37,650 $13,251 – $50,400
25% $37,651 – $91,150 $75,301 – $151,900 $37,651 – $75,950 $50,401 – $130,150
28% $91,151 – $190,150 $151,901 – $231,450 $75,951 – $115,725 $130,151 – $210,800
33% $190,151 – $413,350 $231,451 – $413,350 $115,726 – $206,675 $210,801 – $413,350
35% $413,351 – $415,050 $413,351 – $466,950 $206,676 – $233,475 $413,351 – $441,000
39.6% $415.051+ $466.951+ $233.476+ $441.001+

Uma função por partes é uma função na qual mais de uma fórmula é usada para definir a saída em diferentes partes do domínio.

Usamos funções compostas para descrever situações em que uma regra ou relação muda à medida que o valor de entrada atravessa certos “limites”. Por exemplo, encontramos frequentemente situações nos negócios para as quais o custo por peça de um determinado item é descontado quando o número encomendado excede um determinado valor. Os escalões de imposto são outro exemplo do mundo real de funções por partes. Por exemplo, considere um sistema de impostos simples no qual rendimentos até $10.000 são tributados a 10%, e qualquer rendimento adicional é tributado a 20%. O imposto sobre um rendimento total, S, seria 0,1S se S\le $10.000 e 1000 + 0,2 (S – $10.000), se S> $10.000,

Função por Via Económica

Função por Via Económica é uma função em que mais de uma fórmula é usada para definir a saída. Cada fórmula tem o seu próprio domínio, e o domínio da função é a união de todos esses domínios menores. Notamos esta ideia desta forma:

f\i>esquerda(x)=begin{cases}{fórmula 1 se x estiver no domínio 1}} \i>texto{fórmula 2 se x estiver no domínio 2} \i>texto{fórmula 3 se x estiver no domínio 3}end{cases}

Em notação por método combinado, a função de valor absoluto é

|x|=\begin{cases}x\text{ if }x\ge 0\ -x\text{ if }x<0\end{cases}

Avalie uma função definida por método combinado

No primeiro exemplo, mostraremos como avaliar uma função definida por método combinado. Observe como é importante prestar atenção ao domínio para determinar qual expressão usar para avaliar o input.

Exemplo

Dar a função

f(x)=\begin{cases}7x+3\text{ if }x<0\7x+6\text{ if }x^^ge{0},

avaliar:

  1. f (-1)
  2. f (0)
  3. f (2)
Mostrar Resposta

1.f(x) é definido como 7x+3 para x=-1\text{ becuase }-1<0.

Evalue: f(-1)=7(-1)+3=-7+3=-4

2. f(x) é definido como 7x+6 para x=0\text{ becuase }0\ge{0}.

Evaluate: f(0)=7(0)+6=0+6=6

3. f(x) é definido como 7x+6 para x=2\text{ becuase }2\ge{0}.

Avalie: f(2)=7(2)+6=14+6=20

No vídeo a seguir mostramos como avaliar vários valores dada uma função definida por partes.

No próximo exemplo mostramos como avaliar uma função que modela o custo de transferência de dados para uma empresa de telefonia.

Exemplo

Uma empresa de telefonia celular usa a função abaixo para determinar o custo, C, em dólares para g gigabytes de transferência de dados.

>

C{esquerda(g}{direita)={casos}{25}{texto{ se }{ 0 }<{ g }<{ 2 }{ 10g+5}texto{ se }{ g}ge{ 2 }end{casos}

Cobrir o custo do uso de 1.5 gigabytes de dados e o custo de usar 4 gigabytes de dados.

Mostrar Resposta

Para encontrar o custo de usar 1.5 gigabytes de dados, C(1.5), primeiro olhamos para ver em que parte do domínio a nossa entrada cai. Como 1.5 é menor que 2, usamos a primeira fórmula.

C(1.5) = $25

Para encontrar o custo de usar 4 gigabytes de dados, C(4), vemos que nosso input de 4 é maior que 2, então usamos a segunda fórmula.

C(4)=10(4)+5=45

Análise da solução

A função está representada no gráfico abaixo. Podemos ver onde a função muda de uma constante para uma linha com uma inclinação positiva em g=2. Traçamos os gráficos para as diferentes fórmulas em um conjunto comum de eixos, assegurando que cada fórmula seja aplicada em seu próprio domínio.

C(g) = C\esquerda(g\direita)={cases}{25}{25}{texto{ if }{ 0 }<{ g }<{ 2 }{ 10g+5}texto{ if }{ g}ge{ 2 }end{cases}

Escreva uma Função Definida por Objectos

No último exemplo mostraremos como escrever uma função definida por Objectos que modele o preço de uma visita guiada ao museu.

Exemplo

Um museu cobra $5 por pessoa para uma visita guiada com um grupo de 1 a 9 pessoas ou uma taxa fixa de $50 para um grupo de 10 ou mais pessoas. Escreva uma função relacionando o número de pessoas, n, ao custo, C.

Mostrar Resposta

Duas diferentes fórmulas serão necessárias. Para n-valores inferiores a 10, C=5n. Para valores de n iguais ou superiores a 10, C=50.

C(n)=}begin{cases}{5n}{5n}}text{ if }{0}<{n}<{10}} 50{text{ if }{n}ge 10{cases}

Análise da Solução

A função é representada na Figura 21. O gráfico é uma linha diagonal de n=0 a n=10 e uma constante depois disso. Neste exemplo, as duas fórmulas estão de acordo no ponto de encontro onde n=10, mas nem todas as funções compostas têm esta propriedade.

No vídeo a seguir, mostramos um exemplo de como escrever uma função definida por tecnologia combinada dada uma situação.

Dada uma função combinada, escreva a fórmula e identifique o domínio para cada intervalo.

  1. Identificar os intervalos aos quais se aplicam regras diferentes.
  2. Determinar fórmulas que descrevem como calcular uma saída de uma entrada em cada intervalo.
  3. Utilizar chaves e if-statements para escrever a função.

Funções compostas por gráfico

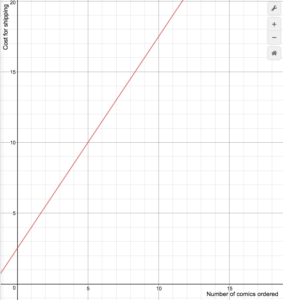
Nesta seção, plotaremos as funções compostas. A função plotada abaixo representa o custo de transferência de dados para uma determinada empresa de telefonia celular. Podemos ver onde a função muda de uma constante para uma linha com um declive positivo em g=2. Quando traçamos as funções por método combinado, é importante garantir que cada fórmula seja aplicada em seu próprio domínio.C\i(g\i(g\i(g\i(g\i(g\i(g)=)) \texto{ if }{ 0 }<{ g }<{ 2 }10g+5}text{ if }{ g}ge{ 2 }end{ 2 }end{cases}

Neste caso, a saída é 25 para qualquer entrada entre 0 e 2. Para valores iguais ou superiores a 2, o output é definido como 10g+5.

Dando uma função por partes, desenhe um gráfico.

  1. Indique no eixo x os limites definidos pelos intervalos em cada parte do domínio.
  2. Para cada parte do domínio, faça um gráfico nesse intervalo usando a equação correspondente a essa parte. Não faça um gráfico de duas funções em um intervalo porque isso violaria o critério de uma função.

Exemplo

Traçar um gráfico da função.

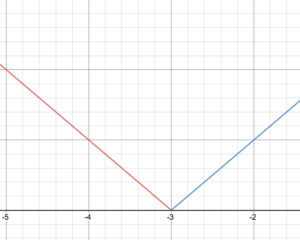
Dar a definição por segmentos f(x)=\begin{cases}-x – 3\text{ if }x < -3\\\ x + 3\text{ if } x \ge -3\end{cases}
Desenhar o gráfico de f.
Dizer o domínio e o alcance da função.

Mostrar Resposta

Primeiro, grafique a linha f(x) = -x-3, apagando a parte onde x é maior que -3. Coloque um círculo aberto em (-3,0).

Agora coloque a linha f(x) = x+3 no gráfico, começando no ponto (-3,0). Note que para esta parte do gráfico, o ponto (-3,0) está incluído, assim você pode remover o círculo aberto.

Os dois gráficos se encontram no ponto (-3,0)

O domínio desta função é todo números reais porque (-3,0)não está incluído como o ponto final de f(x) = -x-3, mas está incluído como o ponto final de f(x) = x+3.

O intervalo desta função começa em f(x)=0 e inclui 0, e vai até ao infinito, por isso escreveríamos isto como x\ge0

No próximo exemplo, vamos fazer um gráfico de uma função definida por partes que modela o custo de envio para um retalhista de banda desenhada online.

Exemplo

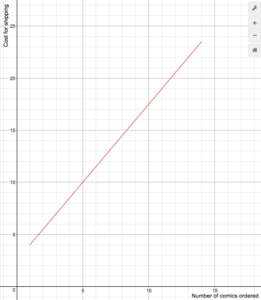
Um revendedor de banda desenhada on-line cobra os custos de envio de acordo com a seguinte fórmula

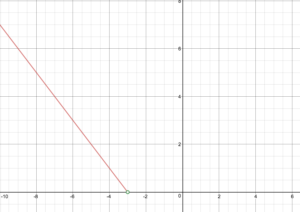
S(n)=\begin{cases}1.5n+2.5\text{ if }1\le{n}le14\0\text{ if }nge15\end{cases}

Desenhar um gráfico da função custo.

Mostrar resposta

Primeiro, desenhe a linha S(n)=1,5n+2,5. Podemos usar transformações: este é um trecho vertical da identidade por um fator de 1,5, e um deslocamento vertical por 2,5,

S(n)=1,5n+2.5

Agora podemos eliminar as porções do gráfico que não estão no domínio baseado em 1\le{n}\le14

>

S(n) = 1,5n+2,5 para 1<=n<=14

Próximo, adicione a função constante S(n)=0 para entradas maiores ou iguais a 15. Coloque pontos fechados nas extremidades do gráfico para indicar a inclusão dos pontos finais.

No vídeo a seguir mostramos como fazer o gráfico de uma função definida por partes, que é linear em ambos os domínios.

Resumo

  • Uma função por via combinada é uma função em que mais de uma fórmula é usada para definir a saída em diferentes partes do domínio.
  • Avaliar uma função por via combinada significa que você precisa prestar muita atenção à expressão correta usada para a entrada dada

Para fazer o gráfico de funções por via combinada, primeiro identifique onde o domínio está dividido. Gráficos de funções no domínio usando ferramentas como pontos de plotagem, ou transformações. Tenha cuidado para usar círculos abertos ou fechados nos pontos finais de cada domínio com base na inclusão ou não do ponto final.

Deixe uma resposta

O seu endereço de email não será publicado.