Metade Adição e Circuito de Verdade de Adição Completa
Circuitos de Meia Adição e Adição Completa é explicado com suas tabelas de verdade neste artigo. O design da Adder completa usando o circuito Half Adder também é mostrado. Circuito Adder Completo de um bit e adição Multi-bit usando o Adder Completo também é mostrado.
Antes de entrar neste assunto, é muito importante saber sobre Lógica Booleana e Portões Lógicos.
TAKE A LOOK : BOOLEAN LOGIC
TAKE A LOOK : LOGIC GATES
TAKE A LOOK : FLIP FLOPS
O que é um Adder?
Um Adder é um tipo de calculadora que é usada para adicionar dois números binários. Quando digo calculadora, não me refiro a uma com botões, esta é um circuito que pode ser integrado com muitos outros circuitos para uma vasta gama de aplicações. Existem dois tipos de adders;
- Metade adder
- Total adder
Metade adder
Com a ajuda da meia adder, podemos desenhar circuitos que são capazes de realizar adições simples com a ajuda de portas lógicas.
Vamos primeiro ver a adição de bits simples.
0+0 = 0
0+1 = 1
1+0 = 1
1+0 = 1
1+1 = 10
Estas são as combinações de bits simples menos possíveis. Mas o resultado para 1+1 é 10. Embora este problema possa ser resolvido com a ajuda de uma porta EXOR, se você se preocupar com a saída, o resultado da soma deve ser reescrito como uma saída de 2 bits.
Assim as equações acima podem ser escritas como
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
>Aqui a saída ‘1’de ’10’ torna-se a execução. O resultado é mostrado em uma tabela de verdades abaixo. A ‘SUM’ é a saída normal e a ‘CARRY’ é a execução.
INPUTS OUTPUTS
A SUM CARRY
0 0 0 0 0 0
0 1 1 1 0
1 0 1 0
1 1 0 1
Da equação, é claro que este adder de 1 bit pode ser facilmente implementado com a ajuda do EXOR Gate para a saída ‘SUM’ e um AND Gate para o transporte. Dê uma olhada na implementação abaixo.
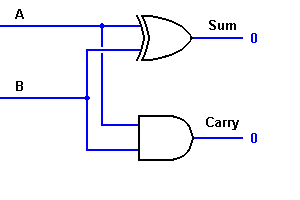
Para adição complexa, pode haver casos em que você tenha que adicionar dois bytes de 8 bits juntos. Isto só pode ser feito com a ajuda da lógica da bexiga completa.
Aplicador completo
Este tipo de aplicador é um pouco mais difícil de implementar do que uma meia bexiga. A principal diferença entre uma meia bexiga e uma bexiga cheia é que a bexiga cheia tem três entradas e duas saídas. As duas primeiras entradas são A e B e a terceira entrada é um input carry designado como CIN. Quando uma lógica de soma completa é projetada, nós seremos capazes de juntar oito delas para criar uma soma de bytes e em cascata o bit de transporte de uma soma para a próxima.
A saída de transporte é designada como COUT e a saída normal é designada como S. Dê uma olhada na tabela de verdades.
SAÍDAS DE ENTRADA
A B CIN COUT S
0 0 0 0 0 0 0
0 1 0 1
0 1 0 0 1
0 1 1 1 1 0
1 0 0 0 1
1 0 1 1 1 0
1 1 0 1 0 1 0
1 1 1 1 1 1 1 1
>
> da verdade acima.Mesa, a lógica completa do adder pode ser implementada. Podemos ver que a saída S é uma EXOR entre a entrada A e a saída SUM da meia bexiga com entradas B e CIN. Devemos também notar que a COUT só será verdadeira se alguma das duas entradas das três forem HIGH.
Thus, podemos implementar um circuito de adder completo com a ajuda de dois circuitos de meio adder. O primeiro será usado para adicionar A e B para produzir uma Soma parcial. A lógica da segunda metade adder pode ser usada para adicionar CIN à Soma produzida pela primeira metade adder para obter a saída S final. Se qualquer uma das lógicas de meia adição produzir um carry, haverá um carry de saída. Assim, COUT será uma função OR das saídas de transporte da meia bexiga. Dê uma olhada na implementação do circuito adder completo mostrado abaixo.
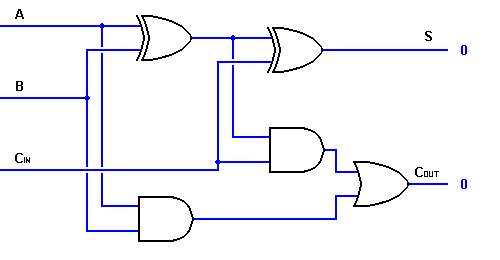
Embora a implementação de diagramas lógicos maiores seja possível com a lógica adder completa acima, um símbolo mais simples é usado principalmente para representar a operação. Dado abaixo é uma representação esquemática mais simples de uma Adder completa de um bit.
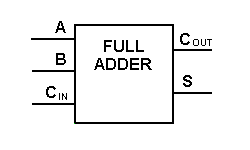
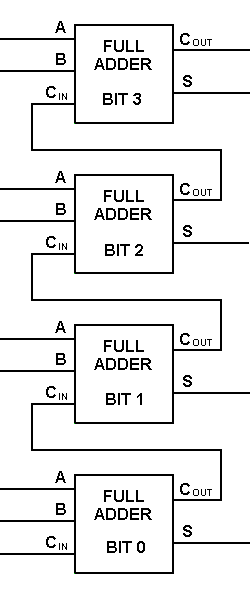
Com este tipo de símbolo, podemos adicionar dois bits juntos pegando um carry da próxima ordem inferior de magnitude, e enviando um carry para a próxima ordem superior de magnitude. Em um computador, para uma operação multi-bits, cada bit deve ser representado por um adder completo e deve ser adicionado simultaneamente. Assim, para adicionar dois números de 8 bits, você precisará de 8 vendedores completos que podem ser formados em cascata por dois dos blocos de 4 bits. A adição de dois números de 4 bits é mostrada abaixo.