Comecemos por examinar a divisão de valores com expoentes.
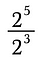
Recall exponents representam multiplicação repetida. Assim podemos reescrever a expressão acima como:
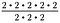
Desde 2/2 = 1, cancele três conjuntos de 2/2. Isto deixa 2 – 2, ou 2 ao quadrado.
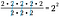
No curso podemos pegar um atalho e subtrair o número de 2’s na parte de baixo do número de 2’s na parte de cima. Como estas quantidades são representadas pelos seus respectivos expoentes, tudo o que precisamos fazer é escrever a base comum com a diferença nos valores dos expoentes como a potência.
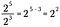
Se generalizarmos esta regra, temos o seguinte onde n representa um número real não-zero e x e y também são números reais.
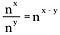
Explorar a potência zero
Daqui é fácil de derivar a explicação para que qualquer número não zero elevado à potência zero seja igual a 1. Novamente, vejamos um exemplo concreto.
Sabemos que qualquer número diferente de zero dividido por si mesmo é igual a 1. Então eu posso escrever o seguinte:
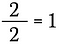
Isto é o mesmo que escrever:
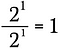
>
>
Agora vou utilizar a regra do expoente de cima para reescrever o lado esquerdo desta equação.
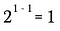
>
Of course, isto é equivalente a:
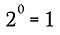
>
Podemos usar o mesmo processo como neste exemplo, juntamente com a regra generalizada acima, para mostrar que qualquer número real não-zero elevado à potência zero deve resultar em 1.
E que tal o zero para a potência zero?
É aqui que as coisas se complicam. O método acima quebra porque, é claro, dividir por zero é um não-não. Vamos examinar porquê.
Vamos começar por olhar para uma divisão comum por zero ERROR.
Que tal 2÷0? Vamos ver por que não podemos fazer isto.
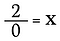
>
A divisão é realmente apenas uma forma de multiplicação, então o que acontece se eu reescrever a equação acima como:
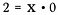
Que valor poderia satisfazer esta equação para x?
Não há valor! Qualquer número vezes zero resulta em zero, nunca pode ser igual a 2. Portanto, dizemos que a divisão por zero é indefinida. Não há solução possível.
Agora vamos olhar para 0÷0.
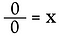
Again, reescreva-o como um problema de multiplicação.
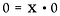
Aqui encontramos uma situação muito diferente. A solução para x poderia ser QUALQUER número real! Não há maneira de determinar o que é x. Portanto, 0/0 é considerado indeterminado*, não indefinido.
Se tentarmos usar o método acima com zero como base para determinar o que seria zero para a potência zero, nós paramos imediatamente e não podemos continuar porque sabemos que 0÷0 ≠ 1, mas é indeterminado.
Então o que faz com que zero para a potência zero seja igual?
Isto é altamente debatido. Alguns acreditam que deve ser definido como 1, enquanto outros pensam que é 0, e alguns acreditam que é indefinido. Existem bons argumentos matemáticos para cada um, e talvez seja mais corretamente considerado indeterminado.
Apesar disso, a comunidade matemática é a favor de definir zero para a potência zero como 1, pelo menos para a maioria dos fins.
Talvez uma definição útil de expoentes para o matemático amador seja a seguinte: