Não é frequente que uma equação matemática torne a imprensa nacional, muito menos popular na rádio, ou mais espantosamente, o tema de um debate no parlamento britânico. No entanto, em 2003 a boa e velha equação quadrática, que todos nós aprendemos na escola, foi tudo isso.
Onde começamos

Tudo começou numa reunião da União Nacional de Professores. A equação quadrática foi mantida no alto da nação como um exemplo da tortura cruel infligida pelos matemáticos às crianças pobres e insuspeitas da escola. Intrigada por esta acusação, a equação quadrática aceitou um papel de estrela na rádio em horário nobre, onde foi questionada por um entrevistador formidável mais acostumado a enfrentar o primeiro-ministro. O (London) Times tomou espaço na sua coluna líder, mais normalmente reservada a discussões de peso sobre a saúde moral (ou não) do mundo moderno, para proclamar que a equação quadrática era inútil, a matemática era inútil e que ninguém queria estudar matemática de qualquer maneira, então porquê incomodar-se. Preocupados para que as admissões perigosas pela equação quadrática não fossem contestadas, a importância vital da equação para a sobrevivência do Reino Unido foi debatida (uma visão positiva foi tomada, você pode ficar feliz em saber) na Câmara dos Comuns Britânica.
Onde tudo isso terminaria? Será que a equação quadrática estava realmente morta? Alguém se importou? Os matemáticos são monstros realmente malvados que só querem infligir equações quadráticas a uma geração mais jovem como meio de corromper suas almas imortais?
Talvez, mas não é realmente culpa da equação quadrática. Na verdade, a equação quadrática tem desempenhado um papel central não só em toda a civilização humana tal como a conhecemos, mas também na possível detecção de outras civilizações alienígenas e mesmo em actividades modernas tão vitais como ver televisão por satélite. O que mais, além da natureza da revelação divina, poderia ser considerado como tendo tido um tal impacto na vida tal como a conhecemos? De facto, num sentido muito real, as equações quadráticas podem salvar a sua vida.
Os Babilónios
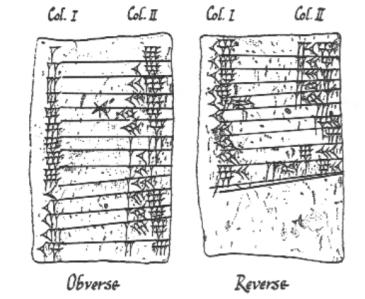
Os tabletes cuneiformes babilónicos que gravam as 9 vezes que as tabelas
Tudo começou por volta de 3000 a.C. com os Babilónios. Eles foram uma das primeiras civilizações do mundo, e surgiram com algumas grandes idéias como agricultura, irrigação e escrita. Eles traçaram os caminhos do Sol, da Lua e dos planetas, e gravaram-nos em tabuletas de barro (que ainda se pode ver no Museu Britânico). Aos babilônios devemos as idéias modernas de ângulo, incluindo a forma como o círculo é dividido em 360 graus (devido a um pequeno erro de cálculo, um por dia). Também devemos aos babilônios a invenção um pouco menos agradável do (temido) taxista. E esta foi uma das razões pelas quais os babilônios precisavam resolver equações quadráticas.
Vamos supor que você é um fazendeiro babilônico. Em algum lugar da sua fazenda você tem um campo quadrado no qual você cultiva alguma colheita. Que quantidade da sua colheita você pode cultivar no campo? O dobro do comprimento de cada lado do campo e você descobre que você pode cultivar quatro vezes mais do que antes. A razão para isto é que a quantidade da colheita que você pode cultivar é proporcional à área do campo, que por sua vez é proporcional ao quadrado do comprimento do lado. Em termos matemáticos, se  é o comprimento do lado do campo,
é o comprimento do lado do campo, 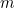 é a quantidade de colheita que pode crescer num campo quadrado de comprimento lateral 1, e
é a quantidade de colheita que pode crescer num campo quadrado de comprimento lateral 1, e  é a quantidade de colheita que pode crescer, então
é a quantidade de colheita que pode crescer, então
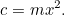 |
Esta é a nossa primeira equação quadrática, nua e piscando à luz do sol. Equações e áreas quadráticas estão ligadas entre si como irmãos e irmãs na mesma família. No entanto, no momento não temos que resolver nada – até que o homem dos impostos chegue, isto é! Alegremente ele diz ao agricultor “Quero que você me dê colheitas para pagar os impostos da sua fazenda”. O fazendeiro agora tem um dilema: de que tamanho um campo ele precisa para cultivar essa quantidade de colheita? Podemos responder facilmente a esta pergunta, de facto
colheitas para pagar os impostos da sua fazenda”. O fazendeiro agora tem um dilema: de que tamanho um campo ele precisa para cultivar essa quantidade de colheita? Podemos responder facilmente a esta pergunta, de facto
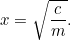 |
Encontrar raízes quadradas usando uma calculadora é fácil para nós, mas foi mais um problema para os babilónios. Na verdade eles desenvolveram um método de aproximação sucessiva à resposta que é idêntico ao algoritmo (chamado método Newton-Raphson) usado pelos computadores modernos para resolver problemas muito mais difíceis do que as equações quadráticas.
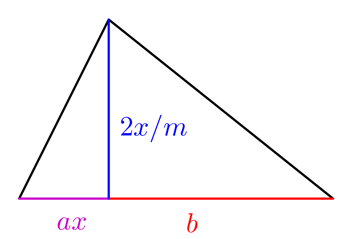
Agora, nem todos os campos são quadrados. Vamos agora supor que o agricultor tem um campo de forma mais estranha com duas secções triangulares, como mostra a direita.
Para valores apropriados de  e
e 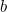 a quantidade de cultura que o agricultor pode cultivar neste campo é dada por
a quantidade de cultura que o agricultor pode cultivar neste campo é dada por
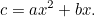 |
Isto parece-se muito mais com a equação quadrática a que estamos acostumados, e mesmo sob o mau olhado do homem dos impostos, é muito mais difícil de resolver. No entanto, os babilónios voltaram a ter a resposta. Primeiro dividimos por  para dar
para dar
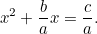 |
Agora completamos o quadrado usando o fato de que
Combinando isto com a equação original temos
>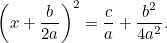
|
Esta é agora uma equação que podemos resolver tomando raízes quadradas. O resultado é a famosa “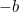 fórmula”:
fórmula”:
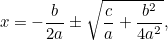 |
que pode ser reescrita como
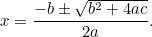 |
(A fórmula geralmente tem “-4ac” porque a equação quadrática é mais normalmente escrita na forma “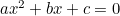 “.)
“.)
O facto de que tirar uma raiz quadrada pode dar uma resposta positiva ou negativa leva ao resultado notável de que uma equação quadrática tem duas soluções. Lá se vão os puzzles matemáticos tendo apenas uma solução!
Agora, é aqui que o ensino das equações quadráticas muitas vezes pára. Chegamos a esse objeto amado de todos os jornalistas quando eles entrevistam matemáticos – uma fórmula. Perguntas intermináveis podem ser feitas que envolvem colocar valores de 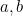 e
e  na fórmula para dar (duas) respostas. Mas a matemática não é de todo isto. Encontrar uma fórmula é apenas o primeiro passo de um longo caminho. Temos que perguntar, o que significa a fórmula; o que ela nos diz sobre o universo; será que ter uma fórmula realmente importa? Vamos agora ver para onde essa fórmula nos levará.
na fórmula para dar (duas) respostas. Mas a matemática não é de todo isto. Encontrar uma fórmula é apenas o primeiro passo de um longo caminho. Temos que perguntar, o que significa a fórmula; o que ela nos diz sobre o universo; será que ter uma fórmula realmente importa? Vamos agora ver para onde essa fórmula nos levará.
Uma surpresa para os gregos, um pouco de origami matemático e um senso de proporção
Agora, vamos rapidamente avançar 1000 anos para os Antigos Gregos e ver o que eles fizeram com as equações quadráticas. Os gregos eram magníficos matemáticos e descobriram grande parte da matemática que ainda hoje usamos. Uma das equações que eles estavam interessados em resolver era a (simples) equação quadrática
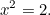 |

Eles sabiam que esta equação tinha uma solução. Na verdade é o comprimento da hipotenusa de um triângulo angulado à direita que tinha lados de comprimento um.
Segue-se do teorema de Pitágoras que, se um triângulotriângulo angular tem lados mais curtos  e
e  e hipotenusa
e hipotenusa  depois
depois
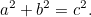 |
Colocando 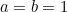 e
e  depois
depois 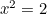 . Assim
. Assim 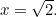
Então, o que é  neste caso? Ou, para fazer a pergunta que os gregos fizeram, que tipo de número é? A razão pela qual isto importava era o sentido de proporção do grego. Eles acreditavam que todos os números estavam em proporção uns com os outros. Para ser preciso, isto significava que todos os números eram frações da forma
neste caso? Ou, para fazer a pergunta que os gregos fizeram, que tipo de número é? A razão pela qual isto importava era o sentido de proporção do grego. Eles acreditavam que todos os números estavam em proporção uns com os outros. Para ser preciso, isto significava que todos os números eram frações da forma 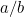 onde
onde  e
e  são números inteiros. Números como 1/2, 3/4 e 355/113 são todos exemplos de frações. Era natural esperar que
são números inteiros. Números como 1/2, 3/4 e 355/113 são todos exemplos de frações. Era natural esperar que  fosse também uma fração. A grande surpresa foi que não é. Na verdade
fosse também uma fração. A grande surpresa foi que não é. Na verdade
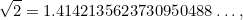 |
onde os pontos  significam que a expansão decimal de
significam que a expansão decimal de  continua até ao infinito sem qualquer padrão discernível. (Encontraremos esta situação novamente mais tarde quando soubermos do caos.)
continua até ao infinito sem qualquer padrão discernível. (Encontraremos esta situação novamente mais tarde quando soubermos do caos.)
 foi o primeiro número irracional (ou seja, um número que não é uma fração, ou racional), a ser reconhecido como tal. Outros exemplos incluem
foi o primeiro número irracional (ou seja, um número que não é uma fração, ou racional), a ser reconhecido como tal. Outros exemplos incluem 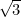 ,
,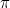 ,
,  e na verdade “a maioria” dos números. Levou até o século XIX para que tivéssemos uma boa maneira de pensar sobre esses números. A descoberta de que
e na verdade “a maioria” dos números. Levou até o século XIX para que tivéssemos uma boa maneira de pensar sobre esses números. A descoberta de que  não era um número racional causou tanto grande excitação (100 bois foram sacrificados como resultado) como grande choque, com o descobridor tendo que cometer suicídio. (Que isto seja um terrível aviso para os matematicamente perspicazes!) Neste ponto os gregos desistiram da álgebra e voltaram-se para a geometria.
não era um número racional causou tanto grande excitação (100 bois foram sacrificados como resultado) como grande choque, com o descobridor tendo que cometer suicídio. (Que isto seja um terrível aviso para os matematicamente perspicazes!) Neste ponto os gregos desistiram da álgebra e voltaram-se para a geometria.
Far de ser um número obscuro, nos encontramos  regularmente: sempre que usamos um pedaço de papel A4. Na Europa, os tamanhos de papel são medidos em tamanhos A, sendo o A0 o maior com uma área de
regularmente: sempre que usamos um pedaço de papel A4. Na Europa, os tamanhos de papel são medidos em tamanhos A, sendo o A0 o maior com uma área de 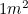 . Os tamanhos A têm uma relação especial entre eles. Se fizermos agora um pouco de origami, pegando numa folha de papel A1 e depois dobrando-a ao meio (ao longo do seu lado mais comprido), obtemos papel A2. Dobrá-lo ao meio dá novamente A3, e novamente dá A4, etc. No entanto, o papel é concebido para que as proporções de cada um dos tamanhos A sejam as mesmas – ou seja, cada pedaço de papel tem a mesma forma.
. Os tamanhos A têm uma relação especial entre eles. Se fizermos agora um pouco de origami, pegando numa folha de papel A1 e depois dobrando-a ao meio (ao longo do seu lado mais comprido), obtemos papel A2. Dobrá-lo ao meio dá novamente A3, e novamente dá A4, etc. No entanto, o papel é concebido para que as proporções de cada um dos tamanhos A sejam as mesmas – ou seja, cada pedaço de papel tem a mesma forma.
Podemos colocar a questão da proporção que isto é. Comece com um pedaço de papel com lados x e y com x o lado mais comprido. Agora divida isto em dois para dar outro pedaço de papel com os lados y e x/2 sendo agora y o lado mais comprido. Isto é ilustrado à direita.
As proporções do primeiro pedaço de papel são 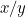 e as do segundo são
e as do segundo são 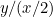 ou
ou 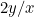 . Nós queremos que estas duas proporções sejam iguais. Isto significa que
. Nós queremos que estas duas proporções sejam iguais. Isto significa que
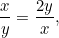 |
ou
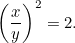 |
Outra equação quadrática! Felizmente, é uma que já conhecemos. Resolvendo-a descobrimos que
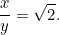 |
Este resultado é fácil de verificar. Basta pegar uma folha de papel A4 (ou A3 ou A5) e medir os lados. Também podemos calcular o tamanho de cada folha. A área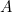 de um pedaço de papel A0 é dada por
de um pedaço de papel A0 é dada por
>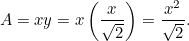
|
Mas nós sabemos que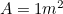 por isso temos outra equação quadrática para o lado mais comprido
por isso temos outra equação quadrática para o lado mais comprido de A0, dado por
de A0, dado por
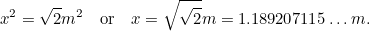 |
Isto significa que o lado mais longo de A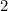 é dado por
é dado por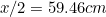 (porquê?) e o de A
(porquê?) e o de A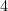 por
por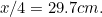 . Verifique estas em suas próprias folhas de papel.
. Verifique estas em suas próprias folhas de papel.
O papel usado nos Estados Unidos, chamado foolscap, tem uma proporção diferente. Para ver o porquê, voltamos aos gregos e a outra equação quadrática. Tendo causado tal sofrimento, a equação quadrática se redime na busca das proporções perfeitas: uma busca que continua até hoje no desenho de conjuntos de filmes, e pode ser vista em muitos aspectos da natureza.
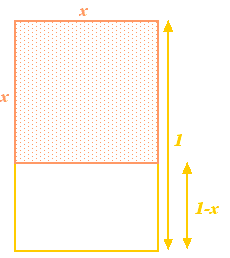
Comecemos com um retângulo, e depois removamos um quadrado com o mesmo comprimento lateral que o lado mais curto do retângulo. Se o lado mais longo do retângulo tem comprimento 1 e o lado mais curto tem comprimento  , então o quadrado tem lados de comprimento
, então o quadrado tem lados de comprimento  . Removê-lo do retângulo dá um retângulo menor com o lado mais longo
. Removê-lo do retângulo dá um retângulo menor com o lado mais longo  e o lado menor
e o lado menor 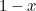 . Até agora, tão abstrato. No entanto, os gregos acreditavam que o retângulo que tinha as proporções mais estéticas (o chamado Retângulo Dourado) era aquele para o qual os retângulos grandes e pequenos construídos acima têm as mesmas proporções. Para que isto seja possível devemos ter
. Até agora, tão abstrato. No entanto, os gregos acreditavam que o retângulo que tinha as proporções mais estéticas (o chamado Retângulo Dourado) era aquele para o qual os retângulos grandes e pequenos construídos acima têm as mesmas proporções. Para que isto seja possível devemos ter
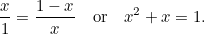 |
Esta é mais uma equação quadrática: uma muito importante que surge em todo o tipo de aplicações. Ela tem a solução (positiva)
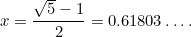 |
O número  é chamado de proporção áurea e é frequentemente denotado pela letra grega
é chamado de proporção áurea e é frequentemente denotado pela letra grega 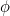 .
.

O Rectângulo Dourado pode ser visto na forma de janelas, especialmente em casas georgianas. Mais recentemente, o Rectângulo Dourado também pode ser encontrado como a “forma perfeita” para fotografias e imagens de filmes. A equação quadrática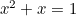 também surge em estudos das populações de coelhos e no padrão em que as sementes de girassóis e as folhas nos caules das plantas são dispostas. Todas estas estão ligadas com a proporção de Ouro através da sequência de Fibonacci que é dada por
também surge em estudos das populações de coelhos e no padrão em que as sementes de girassóis e as folhas nos caules das plantas são dispostas. Todas estas estão ligadas com a proporção de Ouro através da sequência de Fibonacci que é dada por
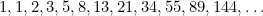 |

Sementes de girassol, ordenados usando números de Fibonacci |
O Partenon, incorporando a Razão de Ouro |
Nesta sequência cada termo é a soma dos dois termos anteriores. Fibonacci descobriu-o no século XV, numa tentativa de prever a população futura de coelhos. Se você pegar a razão de cada termo para o que se segue, você obtém a seqüência de números
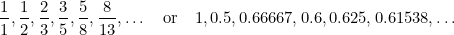 |
e estes números se aproximam cada vez mais (você adivinhou) da Razão de Ouro 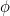 .
.
Encontrando ambas as raízes da equação quadrática acima podemos realmente encontrar uma fórmula para o n-ésimo termo na sequência de Fibonacci. Se  é o número
é o número 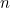 com
com 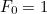 e
e 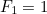 então
então  é dado pela fórmula
é dado pela fórmula
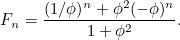 |
Cónicos ligam equações quadráticas às estrelas
Os gregos também estavam muito interessados na forma dos cones. A figura à esquerda mostra um cone típico.
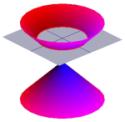
Metade do cone pode ser visualizada como a propagação da luz vinda de uma tocha. Agora, se brilhar uma tocha sobre uma superfície plana, como uma parede, então você verá várias formas ao mover a tocha ao redor. Estas formas são chamadas seções cônicas e são as curvas que você obtém se você pegar uma fatia através de um cone em vários ângulos diferentes. Precisamente estas curvas foram estudadas pelos gregos, que reconheceram que existiam basicamente quatro tipos de secção cónica. Se você pegar uma seção horizontal através do cone, então você recebe um círculo. Uma secção num pequeno ângulo em relação à horizontal dá-lhe uma elipse. Se você pegar uma seção vertical então você recebe uma hipérbole e se você pegar uma seção paralela a um lado do cone então você recebe uma parábola. Estas curvas são ilustradas abaixo.
 |
 |
 |
 |
 |
 |
 |
 |
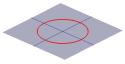
 Uma cruz…seção de um cone pode ser um círculo …. Uma cruz…seção de um cone pode ser um círculo …. |
 … uma elipse … … uma elipse … |
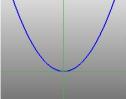 … uma parábola … … uma parábola … |
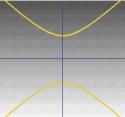
….ou uma hiperbola. |
Seções cónicas entram na nossa história porque cada uma delas é descrita por uma equação quadrática. Em particular, se 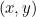 representa um ponto em cada curva, então uma equação quadrática liga
representa um ponto em cada curva, então uma equação quadrática liga  e
e 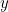 . Nós temos:
. Nós temos:
O círculo: 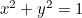 ;
;
A elipse: 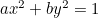 ;
;
A hipérbole: 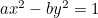 ;
;
>
A parábola: 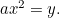
Estas curvas eram conhecidas e estudadas desde os gregos, mas tirando o círculo, não pareciam ter qualquer aplicação prática. No entanto, como veremos na próxima edição de Plus, uma ligação entre as equações quadráticas e as cónicas, aliada a um poderoso acaso da sorte, levou a uma compreensão da forma como o universo funcionava, e no século XVI chegou o momento das cónicas mudarem o mundo.
Sobre os autores
Chris Budd é Professor de Matemática Aplicada no Departamento de Ciências Matemáticas da Universidade de Bath, e Cadeira de Matemática na Instituição Real em Londres.
Chris Sangwin é membro da equipe da Escola de Matemática e Estatística da Universidade de Birmingham. Ele é Pesquisador no Centro de Rede de Apoio à Aprendizagem e Ensino de Matemática, Estatística e Pesquisa Operacional.
>
Antes de escrever o popular livro de matemática Mathematics Galore!, publicado pela Oxford University Press.
>
Este artigo foi inspirado em parte por um notável debate na Câmara dos Comuns Britânica sobre o tema das equações quadráticas. O registo deste debate pode ser encontrado em Hansard, Câmara dos Comuns do Reino Unido, 26 de Junho de 2003, Colunas 1259-1269, 2003, que está disponível online no website da Câmara dos Comuns Hansard Debate.