Een belangrijke vraag is, hoe zijn priemgetallen verdeeld over de gehele getallen? Het antwoord is, in een paar woorden, tamelijk willekeurig, gegeven bepaalde basisstatistieken…
 Bill Casselman
Bill Casselman
Universiteit van British Columbia, Vancouver, Canada
Email Bill Casselman
| |
|
Inleiding
Vele jaren geleden vermoedde men dat er een oneindig aantal paren priemgetallen $p$, $q$ met $q = p+2$ bestaan. Er is enige recente (en beroemde) vooruitgang geboekt met dit probleem. Ik zal weinig zeggen over de recente vooruitgang, maar in plaats daarvan bespreken wat we verwachten – eerder dan wat we weten – over dergelijke paren. Niets van wat ik zal zeggen is nieuw, en ik heb tot op zekere hoogte slechts uitgewerkt wat Andrew Granville zegt in zijn recente uiteenzetting over de recente vorderingen.
Hoeveel priemgetallen verwachten we?
Een priemgetal is een positief geheel getal dat geen delers heeft behalve zichzelf en $1$. De definitie is eenvoudig, maar zodra men de betekenis van priemgetallen begint te onderzoeken, realiseert men zich dat zij veel subtieler gedrag vertonen. Een belangrijke vraag is, hoe zijn de priemgetallen verdeeld over de gehele getallen? Het antwoord is, in een paar woorden, tamelijk willekeurig, gegeven bepaalde basisstatistieken. Wat bedoel ik daarmee?
Wel, hier is een vierkante matrix met alle priemgetallen tot $400$:

Er zijn enkele patronen in deze matrix, waarvan ik er later enkele zal bespreken. De meeste die u waarneemt, worden veroorzaakt door een artefact van het scherm. Bijvoorbeeld, elke andere kolom is in wezen leeg, en dit komt omdat het enige even priemgetal $2$ is. Ook elke vijfde kolom is in essentie leeg. Interessanter zijn de tweelingpriemparen (waarvan sommige niet zo goed zichtbaar zijn omdat ze over twee rijen verdeeld zijn, zoals $59$, $61$), en ook enkele patronen die verband houden met de laatste cijfers die worden weergegeven. Dit zijn wat men zou kunnen noemen lokale patronen. Er zijn geen globale patronen zichtbaar.
Er is veel moeite gestoken in uiterst efficiënte manieren om priemgetallen te produceren, maar tegenwoordig kost het zelfs een zeer eenvoudig programma slechts een kleine hoeveelheid tijd om grote lijsten van priemgetallen te maken. Een van de meest vruchtbare programma’s maakt een grote lijst van priemgetallen en berekent dan met behulp daarvan de functie $140pi(n)$, het aantal priemgetallen $140 n$.
Een van de dingen waarvoor dit gebruikt kan worden is om een ruw idee te krijgen van de frequentie van priemgetallen. Er zijn $135$ priemgetallen in het bereik $$:
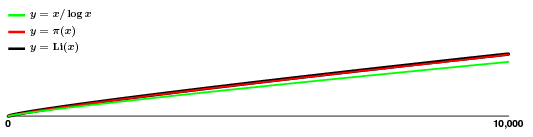
De benadering ziet er goed uit! Dus ook al stuitert $pi(x)$ een beetje rond, ogenschijnlijk zonder veel patroon, we hebben er een vrij goede schatting voor, wat betekent dat we een goed idee hebben van hoe de priemgetallen groeien, althans gemiddeld.
Het moet echter niet vergeten worden dat de ogenschijnlijke gladheid bedrieglijk is. Van dichtbij ziet u hoe de bovenste twee curven eruit zien:

Commentaar?
Heuristische redenering over tweelingpriemgetallen
Tweelingpriemgetallen zijn een paar $p$, $p+2$ die beide priemgetallen zijn. In een van de bovenstaande grafieken zien we bijvoorbeeld de tweelingpriemgetallen $$ , , , , $$
en andere. Men vermoedt dat het er oneindig veel zijn, maar hoewel er veel empirisch bewijs voor is, is het nog niet bewezen.
Het sterkste bewijs is misschien wel een formule die het aantal $\pi_{2}(x)$ van tweelingpriemgetallen $\le x$ opmerkelijk goed benadert. Ik ben niet helemaal zeker van de oorsprong van deze formule, maar ze verscheen voor het eerst in een artikel van G. H. Hardy en J. E. Littlewood (zelf een tweelingpriempaar) uit 1923. Het artikel bevat verschillende gelijksoortige formules, alle gebaseerd op dezelfde methode, die zij al eerder hadden gebruikt om vele problemen aan te pakken. Dit was hun cirkelmethode. Hun afleiding van de formule voor $pi_{2}(x)$ is helemaal niet rigoureus, maar wel zeer overtuigend. Er is een beknopt verslag van in een bijlage bij het artikel van Andrew Granville.
Maar vlak na de Tweede Wereldoorlog stelde Lord Cherwell (Frederick Lindemann) een meer elementaire probabilistische (en nog steeds niet rigoureuze) afleiding voor. Dit leidde tot een samenwerking met E.M. Wright en uiteindelijk tot een postume gezamenlijke publicatie. Dit wordt uitgelegd in paragraaf 22.20 van de bekende tekst van Hardy en Wright. Een iets meer elementaire versie hiervan is ook te vinden in een appendix van Granville’s artikel (Section 2.5). Ik volg hem.
Het uitgangspunt voor de plausibele redenering is onze schatting voor $\pi(x)$, het aantal priemgetallen kleiner dan of gelijk aan $x$. Het basisidee van de afleiding is dat de priemgetallen voor een groot deel willekeurig verdeeld zijn. We weten dat in de buurt van $x$ de dichtheid van priemgetallen ongeveer $1/log x$ is. Als de priemgetallen willekeurig verdeeld zouden zijn, dan zou de kans dat twee willekeurige getallen in de buurt van $x$ priemgetallen zijn gewoon het product van de lokale kansen zijn, wat $1/\log^{2} x$ is. Dit is zeker een misleidende redenering, want als $n > 2$ is de kans dat zowel $n$ als $n+1$ priemgetallen zijn $0$, terwijl het feit dat $p$ een priemgetal is de kans dat $p+2$ een priemgetal is lijkt te vergroten. Soortgelijke overwegingen zijn er ook in verband met mogelijke deelbaarheid door andere kleine priemgetallen in de buurt van $x$.
Er is een eenvoudig feit in dit verhaal. Als $q$ een willekeurig priemgetal is, dan is de kans om een geheel getal te kiezen dat niet deelbaar is door $q$ $1-1/q$. De kans om er twee te kiezen die niet deelbaar zijn door $q$ is dus het product $(1 – 1/q)^{2}$. Stel dat $p$ en $p+2$ beide priemgetallen zijn, dan is noch $p$ noch $p+2$ deelbaar door $q$. Als $q = 2$, gebeurt dit $1/2$ per keer. Als $q = 2$, is de kans dat $p 0$ en $p -2$ modulo $q$ is $(1 – 2/q)$. Vanwege de Chinese Remainder Theorema is deelbaarheid door twee priemgetallen een onafhankelijke gebeurtenis. Dus als $x$ groot is en $Q$ relatief klein, dan is de kans dat een paar getallen $m$ en $n$ in de buurt van $x$ geen veelvoud zijn van een priem tot $Q$ $ { 1}over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} } \. $$
Laat $\Gamma_{Q}$ de verhouding zijn van dit tot $\prod_{q \le Q}(1 – 2/q)$: $$ \Gamma_{Q} = { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \over (1 – 2/q) } $$ We hebben $$ { 1 – 2/q ^{2} ^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \over (1 – 1/q)^{2} } = {(1 – 1/q)^{2} } = 1 – { 1 \over (q -1)^{2} } \$$ Een standaard criterium stelt dat dit product convergeert als de som $ 1/(q-1)^{2}$ convergeert. Maar het convergeert, want de integraaltoets zegt ons dat $\sum 1/n^{2}$ convergeert. Dit product convergeert dus eigenlijk naar een getal $\Pi_{\infty}$ als $Q rechtarrow \infty$. Laat $C_{2}$ de inverse zijn. In paragraaf 2.5 van Granville’s artikel staat dat het op dit punt intuïtief redelijk zou moeten zijn dat het aantal $\pi_{2}(x)$ van tweelingpriemgetallen $\le x$ benaderd wordt door $$ \Pi_{2}(x) = C_{2} \{int_{2}^{\infty} { dx x over \log^{2} x } \$$
In de tekst van Hardy en Wright staat een zorgvuldiger analyse die de intuïtieve sprong wat duidelijker maakt.
De waarde van de constante hier werd lang geleden door J. W. Wrench berekend op ongeveer $1.32032363169373914785562422002911155686525 $. Hier volgt een vergelijking van enkele waarden van $pi_{2}(x)$ en de formule in de reeks $$: $$ \matrix{ n & 10.000 & 20.000 & 30.000 & 40.000 & 50.000 \cr \pi_{2}(n) & 205phantom{.0} & 342 fantoom{.0} & 467 fantoom{.0} & 591 \phantom{.0} & 705 fantoom & \cr \Pi_{2}(x) & 214,2 & 357,7 & 486,7 & 607,4 & 722,5 \cr } $$ $$ \matrix{ n & 60.000 & 70.000 & 80.000 & 90.000 & 100.000 \cr \pi_{2}(n) & 811 \phantom{.0} & 905 \phantom{.0} & 1007 fantoom{.0} & 1116 \phantom{.0} & 1224 & 833.3 & 940.9 & 1045.7 & 1148.2 & 1248.7 \cr } $$
Commentaren?
Dickson’s conjecture
Tweelingpriemgetallen zijn een speciaal geval van iets veel algemeners. Men kan zich afvragen of er oneindig veel paren $p$, $p+4$ of $p$, $p+6$ zijn die priemgetallen zijn. Of $p$, $p+10$? Het geval van $p$ en $p+10$ wordt zeker gesuggereerd door een van de afbeeldingen hierboven, waarin zulke paren gemakkelijk zichtbaar zijn. Hoe zit het met een soort drieparen? Stel dat $a_{1}$, $a_{2}$, $a_{k}$ , $a_{k}$ een matrix van gehele getallen vormen. Kunnen we dan verwachten dat er een oneindig aantal verzamelingen $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$ zijn die allemaal priem zijn?
Men moet een beetje voorzichtig zijn. Er zijn geen priemparen van de vorm $p$, $p+1$ (voorbij $p = 2$), want een van deze twee getallen moet deelbaar zijn door $2$. Evenzo zijn er voorbij $p = 3$ geen priemdriehoeken $p$, $p+2$, $p+4$ omdat één van deze getallen deelbaar moet zijn door $3$.
Dit laatste voorbeeld moet verhelderend zijn. Het getal $p+4$ is deelbaar door $3$ als en slechts als $p+1$ deelbaar is door $3$. Dus $3$ deelt een van de getallen $p$, $p+2$, $p+4$ als en slechts als het deelt $p$, $p+1$, $p+2$. Maar dit zal zeker gebeuren, want het laatste drietal omvat duidelijk alle getallen modulo $3$.
In het algemeen zegt men dat $p$ een obstructie is voor de matrix $(a_{i})$ als $p$ altijd minstens één deelt van elke rij $n+a_{i}$ ($i = 1$, $k$, $k$). Dit gebeurt alleen en alleen als de getallen $a_{i} \{{i}; {{i} mod} \p$ geheel $Z/p$ vullen.
Dit kan nooit gebeuren als $p > k$, dus om na te gaan of een of andere $p$ $(a_{i})$ belemmert hoeven we alleen maar na te gaan of de $a_{i}$ $Z/p$ voor alle $p \le k$ beslaan. We noemen de rij $(a_{i})$ ontvankelijk als ze geen priemobstakels heeft.
Zo is bijvoorbeeld $(1,3,7,9)$ een ontvankelijke rij, omdat, zoals eenvoudig te controleren is, noch $2$ noch $3$ een obstructie is. Verschillende priemreeksen die in dit patroon passen, zijn te zien in een van de diagrammen hierboven. Andere voorbeelden zijn (a) $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
Er bestaan willekeurig grote toelaatbare verzamelingen. In feite:
Stelling. Als $a_{1}$ tot $a_{k}$ een willekeurige verzameling verschillende priemgetallen $> k$ is, vormen ze een toelaatbare verzameling.
Waarom is dit? Als $p$ een willekeurig priemgetal is waarbij $p> k$, dan hebben we al gezien dat het geen obstructie kan zijn. Maar als $p kleiner is dan k$, dan kan hij geen van de $a_{i}$ delen, die geen van alle congruent kunnen zijn met $0$ modulo $p$. De $a_{i}$ vullen dus $Z/p$ niet op.
Een speciaal geval van een vermoeden van L. E. Dickson is dat als er geen priemobstakels zijn voor $(a_{i})$, er oneindig veel priemreeksen bestaan van de vorm $(n +a_{i})$.
Wat is er de laatste tijd gebeurd
Dit is niet de plaats om het hele verhaal te vertellen, dat is op andere plaatsen al grondig behandeld. Ik raad vooral het Quanta artikel van Erica Klarreich aan voor een populair verslag, en Granville’s essay voor een meer technisch verslag. Ik wil alleen wat preciezer dan in Klarreichs verslag aangeven wat de beroemdste van de nieuwe resultaten is.
Het is te danken aan Yitang Zhang. De eenvoudigste verklaring van wat hij bewees is dat er een oneindig aantal intervallen $[n, n+70.000.000)$ bestaan die ten minste twee priemgetallen bevatten. Dit is zwakker dan het tweelingpriem-vermoeden, maar komt er conceptueel zeer dicht bij in de buurt. In later werk (door veel wiskundigen) is de grootte van de kloof sterk verkleind, maar er is vermoedelijk geen manier om hem met de huidige methoden tot $2$ te verkleinen.
Zoals Granville uitlegt, is Zhangs eerste en aantoonbaar zijn belangrijkste resultaat dat er $k$ bestaat met de eigenschap dat als $a_{1}$, $\ldots$ , $a_{k}$ een toelaatbare verzameling van $k$ elementen is, er een oneindig aantal $n$ bestaat zodanig dat ${ n +a_{i} \{i}$ minstens twee priemgetallen bevat. (In Klarreichs Quanta artikel wordt de rij een “kam” genoemd. Bedenk dat we volgens Dickson’s conjectuur zouden moeten kunnen zeggen dat alle $k$ priemgetallen zijn). Zhang bewees zelfs dat deze bewering waar is voor een bepaalde $k =3.500.000$ over een interval van $70.000.000$. De inmiddels beroemde consequentie is dat er voor een bepaalde $m =70.000.000$ oneindig veel priemparen $p$, $p+m$ bestaan.
Lees verder
- Lord Cherwell en E. M. Wright, “The frequency of prime patterns”, The Quarterly Journal of Mathematics 11 (1960).
Degenen die iets weten van het leven van Lord Cherwell, ook bekend als Frederick Lindemann, zullen zeer verrast zijn te vernemen over zijn bijdrage aan de getaltheorie. De Wikipedia-biografie geeft niet voldoende de redenen aan voor zijn slechte reputatie als belangrijkste wetenschappelijk adviseur van Churchill tijdens de Tweede Wereldoorlog.
- L. E. Dickson, “A new extension of Dirichlet’s theorem on prime numbers”, Messenger of Mathematics 33.
Zie ook de Wikipedia entry over Dickson’s conjecture.
- Andrew Granville, “Priemgetallen in intervallen van begrensde lengte”. Beschikbaar via zijn home page.
- G. H. Hardy, Ramanujan, Cambridge University Press.
Sectie 2.5 bevat een ideale afleiding van een mogelijke formule voor $pi(x)$.
- G. H. Hardy en J. E. Littlewood, “Some problems of ‘Partitio numerorum’ III: on the expression of a number as a sum of primes”, Acta Mathematica 44 (1923).
- G. H. Hardy and E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, “Together and alone, closing the prime gap”, Quanta November 19, 2013.
- B. Riemann, “Over het aantal priemgetallen kleiner dan een gegeven hoeveelheid”. Een Engelse vertaling van deze klassieker door David Wilkins is beschikbaar via een link in Wikipedia.
Hierin wordt o.a. een afleiding geschetst van de benaderingsformule voor $pi(x)$.
- J. W. Wrench, “Evaluation of Artin’s constant and the twin-prime constant”, Mathematics of Computation 76 (1961).
Een vroege berekening van $C_{2}$.
- Lijsten van priemgetallen tot $1.000.000.000.000$
- Een lijst van de eerste 20.000 tweelingpriemgetallen.
 Bill Casselman
Bill Casselman
Universiteit van Brits Columbia, Vancouver, Canada
Email Bill Casselman