De hoek die gemaakt wordt als de straal
om de cirkel wordt gewikkeld:
 |
1 Radiaal is ongeveer 57,2958 graden. |
Waarom “57,2958…” graden? Dat zien we zo.
De radiaal is een zuivere maat op basis van de straal van de cirkel:
Radiaal: de hoek die gemaakt wordt als we de straal
nemen en die om de cirkel wikkelen.
Radialen en Graden
Laten we eens kijken waarom 1 radiaal gelijk is aan 57.2958… graden:
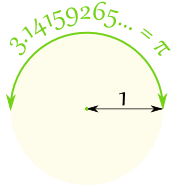
In een halve cirkel zittenπ radialen, dat is ook 180°
Om van radialen naar graden te gaan: vermenigvuldigen met 180, delen door π
Om van graden naar radialen te gaan: vermenigvuldigen met π, delen door 180
Hier volgt een tabel met equivalente waarden:
| Graden | Radialen (exact) |
Radialen (bij benadering) |
|---|---|---|
| 30° | π/6 | 0.524 |
| 45° | π/4 | 0.785 |
| 60° | π/3 | 1.047 |
| 90° | π/2 | 1.571 |
| 180° | π | 3.142 |
| 270° | 3π/2 | 4.712 |
| 360° | 2π | 6.283 |
Exemplaar: Hoeveel radialen in een volledige cirkel?
Stel je voor dat je stukjes touw afknipt precies de lengte van het middelpunt tot de omtrek van een cirkel …
… hoeveel stukjes heb je nodig om eenmaal de cirkel rond te gaan?
Antwoord: 2π (of ongeveer 6,283 stukjes touw).
Radialen geprefereerd door wiskundigen
Omdat de radiaal gebaseerd is op het zuivere idee van “de straal die langs de omtrek wordt gelegd”, geeft hij vaak eenvoudige en natuurlijke resultaten wanneer hij in de wiskunde wordt gebruikt.
Kijk bijvoorbeeld eens naar de sinusfunctie voor zeer kleine waarden:

