Vierdejaars Alice vraagt, “Hoeveel diagonalen zitten er in een decagon?”
Goede vraag, Alice. Maar in plaats van je een antwoord te geven, laat ik je zien hoe je het zelf kunt uitrekenen. En dat niet alleen, ik zal je laten zien hoe je het antwoord kunt vinden voor elke veelhoek, zelfs als die 20, of 50, of 2000 zijden heeft!
Klaar? Laten we beginnen met een eenvoudig voorbeeld. We gaan uit van een veelhoek met 8 zijden (dat heet een achthoek), zoals dit:
Nu, deze veelhoek, omdat hij acht zijden heeft, heeft ook acht hoekpunten. Het lijkt een beetje overweldigend om alle diagonalen uit te zoeken, dus laten we ons concentreren op één hoekpunt. Hoeveel diagonalen kun je tekenen in een achthoek, die allemaal bij één hoekpunt beginnen?
Het antwoord op die vraag is vijf. Kijk eens naar onderstaand diagram:

In dit diagram heb ik de diagonaal links net onder het bovenste hoekpunt gekozen, en ik heb diagonalen getekend naar elk hoekpunt waar ik een diagonaal naar toe kan trekken. Naar welke diagonalen kan ik niet diagonaal tekenen? Wel, ik kan geen diagonaal trekken van een hoekpunt terug naar zichzelf, en ik kan geen diagonalen trekken naar de twee hoekpunten naast dat hoekpunt (want dat zouden geen diagonalen zijn; dat zouden zijden zijn!).
Dus er zijn drie hoekpunten waar ik geen diagonalen naar toe kan trekken vanaf dat hoekpunt. Acht hoekpunten in totaal, min de drie die ik niet kan tekenen, blijven er vijf over. Dat is belangrijk om te onthouden: trek 3 af van het aantal hoekpunten, en je hebt het aantal diagonalen dat je vanuit elk hoekpunt kunt trekken.
Maar dat is maar één hoekpunt! Je kunt toch diagonalen tekenen vanuit elk hoekpunt? Tuurlijk! En er zijn acht hoekpunten in onze achthoek, dus we nemen het aantal diagonalen per hoekpunt, en vermenigvuldigen dat met het aantal hoekpunten: 5 x 8 = 40.
Je zou geneigd kunnen zijn te denken dat dat ons antwoord is, maar dat is het niet. Waarom niet? Omdat we elke diagonaal twee keer hebben geteld! Elke diagonaal heeft twee hoekpunten, dus we hebben hem geteld vanaf het ene uiteinde, en we hebben hem ook geteld vanaf het andere uiteinde. Dus om het werkelijke aantal diagonalen te krijgen, moeten we ons antwoord delen door 2. 40 / 2 = 20. Er zijn twintig diagonalen in een achthoek.
Laten we die redenering eens proberen op een veelhoek met 2000 zijden. Ik ga geen 2000-gon voor je tekenen; we moeten gewoon de redenering uitwerken zonder plaatje.
- Kies een hoekpunt. Hoeveel diagonalen kun je vanuit dat hoekpunt trekken? Antwoord: 2000 – 3 = 1997.
- Hoeveel hoekpunten in totaal? Antwoord: 2000
- Hoeveel diagonalen geteld vanuit alle hoekpunten? Antwoord: 1997 x 2000 = 3.994.000
- Oeps! We hebben elke diagonaal twee keer geteld! Hoe komen we van de dubbelen af? Antwoord: 3994000 / 2 = 1.997.000
Dus een 2000-gon heeft 1.997.000 diagonalen!
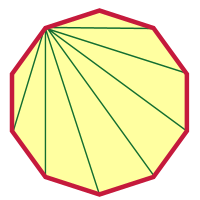
Na zoiets geks als een 2000-gon te hebben gedaan, moet een decagon niet zo moeilijk meer lijken, toch? Ik zal je op weg helpen, en jij kunt het vanaf hier afmaken. Ik koos een hoekpunt en tekende diagonalen vanuit dat hoekpunt.
Hoeveel zijn het er? Kon je uitvinden hoeveel het er waren zonder naar het plaatje te kijken?
Kun je het vanaf hier uitrekenen? Ik hoop van wel. Veel succes, Alice.
Tussen haakjes, er is een formule die je kunt gebruiken; die ziet er zo uit: D = n(n – 3)/2. Maar eerlijk gezegd verwacht ik niet dat mijn leerlingen die uit hun hoofd leren. Ik verwacht dat ze onthouden hoe we het hier beredeneren. Als je de logica begrijpt, is het zelfs beter dan een formule te hebben!