Math Modeling

by admin Leave Comment

Leerdoelen

  • Inleiding tot stukgewijze functies
    • Definieer stukgewijze functie
    • Evalueer een piecewise functie
    • Schrijf een piecewise functie gegeven een toepassing
  • Graf Piecewise Functions
    • Gegeven een piecewise-gedefinieerde functie, een grafiek schetsen
    • Het domein en bereik van een stukgewijze functie beschrijven, gegeven een grafiek

Sommige functies komen in stukken. In dit gedeelte zullen we leren hoe we functies kunnen definiëren en grafieken die in wezen verzamelingen van discrete stukken zijn. Voorbeelden van iets dat op deze manier gedefinieerd is, zijn het ontwerpen van het profiel van een auto, het berekenen van uw mobiele telefoon abonnement, en het berekenen van inkomstenbelastingtarieven. Uw belastingtarief hangt bijvoorbeeld af van uw inkomen en is hetzelfde voor een reeks inkomens, zoals blijkt uit de onderstaande tabel:

Marginal Tax Rate Single Taxable Income Married Filing Jointly or Qualified Widow(er) Taxable Inkomen Gezamenlijkwonend of in aanmerking komende weduwe(n) belastbaar inkomen Belastbaar inkomen gezinshoofd
10% $0 – $9.000 $0 – $9.000 $0 – $9.000 Belastingtarief275 $0 – $18,550 $0 – $9,275 $0 – $13,250
15% $9,276 – $37,650 $18,551 – $75,300 $9,276 – $37,650 $13,251 – $50,400
25% $37,651 – $91,150 $75,301 – $151,900 $37,651 – $75,950 $50,401 – $130,150
28% $91,151 – $190,150 $151,901 – $231,450 $75,951 – $115,725 $130,151 – $210,800
33% $190,151 – $413,350 $231,451 – $413,350 $115,726 – $206,675 $210,801 – $413,350
35% $413,351 – $415,050 $413,351 – $466,950 $206,676 – $233,475 $413,351 – $441,000
39.6% $415.051+ $466.951+ $233.476+ $441.001+

Een stukgewijze functie is een functie waarin meer dan één formule wordt gebruikt om de uitvoer over verschillende stukken van het domein te definiëren.

Wij gebruiken stukgewijze functies om situaties te beschrijven waarin een regel of relatie verandert naarmate de invoerwaarde bepaalde “grenzen” overschrijdt. Zo komen we in het bedrijfsleven vaak situaties tegen waarin de kosten per stuk van een bepaald artikel worden verdisconteerd zodra het bestelde aantal een bepaalde waarde overschrijdt. Belastingtarieven zijn een ander voorbeeld van stapsgewijze functies. Neem bijvoorbeeld een eenvoudig belastingstelsel waarin inkomens tot $10.000 belast worden tegen 10%, en alle bijkomende inkomens tegen 20%. De belasting op een totaal inkomen, S, zou 0,1S zijn als S meer dan $10.000 bedraagt en 1000 + 0,2 (S – $10.000), als S> $10.000.

stuksgewijze functie

Een stuksgewijze functie is een functie waarin meer dan één formule wordt gebruikt om de uitvoer te definiëren. Elke formule heeft zijn eigen domein, en het domein van de functie is de unie van al deze kleinere domeinen. We noteren dit idee als volgt:

f-links(x-rechts)=begin{gevallen}:formule 1 als x in domein 1 zit}:formule 2 als x in domein 2 zit}:formule 3 als x in domein 3 zit}:eind{gevallen}

In de stukgewijze notatie is de absolute-waardefunctie

|x|=

x|=<0

Evalueer een stukgewijs gedefinieerde functie

In het eerste voorbeeld zullen we laten zien hoe we een stukgewijs gedefinieerde functie kunnen evalueren. Merk op hoe belangrijk het is om op het domein te letten om te bepalen welke uitdrukking gebruikt moet worden om de invoer te evalueren.

Voorbeeld

Gegeven aan de functie

f(x)=xxx+3{ begin{gevallen}7x+3{ als }x<0x+6{ als }xx+0}x-eind{gevallen},

evalueer:

  1. f (-1)
  2. f (0)
  3. f (2)
Toon antwoord

1.f(x) is gedefinieerd als 7x+3 voor x=-1 omdat }-1<0.

Evalueer: f(-1)=7(-1)+3=-7+3=-4

2. f(x) is gedefinieerd als 7x+6 voor x=0{want0{0}.

Waarderen: f(0)=7(0)+6=0+6=6

3. f(x) is gedefinieerd als 7x+6 voor x=2{want2{0}.

Evalueer: f(2)=7(2)+6=14+6=20

In de volgende video laten we zien hoe je verschillende waarden kunt evalueren gegeven een stukgewijs gedefinieerde functie.

In het volgende voorbeeld laten we zien hoe we een functie evalueren die de kosten van gegevensoverdracht voor een telefoonbedrijf modelleert.

Voorbeeld

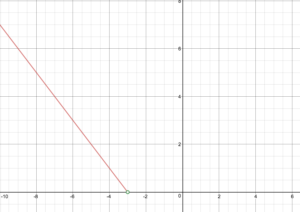
Een mobieletelefoonbedrijf gebruikt de onderstaande functie om de kosten, C, in dollars te bepalen voor g gigabytes gegevensoverdracht.

C(g)=begin{cases}{25}} } if }{ 0 }<{ g }<{ 2 }> 10g+5{ if }{ g}{ 2 }

Vind de kosten van het gebruik van 1.5 gigabyte aan gegevens en de kosten van het gebruik van 4 gigabyte aan gegevens.

Toon antwoord

Om de kosten te vinden van het gebruik van 1,5 gigabyte aan gegevens, C(1,5), kijken we eerst in welk deel van het domein onze invoer valt. Omdat 1,5 kleiner is dan 2, gebruiken we de eerste formule.

C(1,5) = $25

Om de kosten te vinden van het gebruik van 4 gigabytes aan gegevens, C(4), zien we dat onze invoer van 4 groter is dan 2, dus gebruiken we de tweede formule.

C(4)=10(4)+5=45

Analyse van de oplossing

De functie wordt weergegeven in de grafiek hieronder. We zien waar de functie verandert van een constante in een lijn met een positieve helling bij g=2. We plotten de grafieken voor de verschillende formules op een gemeenschappelijk stel assen, waarbij we ervoor zorgen dat elke formule op het juiste domein wordt toegepast.

C(g) = C(g)(g)(g)(rechts)=

Schrijf een stukgewijs gedefinieerde functie

In het laatste voorbeeld laten we zien hoe je een stukgewijs gedefinieerde functie kunt schrijven die de prijs van een rondleiding door een museum modelleert.

Voorbeeld

Een museum rekent $5 per persoon voor een rondleiding met een groep van 1 tot 9 personen of een vast bedrag van $50 voor een groep van 10 of meer personen. Schrijf een functie die het aantal mensen, n, relateert aan de kosten, C.

Toon antwoord

Twee verschillende formules zullen nodig zijn. Voor n-waarden onder 10, C=5n. Voor n-waarden die 10 of groter zijn, C=50.

C(n)=C(n)=begin{gevallen}{5n}50{ als}{0}<{n}<{10}50{ als}{n}>10{gevallen}

Analyse van de oplossing

De functie is weergegeven in figuur 21. De grafiek is een diagonale lijn van n=0 tot n=10 en daarna een constante. In dit voorbeeld komen de twee formules overeen op het ontmoetingspunt waar n=10, maar niet alle stapsgewijze functies hebben deze eigenschap.

In de volgende video laten we een voorbeeld zien van het schrijven van een stapsgewijs gedefinieerde functie gegeven een scenario.

Gegeven een stapsgewijze functie, schrijf de formule en identificeer het domein voor elk interval.

  1. Bepaal de intervallen waarvoor verschillende regels gelden.
  2. Bepaal formules die beschrijven hoe uit een ingang in elk interval een uitgang moet worden berekend.
  3. Gebruik accolades en if-statements om de functie te schrijven.

Graf Stuksgewijze functies

In dit gedeelte zullen we stuksgewijze functies plotten. De hieronder uitgezette functie vertegenwoordigt de kosten om gegevens over te brengen voor een bepaalde mobiele telefoonmaatschappij. We kunnen zien waar de functie verandert van een constante in een lijn met een positieve helling bij g=2. Bij het plotten van stukgewijze functies is het belangrijk om ervoor te zorgen dat elke formule op het juiste domein wordt toegepast. \In dit geval is de output 25 voor elke input tussen 0 en 2. Voor waarden gelijk aan of groter dan 2 is de uitvoer gedefinieerd als 10g+5.

Geef een stukgewijze functie, schets een grafiek.

  1. Geef op de x-as de grenzen aan van de intervallen op elk stuk van het domein.
  2. Geef voor elk stuk van het domein een grafiek op dat interval met behulp van de bijbehorende vergelijking voor dat stuk. Maak geen grafiek van twee functies over één interval, want dat zou in strijd zijn met de criteria van een functie.

Voorbeeld

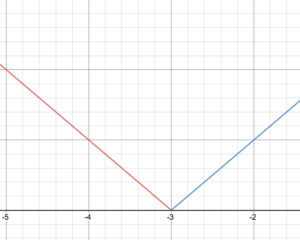
Schets een grafiek van de functie.

Gegeven de stukgewijze definitie f(x)=x – 3{begin}-x – 3{ als }x < -3{ x + 3{ als } x -3 -3 -eind{cases}
Teken de grafiek van f.
Bepaal het domein en het bereik van de functie.

Toon antwoord

Geef eerst een grafiek van de rechte f(x) = -x-3, waarbij je het deel waar x groter is dan -3 wegstreept. Plaats een open cirkel op (-3,0).

Plaats nu de rechte f(x) = x+3 op de grafiek, beginnend bij het punt (-3,0). Merk op dat voor dit deel van de grafiek het punt (-3,0) is inbegrepen, zodat u de open cirkel kunt verwijderen.

De twee grafieken ontmoeten elkaar in het punt (-3,0)

Het domein van deze functie is alle reële getallen omdat (-3,0)niet is inbegrepen als eindpunt van f(x) = -x-3, maar wel als eindpunt van f(x) = x+3.

Het bereik van deze functie begint bij f(x)=0 en omvat 0, en gaat tot oneindig, dus we zouden dit schrijven als x(x)=0

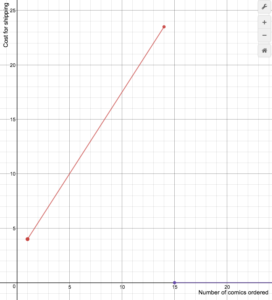
In het volgende voorbeeld zullen we een grafiek maken van een stuk voor stuk gedefinieerde functie die de verzendkosten voor een online verkoper van stripboeken modelleert.

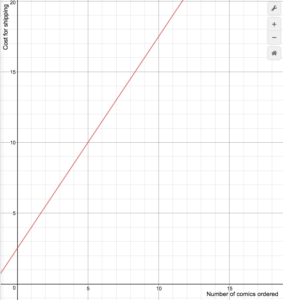
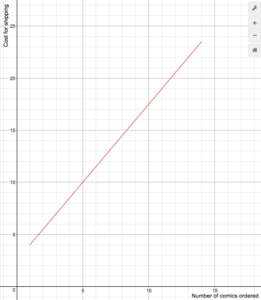
Voorbeeld

Een online verkoper van stripboeken berekent verzendkosten volgens de volgende formule

S(n)=>begin{gevallen}1,5n+2.5Teken een grafiek van de kostenfunctie.

Toon antwoord

Teken eerst de lijn S(n)=1,5n+2,5. We kunnen transformaties gebruiken: dit is een verticale uitrekking van de identiteit met een factor 1,5, en een verticale verschuiving met 2,5.

S(n)=1,5n+2.5

Nu kunnen we de delen van de grafiek elimineren die niet in het domein liggen op basis van 1<

S(n) = 1,5n+2,5 voor 1<=n<=14

Tot slot voegen we de constante functie S(n)=0 toe voor ingangen groter dan of gelijk aan 15. Zet gesloten punten op de uiteinden van de grafiek om aan te geven dat de eindpunten zijn opgenomen.

In de volgende video laten we zien hoe je een grafiek maakt van een stuk gedefinieerde functie die lineair is over beide domeinen.

Samenvatting

  • Een stukgewijze functie is een functie waarin meer dan één formule wordt gebruikt om de uitvoer over verschillende stukken van het domein te definiëren.
  • Evaluatie van een stukgewijze functie betekent dat u goed moet letten op de juiste uitdrukking die wordt gebruikt voor de gegeven invoer

Om stukgewijze functies te grafieken, moet u eerst vaststellen waar het domein is verdeeld. Grafiek functies op het domein met behulp van hulpmiddelen zoals plotten punten, of transformaties. Zorg ervoor dat u open of gesloten cirkels gebruikt op de eindpunten van elk domein, afhankelijk van of het eindpunt is inbegrepen.

Geef een antwoord

Het e-mailadres wordt niet gepubliceerd.