Half Adder en Full Adder Circuit
Half Adder en Full Adder circuits wordt uitgelegd met hun waarheidstabellen in dit artikel. Het ontwerp van een Full Adder met behulp van een Half Adder-schakeling wordt ook getoond. Single-bit Full Adder schakeling en Multi-bit optelling met behulp van Full Adder wordt ook getoond.
Voordat we dit onderwerp behandelen, is het zeer belangrijk om te weten wat Booleaanse logica en logische poorten inhouden.
LOOK : BOOLEAN LOGIC
LOOK : LOGIC GATES
LOOK : FLIP FLOPS
Wat is een opteller?
Een opteller is een soort rekenmachine die wordt gebruikt om twee binaire getallen bij elkaar op te tellen. Als ik zeg, rekenmachine, bedoel ik niet een met knoppen, dit is een schakeling die kan worden geïntegreerd met vele andere schakelingen voor een breed scala van toepassingen. Er zijn twee soorten adders;
- Half adder
- Volledige adder
Half adder
Met behulp van een halve adder kunnen we schakelingen ontwerpen die in staat zijn eenvoudige optellingen uit te voeren met behulp van logische poorten.
Laten we eerst eens kijken naar het optellen van enkele bits.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
Dit zijn de minst mogelijke combinaties van enkele bits. Maar het resultaat voor 1+1 is 10. Hoewel dit probleem kan worden opgelost met behulp van een EXOR Poort, moet het somresultaat als een 2-bits uitgang worden herschreven, als je toch om de uitgang geeft.
Dus kunnen de bovenstaande vergelijkingen worden geschreven als
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Hier wordt de uitgang ‘1’van ’10’ de carry-out. Het resultaat is weergegeven in een waarheidstabel hieronder. SUM’ is de normale uitgang en ‘CARRY’ is de carry-out.
INPUTS OUTPUTS
A B SUM CARRY
0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Vanuit de vergelijking, is het duidelijk dat deze 1-bit adder eenvoudig kan worden geïmplementeerd met behulp van een EXOR poort voor de uitgang ‘SUM’ en een AND poort voor de carry. Kijk eens naar de implementatie hieronder.
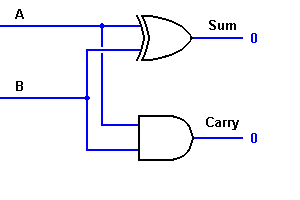
Voor complexe optelling kunnen er gevallen zijn waarin u twee 8-bits bytes bij elkaar moet optellen. Dit kan alleen met behulp van full-adder logica.
Full Adder
Dit type adder is iets moeilijker te implementeren dan een half-adder. Het belangrijkste verschil tussen een half-adder en een full-adder is dat de full-adder drie ingangen en twee uitgangen heeft. De eerste twee ingangen zijn A en B en de derde ingang is een carry-ingang, aangeduid als CIN. Wanneer een logische volledige adder is ontworpen, kunnen we er acht aan elkaar rijgen om een byte-wijde adder te maken en de carry-bit van de ene adder naar de volgende te cascaderen.
De carry-bit aan de uitgang wordt aangeduid als COUT en de normale uitgang wordt aangeduid als S. Kijk maar eens naar de waarheidstabel.
INPUTS OUTPUTS
A B CIN COUT S
0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 0
1 1 0 1 0
1 1 1 1 1
Vanuit de bovenstaande waarheids-tabel, kan de volledige adderlogica worden geïmplementeerd. We zien dat de uitgang S een EXOR is tussen de ingang A en de half-adder SUM uitgang met de ingangen B en CIN. We moeten ook opmerken dat de COUT alleen waar zal zijn als een van de twee ingangen van de drie HIGH is.
Dus kunnen we een volledige optelschakeling implementeren met behulp van twee halve optelschakelingen. De eerste halve opteller zal worden gebruikt om A en B op te tellen om een partiële som te produceren. De tweede halve adder logica kan worden gebruikt om CIN toe te voegen aan de Som die door de eerste halve adder wordt geproduceerd om de uiteindelijke S-uitgang te krijgen. Als een van de logica’s van de halve adder een carry produceert, zal er een carry naar de uitgang zijn. COUT is dus een OF-functie van de Carry-uitgangen van de halve adder. Kijk eens naar de implementatie van de volledige optellerschakeling hieronder.
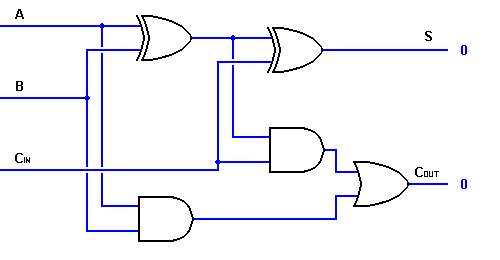
Hoewel de implementatie van grotere logische schema’s mogelijk is met de bovenstaande volledige optellogica, wordt meestal een eenvoudiger symbool gebruikt om de bewerking weer te geven. Hieronder staat een eenvoudiger schema voor een één-bits full adder.
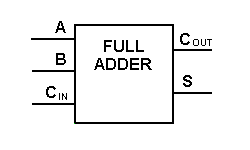
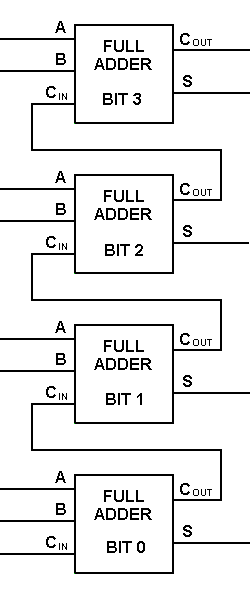
Met dit type symbool kunnen we twee bits bij elkaar optellen, waarbij we een carry nemen van de volgende lagere orde van grootte, en een carry naar de volgende hogere orde van grootte sturen. In een computer moet voor een multibitsbewerking elk bit worden voorgesteld door een volledige opteller en moet het tegelijkertijd worden opgeteld. Om twee 8-bitsgetallen op te tellen, zijn dus 8 volledige adders nodig, die kunnen worden gevormd door twee van de 4-bitsblokken in cascade te schakelen. De optelling van twee 4-bit getallen wordt hieronder getoond.