Voorafgaande – Maatregelen van Afstand in Data Mining
In Data Mining, verwijst de gelijkenismaat naar de afstand met dimensies die kenmerken van het gegevensobject, in een dataset vertegenwoordigen. Als deze afstand kleiner is, is er een hoge mate van overeenkomst, maar als de afstand groot is, is er een lage mate van overeenkomst.
Enkele van de populaire similariteitsmaten zijn –
- Euclidische afstand.
- Manhattan-afstand.
- Jaccard-gelijkenis.
- Minkowski-afstand.
- Cosine-gelijkenis.
Cosine-gelijkenis een metriek die behulpzaam is bij het bepalen, hoe gelijksoortig de gegevensobjecten zijn, ongeacht hun grootte. We kunnen de overeenkomst tussen twee zinnen in Python meten met behulp van cosinusgelijkheid. In cosinus gelijkenis, worden data objecten in een dataset behandeld als een vector. De formule om de cosinus gelijkheid tussen twee vectoren te vinden is –
Cos(x, y) = x . y / ||x|| * ||y||
waar,
- x . y = product (punt) van de vectoren ‘x’ en ‘y’.
- ||x|| en ||y|| = lengte van de twee vectoren ‘x’ en ‘y’.
- ||x| * ||y|| = kruisproduct van de twee vectoren ‘x’ en ‘y’.
Voorbeeld :
Bedenk een voorbeeld om de overeenkomst te vinden tussen twee vectoren – ‘x’ en ‘y’, met behulp van Cosinus Gelijkenis.
De vector ‘x’ heeft waarden, x = { 3, 2, 0, 5 }
De vector ‘y’ heeft waarden, y = { 1, 0, 0, 0 }
De formule voor het berekenen van de cosinus gelijkenis is : Cos(x, y) = x . y / ||x|| * ||y||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1∴ Cos(x, y) = 3 / (6.16 * 1) = 0.49
De dissimilariteit tussen de twee vectoren ‘x’ en ‘y’ wordt gegeven door –
∴ Dis(x, y) = 1 - Cos(x, y) = 1 - 0.49 = 0.51
- De cosinusgelijkenis tussen twee vectoren wordt gemeten in ‘θ’.
- Als θ = 0°, overlappen de vectoren ‘x’ en ‘y’ elkaar en zijn ze dus gelijksoortig.
- Als θ = 90°, zijn de vectoren ‘x’ en ‘y’ niet gelijksoortig.
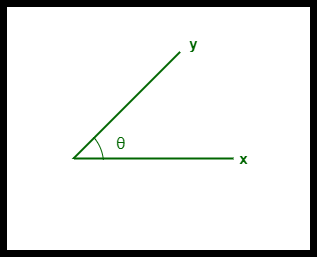
Cosinusovereenstemming tussen twee vectoren
Voordelen :
- De cosinusovereenstemming is voordelig omdat zelfs als de twee gelijksoortige gegevensobjecten ver van elkaar verwijderd zijn door de Euclidische afstand vanwege de grootte, ze toch een kleinere hoek tussen hen kunnen hebben. Hoe kleiner de hoek, hoe groter de overeenkomst.
- Wanneer uitgezet op een multidimensionale ruimte, geeft de cosinus gelijkenis de oriëntatie (de hoek) van de data objecten en niet de magnitude.