Laten we beginnen met het onderzoeken van het delen van waarden met exponenten.
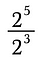
Houd in gedachten dat exponenten herhaalde vermenigvuldigingen voorstellen. We kunnen de bovenstaande uitdrukking dus herschrijven als:
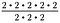
Sinds 2/2 = 1, heffen we drie reeksen van 2/2 op. Dan blijft over 2 – 2, of 2 in het kwadraat.
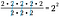
Natuurlijk kunnen we een kortere weg nemen en het aantal 2’en onderaan aftrekken van het aantal 2’en bovenaan. Aangezien deze hoeveelheden worden voorgesteld door hun respectieve exponenten, hoeven we alleen maar de gemeenschappelijke basis te schrijven met het verschil in exponentwaarden als de macht.
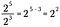
Als we deze regel veralgemenen, hebben we het volgende waarbij n een reëel getal zonder nul voorstelt en x en y ook reële getallen zijn.
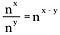
Verkenning van de nulde macht
Hieruit is eenvoudig af te leiden waarom elk getal dat niet tot de macht nul is verheven gelijk is aan 1. Laten we weer naar een concreet voorbeeld kijken.
We weten dat elk niet-nulgetal gedeeld door zichzelf gelijk is aan 1. Ik kan dus het volgende schrijven:
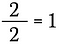
Dit is hetzelfde als schrijven:
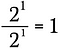
Nu zal ik de exponentregel van hierboven gebruiken om het linkerdeel van deze vergelijking te herschrijven.
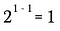
Dit is natuurlijk equivalent met:
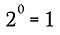
We kunnen hetzelfde proces gebruiken als in dit voorbeeld, samen met de veralgemeende regel hierboven, om aan te tonen dat elk reëel getal dat niet tot de macht nul is verheven, moet resulteren in 1.
Hoe zit het met nul tot de macht nul?
Dit is waar het lastig wordt. De bovenstaande methode breekt omdat, natuurlijk, delen door nul een no-no is. Laten we eens kijken waarom.
We beginnen met het bekijken van een veel voorkomende deler door nul fout.
Hoe zit het met 2÷0? Laten we eens kijken waarom we dit niet kunnen doen.
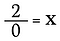
Deling is eigenlijk gewoon een vorm van vermenigvuldiging, dus wat gebeurt er als ik de bovenstaande vergelijking herschrijf als:
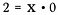
Welke waarde zou aan deze vergelijking voor x kunnen voldoen?
Er is geen waarde! Elk getal maal nul levert nul op, het kan nooit gelijk zijn aan 2. Daarom zeggen we dat delen door nul onbepaald is. Er is geen mogelijke oplossing.
Nu kijken we naar 0÷0.
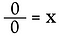
Herschrijf het opnieuw als een vermenigvuldigingsprobleem.
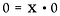
Hier hebben we te maken met een heel andere situatie. De oplossing voor x kan ELK reëel getal zijn! Er is geen manier om te bepalen wat x is. Daarom wordt 0/0 als onbepaald* beschouwd, niet als onbepaald.
Als we de bovenstaande methode proberen te gebruiken met nul als basis om te bepalen wat nul tot de macht nul zou zijn, komen we onmiddellijk tot stilstand en kunnen we niet verder omdat we weten dat 0÷0 ≠ 1, maar onbepaald is.
Wat is dan nul tot de macht nul?
Dit is zeer omstreden. Sommigen vinden dat het gedefinieerd moet worden als 1, terwijl anderen denken dat het 0 is, en weer anderen dat het niet gedefinieerd is. Er zijn goede wiskundige argumenten voor elk, en misschien is het het meest correct om het als onbepaald te beschouwen.
Ondanks dit is de wiskundige gemeenschap er voorstander van om nul tot de macht nul als 1 te definiëren, althans voor de meeste doeleinden.
Misschien is een nuttige definitie van exponenten voor de amateur-wiskundige als volgt: