De standaardformule om de determinant van een 3×3 matrix te vinden is een opsplitsing van kleinere 2×2 determinantproblemen die zeer eenvoudig te hanteren zijn. Als je een opfrisser nodig hebt, bekijk dan mijn andere les over het vinden van de determinant van een 2×2. Stel we krijgen een vierkante matrix A waarbij,
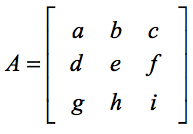
De determinant van matrix A wordt berekend als
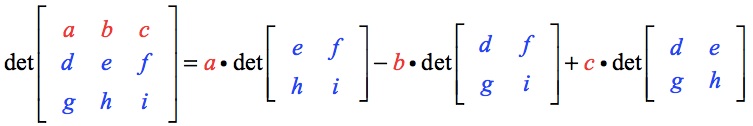
Hier volgen de kernpunten:
- Merk op dat de bovenste rij elementen namelijk a, b en c dienen als scalaire vermenigvuldigers naar een overeenkomstige 2bij-2 matrix.
- De scalaire a wordt vermenigvuldigd met de 2×2-matrix van overgebleven elementen die ontstaan wanneer verticale en horizontale lijnstukken worden getrokken die door a gaan.
- Hetzelfde proces wordt toegepast om de 2×2-matrices voor de scalaire multiplicatoren b en c te construeren.
Determinant van 3 x 3 Matrix (geanimeerd)

Voorbeelden van hoe de determinant van een 3×3 Matrix te vinden
Voorbeeld 1: Vind de determinant van onderstaande 3×3 matrix.
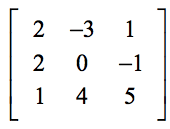
De onderstaande opzet helpt u de overeenkomst te vinden tussen de generieke elementen van de formule en de elementen van het eigenlijke probleem.
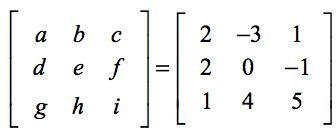
Toepassing van de formule,


Voorbeeld 2: Bepaal de determinant van de 3×3 onderstaande matrix.
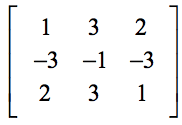
Wees heel voorzichtig bij het substitueren van de waarden op de juiste plaatsen in de formule. Veel voorkomende fouten treden op wanneer leerlingen onzorgvuldig worden bij de eerste stap van het substitueren van waarden.
Neem bovendien de tijd om ervoor te zorgen dat ook het rekenwerk correct is. Anders zal een enkele fout ergens in de berekening uiteindelijk een verkeerd antwoord opleveren.
Sinds,
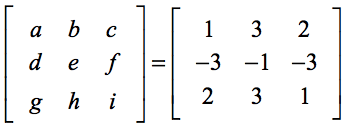
wordt onze berekening van de determinant…

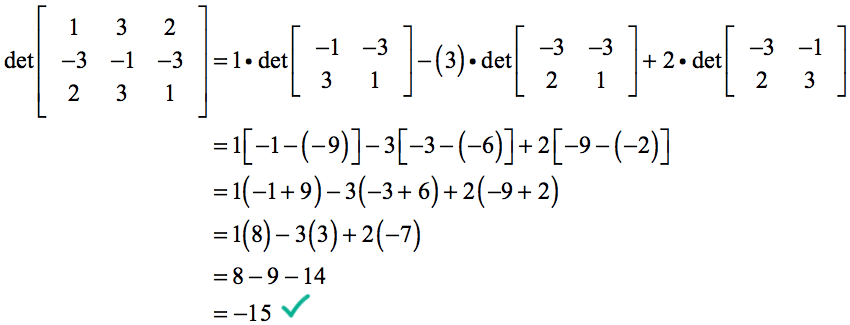
Voorbeeld 3: Los de determinant op van de 3×3 matrix hieronder.
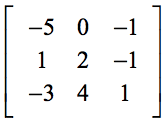
De aanwezigheid van nul (0) in de eerste rij zou onze berekening veel eenvoudiger moeten maken. Vergeet niet dat de elementen in de eerste rij fungeren als scalaire vermenigvuldigers. Daarom zal nul vermenigvuldigd met iets, de hele uitdrukking doen verdwijnen.