De verschillende soorten regelaars worden gebruikt om de prestaties van regelsystemen te verbeteren. In dit hoofdstuk bespreken we de basisregelaars zoals de proportionele, de afgeleide en de integrale regelaars.
Proportionele regelaar
De proportionele regelaar produceert een output, die evenredig is met het foutsignaal.
$$u(t) $
$$rechtse pijl u(t)=K_P e(t)$$
Toepassing van de Laplace-transformatie aan beide zijden –
$$U(s)=K_P E(s)$$
$$\frac{U(s)}{E(s)}=K_P$
Daaruit volgt, is de overdrachtsfunctie van de proportionele regelaar $K_P$.
Waar,
U(s) is de Laplace-transformatie van het actuatiesignaal u(t)
E(s) is de Laplace-transformatie van het foutsignaal e(t)
KP is de proportionaliteitsconstante
Het blokschema van het unity negative feedback closed loop regelsysteem samen met de proportionele regelaar is weergegeven in de volgende figuur.
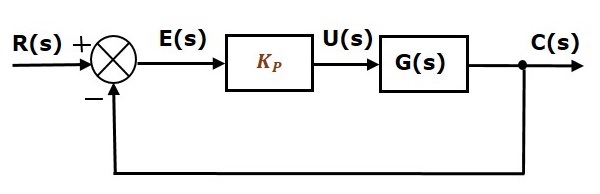
De proportionele regelaar wordt gebruikt om de transiëntresponsie volgens de behoefte te veranderen.
Derivatieve regelaar
De afgeleide regelaar produceert een uitgang, die een afgeleide is van het foutsignaal.
$$u(t)=K_D \frac{text{d}e(t)}{text{d}t}$$
Toepassen van de Laplace-transformatie aan beide zijden.
$$U(s)=K_D sE(s)$
$$\frac{U(s)}{E(s)}=K_D s$
Daaruit volgt dat de overdrachtsfunctie van de afgeleide regelaar $K_D s$ is.
Waarbij, $K_D$ de afgeleide constante is.
Het blokschema van het unity negative feedback closed loop regelsysteem samen met de afgeleide regelaar is weergegeven in de volgende figuur.
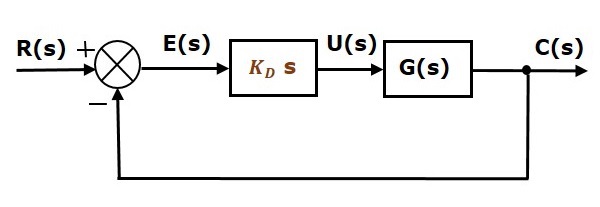
De afgeleide regelaar wordt gebruikt om van het instabiele regelsysteem een stabiel systeem te maken.
Integrale regelaar
De integrale regelaar produceert een uitgang, die integraal is van het foutsignaal.
$$u(t)=K_I \int e(t) dt$$
Toepassing van de Laplace-transformatie aan beide zijden –
$U(s)=\frac{K_I E(s)}{s}$
$$\frac{U(s)}{E(s)}=\frac{K_I}{s}$
Daaruit volgt, is de overdrachtsfunctie van de integrale regelaar $\frac{K_I}{s}$.
Waarbij $K_I$ de integrale constante is.
Het blokschema van het unity negative feedback closed loop regelsysteem samen met de integrale regelaar is weergegeven in de volgende figuur.
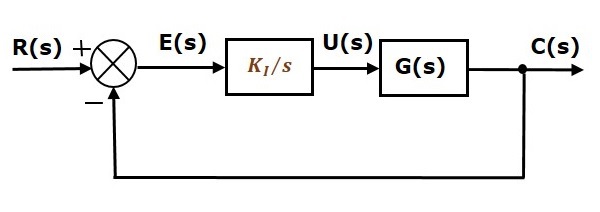
De integrale regelaar wordt gebruikt om de steady state error te verminderen.
Laten we het nu hebben over de combinatie van basisregelaars.
Proportioneel-afgeleide (PD) regelaar
De proportioneel-afgeleide regelaar produceert een output, die de combinatie is van de outputs van proportionele en afgeleide regelaars.
$$u(t)=K_P e(t)+K_D \frac{text{d}e(t)}{text{d}t}$$
Toepassing van de Laplace-transformatie aan beide zijden –
$$U(s)=(K_P+K_D s)E(s)$$
$$\frac{U(s)}{E(s)}=K_P+K_D s$$
Daaruit volgt, is de overdrachtsfunctie van de proportioneel-afgeleide regelaar $K_P + K_D s$.
Het blokschema van het unity negative feedback closed loop regelsysteem samen met de proportionele afgeleide regelaar is weergegeven in de volgende figuur.
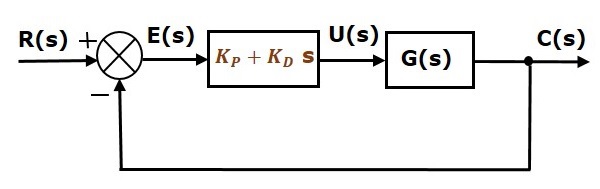
De proportionele afgeleide regelaar wordt gebruikt om de stabiliteit van het regelsysteem te verbeteren zonder de fout in de stationaire toestand te beïnvloeden.
Proportionele integrale (PI) regelaar
De proportionele integrale regelaar produceert een output, die de combinatie is van de outputs van de proportionele en integrale regelaars.
$$u(t)=K_P e(t)+K_I \int e(t) dt$$
Toepassing van de Laplace-transformatie aan beide zijden –
$$U(s)=links(K_P+\frac{K_I}{s} rechts )E(s)$$
$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$$
Daaruit volgt, is de overdrachtsfunctie van de proportionele integrale regelaar $K_P + \frac{K_I} {s}$.
Het blokschema van het unity negative feedback closed loop regelsysteem samen met de proportionele integrale regelaar is weergegeven in de volgende figuur.
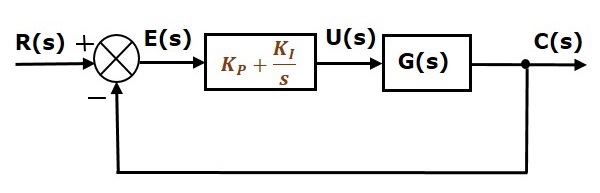
De proportionele integrale regelaar wordt gebruikt om de steady state error te verminderen zonder de stabiliteit van het regelsysteem te beïnvloeden.
Proportionele Integrale Afgeleide (PID) regelaar
De proportionele integrale afgeleide regelaar produceert een output, die de combinatie is van de outputs van proportionele, integrale en afgeleide regelaars.
$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{\text{d}e(t)}{\text{d}t}$$
Toepassing van de Laplace-transformatie aan beide zijden –
$$U(s)=links(K_P+\frac{K_I}{s}+K_D s rechts )E(s)$$
$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$
Daaruit volgt, is de overdrachtsfunctie van de proportioneel integraal afgeleide regelaar $K_P + \frac{K_I} {s} + K_D s$.
Het blokschema van het unity negative feedback closed loop regelsysteem samen met de proportionele integrale afgeleide regelaar is weergegeven in de volgende figuur.
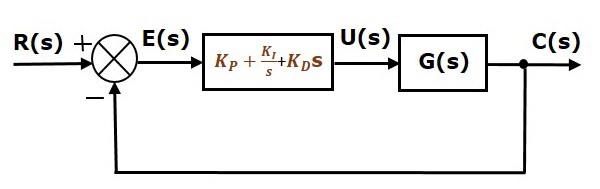
De proportionele integrale afgeleide regelaar wordt gebruikt om de stabiliteit van het regelsysteem te verbeteren en de steady state fout te verminderen.