ALGEMENE CHEMESTIE TOPICS
Energie: Fundamentele concepten
Vormen van energie: Kinetische en potentiële.Arbeid en energie.Warmte en temperatuur.Elektrostatische potentiële energie.
Energie: kinetische en potentiële
Het begrip energie is fundamenteel voor de natuurwetenschappen. Het is de bedoeling hier enkele eerste beginselen over energie uiteen te zetten en enkele vormen van energie te introduceren die van bijzonder belang zijn voor de chemie. Allereerst is het vaak zeer nuttig om een systeem te definiëren als een bepaald deel van het universum waarop onze waarnemingen worden gedaan. Het systeem bestaat uit een voorwerp of een verzameling voorwerpen, en onderscheidt zich van de rest van het heelal – dat wij de omgeving noemen – door een echte of denkbeeldige grens.
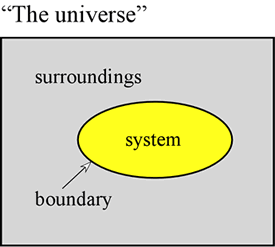
Een gasmonster in een vast volume, zoals een metalen cilinder, is een voorbeeld van een systeem – een systeem dat voor ons van belang zal zijn wanneer we de algemene eigenschappen van gassen gaan bestuderen. Andere voorbeelden zijn een gasmonster in een ballon of een verbrandingsmengsel in een cilinder met een zuiger. In beide gevallen is het systeem omsloten door een fysische, maar beweeglijke grens, zodat het volume van het systeem niet vast is. Een ander voorbeeld dat we vaak zullen bekijken is dat van een mengsel van stoffen in oplossing dat een chemische reactie ondergaat in een reageerbuis of een bekerglas. De hier geïntroduceerde terminologie is van bijzonder belang voor de studie van de wijze waarop energie zich in chemische systemen manifesteert, hetgeen grotendeels onder de noemer thermodynamica valt.
In de algemene chemie zijn de systemen die wij als relevant beschouwen gewoonlijk in rust en worden zwaartekrachtseffecten genegeerd. Vaak zijn wij het meest geïnteresseerd in systemen waarbinnen chemische reacties plaatsvinden, waarbij de chemische samenstelling van het systeem met de tijd verandert. Laten we echter voor het moment een breder perspectief aannemen door gebruik te maken van mechanische systemen zoals een slingerende slinger, of biljartballen die rollen en botsen, om ons te helpen algemene beginselen met betrekking tot energie te begrijpen.
Van een systeem kan worden gezegd dat het energie bezit op twee verschillende manieren, die we kinetische en potentiële energie noemen. Kinetische energie is de energie van materie in beweging. De natuurkunde geeft een exacte wiskundige definitie van kinetische energie (KE), weergegeven in de vergelijking (linksonder).
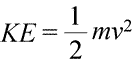
Hierin wordt de kinetische energie van een voorwerp voorgesteld als een product van de massa (m) van het voorwerp en het kwadraat van zijn snelheid (v), eveneens vermenigvuldigd met de constante ½. Indien het systeem uit meer dan één voorwerp bestaat, kan de totale kinetische energie worden uitgedrukt als een som van de kinetische energieën van de afzonderlijke voorwerpen.
Uit deze definitie kunnen wij eenheden voor energie afleiden. De SI-eenheid voor energie is de joule (J), die wordt gedefinieerd als:
1 J = 1 kg-m-s-2
Potentiële energie is de energie van een systeem die typisch kan worden omgezet in kinetische energie in een of andere vorm, en in staat is om, in een of andere mate, een hoeveelheid te produceren die arbeid wordt genoemd (hieronder verder besproken). Een duidelijk voorbeeld van potentiële energie is een baksteen op de richel van een gebouw. De baksteen heeft een zekere hoeveelheid potentiële energie op grond van zijn hoogte – zijn ligging ten opzichte van een gravitatieveld. Als we de baksteen een duwtje geven, zodat hij van de richel valt, beweegt hij spontaan in de richting van de lagere potentiële gravitatie-energie, en daarbij wint hij kinetische energie. Een ander voorbeeld is de elektrische potentiële energie van een batterij (die wordt uitgedrukt in spanning). Wanneer een stroomkring wordt gemaakt met een draad en een gloeilamp, die de twee aansluitingen van een batterij verbinden, veroorzaakt het verschil in elektrische potentiaal tussen beide elektronen in de draad om te bewegen (kinetische energie), resulterend in de productie van zowel warmte als licht.
Een belangrijk algemeen principe over energie is dat zij noch kan worden geschapen, noch kan worden vernietigd. Dit staat bekend als de wet van behoud van energie. Kwantitatief betekent dit dat in een systeem als de vallende steen of de slinger van een klok, de som van kinetische en potentiële energie constant is. Dit is enigszins een abstractie, omdat in een echte slinger voortdurend een deel van de energie verloren gaat door wrijving, en een kleine hoeveelheid energie aan de slinger moet worden toegevoegd om hem aan het slingeren te houden (en de klok te laten werken). Maar als we met zorgvuldige experimentele metingen rekening houden met dergelijke “verloren” energie (die in feite verschijnt als een toename van de warmte-energie van de omringende luchtmoleculen), dan blijkt dat energie inderdaad altijd behouden blijft. Een ander voorbehoud is samengevat in Einsteins beroemde vergelijking E = mc2, die een fundamentele gelijkwaardigheid van massa en energie uitdrukt. Een meer algemene vorm van de wet van behoud van energie, die de wet van behoud van massa-energie kan worden genoemd, verklaart deze gelijkwaardigheid. Terugkomend op de algemene scheikunde, dergelijke materie-energie omzettingen zijn niet typisch haar terrein, terwijl de studie van kernreacties en radioactiviteit onder de kernfysica valt.
Als we een chemische reactie beschouwen waarbij chemische veranderingen gepaard gaan met de productie van warmte, rijst de vraag: Hoe zit het in dit geval met behoud van energie? Het antwoord is dat er een vorm van potentiële energie is, die we chemische potentiële energie (of gewoon chemisch potentieel) kunnen noemen, en die we kunnen beschouwen als aanwezig in de moleculaire samenstelling van de reactanten. Deze potentiële energie wordt vervolgens omgezet in energie in de vorm van warmte, maar het blijkt dat de netto hoeveelheid aanwezige energie constant blijft, zodra wij in staat zijn de warmteproductie te definiëren en te meten. Een alledaags voorbeeld van wat wij nu kunnen begrijpen als chemische potentiële energie wordt gegeven door een benzinemotor, waarin het mengsel van benzine en zuurstof een latente vorm van energie bezit. Deze latente energie in het mengsel van benzine en zuurstof wordt gebruikt om de kinetische energie van een auto te produceren.
Werk en energie
Werk is een ander begrip dat een nauwkeurige definitie in de natuurkunde toelaat. Bovendien kunnen de wetten van de mechanica met energie in verband worden gebracht door middel van de werk-energietheorema. Een trap van een voetbal, of een aantal soortgelijke voorbeelden, illustreert het idee dat de kinetische energie van een voorwerp kan worden vergroot door toepassing van een kracht. De werk-energiethese, die een veralgemening van dit idee is, kan ruwweg als volgt worden gesteld: De verandering in de energie die een voorwerp bezit, is gelijk aan de grootte van de kracht die erop werkt, vermenigvuldigd met de afstand waarover de kracht werkt.
De energieverandering die in een systeem optreedt als gevolg van arbeid kan positief of negatief zijn, vanuit het standpunt van het systeem. Arbeid kan door een systeem worden verricht, of er kan arbeid op worden verricht door de omgeving. Als een systeem arbeid verricht, verliest het energie aan de omgeving. Als er arbeid op het systeem wordt verricht, neemt de energie van het systeem toe. Wanneer bijvoorbeeld een vonk in een cilinder met een beweegbare zuiger een verbrandingsmengsel doet ontbranden en het systeem snel uitzet, en de uitzetting mechanisch gekoppeld is aan de beweging van een stang in de omgeving, verricht het systeem van de cilinder arbeid op de omgeving, en verliest het daarbij energie. Dit is natuurlijk een deel van de manier waarop een verbrandingsmotor chemische potentiële energie omzet in de kinetische energie van een rijdende auto.
Eén implicatie van de arbeid-energietheorema betreft de eenheden, namelijk dat arbeid in dezelfde eenheden kan worden gemeten als energie. Aangezien de tweede wet van Newton kracht = massa × versnelling is, wordt de newton (N), de SI-eenheid voor kracht, afgeleid als M × L × T -2, en dus 1 N = 1 kg m s-2. Kracht maal afstand heeft de grootheden M × L2 × T -2, en dus is de SI-eenheid voor energie, de joule (J), gedefinieerd als 1 J = 1 kg m2 s-2. Op dit punt moet je voor jezelf nagaan dat de vergelijking voor kinetische energie dezelfde combinatie van de fundamentele grootheden massa (M), lengte (of afstand, L) , en tijd (T) impliceert.
Warmte en temperatuur
We gebruiken de woorden warmte en temperatuur vrij vaak, en spreken vaak over warmte als een vorm van energie. We hebben allemaal een intuïtief gevoel van wat deze dingen zijn, maar hier willen we er meer wetenschappelijk over nadenken, en ze meer formele definities geven als we kunnen. Dit is een noodzakelijke opmaat naar de kwantificering van de energie die overeenkomt met warmte, en vandaar naar metingen om de wet van behoud van energie te verifiëren. De warmte-energie van een systeem kan worden gelijkgesteld met de totale kinetische energie (zoals hierboven gedefinieerd) van de atomen en moleculen waaruit het is opgebouwd. De temperatuur van een voorwerp of systeem is in feite een maat voor de gemiddelde kinetische energie van de samenstellende atomen en/of moleculen. (N.B. De temperatuur is niet precies gelijk aan de gemiddelde kinetische energie van de moleculen, maar is er wel recht evenredig mee. Voor meer details, zie de kinetische moleculaire theorie webpagina).
Een manier om te visualiseren wat we bedoelen met warmte en temperatuur, en het onderscheid tussen beide, is een biljartbal-analogie te overwegen. In sommige eenvoudige contexten is het gedrag van biljartballen een adequaat model voor een verzameling atomen of moleculen, zoals in een monster van een gas. Net als biljartballen die zojuist zijn geraakt door een snel bewegende cue-bal, bewegen de moleculen van een gas in het rond, stuiteren op elkaar en op de wanden van de container waarin ze zich bevinden. De totale kinetische energie van de biljartballen, die slechts de som is van de afzonderlijke kinetische energieën van elke bal, is analoog aan de thermische energie-inhoud van een monster van gasmoleculen. In een “break” aan het begin van een biljartspel wordt de initiële kinetische energie van de cue-bal verdeeld over alle ballen op de tafel. Sommige ballen bewegen vrij snel, andere niet zo snel, maar de analogie met “warmte” of “thermische energie” voor het systeem van biljartballen is gewoon de som van deze kinetische energieën. Anderzijds zou de temperatuur van het biljartbalsysteem evenredig zijn met de gemiddelde kinetische energie van het geheel van ballen.
Elektrostatische potentiële energie
De wet van elektrostatische aantrekking en afstoting, of de Wet van Coulomb, beschrijft de kracht die wordt uitgeoefend op een geladen voorwerp als gevolg van de aanwezigheid van een ander geladen voorwerp. De kracht is het gemakkelijkst te berekenen wanneer de ladingen als zeer kleine puntladingen kunnen worden behandeld. De grootte van kracht een geladen voorwerp “voelt” is evenredig aan het product van de lasten (de SI-eenheid voor elektrische last is Coulomb, C), en omgekeerd evenredig aan het vierkant van de afstand van scheiding tussen de lasten (r in de figuur bij recht). De kracht is aantrekkelijk (zoals de zwaartekracht, en in de figuur aangegeven met naar binnen gerichte pijlpunten) als de ladingen tegengesteld van teken zijn, en afstotend als de ladingen hetzelfde teken hebben.
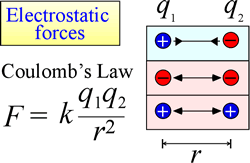
Wanneer krachten (zoals elektrostatische, magnetische en gravitatiekrachten) op afstand (door de ruimte, zonder mechanisch contact) kunnen werken, wordt van de voorwerpen die aan dergelijke krachten onderworpen zijn, gezegd dat zij zich in een potentieel energieveld bevinden. Wij spraken hierboven over gravitationele potentiële energie, en evenzo in het geval van elektrostatische krachten, zal een geladen voorwerp elektrostatische potentiële energie hebben op grond van zijn plaats in een elektrisch veld. Een dergelijk veld bestaat in de nabijheid van elke andere lading of ladingen.
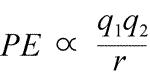
Vergelijking voor elektrostatische potentiële energie: PE is evenredig met de ladingen q1 en q2, en omgekeerd evenredig met de scheidingsafstand, r. De vorm van de potentiële energiefunctie volgt wiskundig uit de krachtuitdrukking, de Wet van Coulomb.
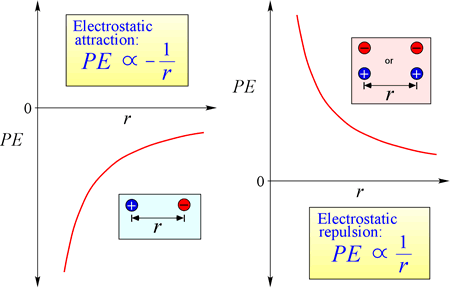
Gezien de tegengestelde tekens van ladingen in aantrekkingskracht, is de potentiële energie altijd negatief, en hoe dichter de ladingen elkaar naderen, hoe negatiever – d.w.z. hoe lager – de potentiële energie wordt. Als de scheidingsafstand, r nul nadert, wordt de potentiële energie oneindig negatief. Voor ladingen van hetzelfde teken is de afstotingsenergie altijd positief, en wordt oneindig positief als de scheidingsafstand, r nadert tot nul.
Electrostatische potentiële energie is een belangrijke overweging in de chemie. Een goed begrip van de aard van het atoom, de chemische binding en de intermoleculaire krachten is absoluut afhankelijk van het in rekening brengen van de invloed van lading-lading interacties die bijdragen aan de energie van een systeem.
Belangrijke eenheden
Energie (SI-eenheid) 1 joule = 1 J = 1 kg-m-s-2
Elementaire lading, e = 1,60218 × 10-19 C (coulomb, C)
Faraday constante: F = NAe = 9,64853 × 104 C-mol-1
Elektrische potentiaal: volt, V 1 V = 1 J C-1