Het gebeurt niet vaak dat een wiskundige vergelijking de nationale pers haalt, nog minder de populaire radio haalt, of, wat nog verbazingwekkender is, het onderwerp is van een debat in het Britse parlement. Maar in 2003 was de goede oude kwadratische vergelijking, waarover we allemaal op school hebben geleerd, al die dingen.
Waar we beginnen

Het begon allemaal op een vergadering van de National Union of Teachers. De kwadratische vergelijking werd de natie voorgehouden als voorbeeld van de wrede marteling die wiskundigen uitoefenden op arme nietsvermoedende schoolkinderen. Geïntrigeerd door deze beschuldiging kreeg de kwadratische vergelijking een hoofdrol op prime time radio, waar zij werd ondervraagd door een formidabele interviewer die meer gewend was het op te nemen tegen de premier. De (Londense) Times nam ruimte in haar leader column, die gewoonlijk meer gereserveerd is voor gewichtige discussies over de morele (of anderszins) gezondheid van de moderne wereld, om te verkondigen dat de vierkantsvergelijking nutteloos was, wiskunde nutteloos was en dat toch niemand wiskunde wilde studeren, dus waarom zou men zich druk maken. Bezorgd dat gevaarlijke beweringen van de kwadratische vergelijking onweersproken zouden blijven, werd in het Britse Lagerhuis gedebatteerd over het vitale belang van de vergelijking voor het voortbestaan van het Verenigd Koninkrijk (er werd een positief standpunt ingenomen, wellicht verheugt het u te weten).
Waar zou het allemaal eindigen? Was de kwadratische vergelijking echt dood? Kon het iemand iets schelen? Zijn wiskundigen echt kwaadaardige monsters die alleen kwadratische vergelijkingen aan een jongere generatie willen opdringen als middel om hun onsterfelijke zielen te corrumperen?
Misschien wel, maar het is niet echt de schuld van de kwadratische vergelijking. In feite heeft de kwadratische vergelijking een centrale rol gespeeld, niet alleen in de hele menselijke beschaving zoals wij die kennen, maar ook in de mogelijke opsporing van andere buitenaardse beschavingen en zelfs in zulke vitale moderne activiteiten als het kijken naar satelliettelevisie. Wat anders, afgezien van de aard van de goddelijke openbaring, zou kunnen worden geacht een dergelijke invloed te hebben gehad op het leven zoals wij dat kennen? Inderdaad, in zeer reële zin kunnen kwadratische vergelijkingen uw leven redden.
De Babyloniërs
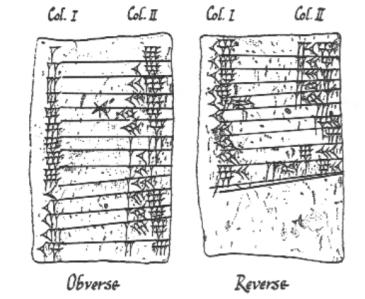
Babylonische spijkerschrifttabletten waarop de 9 maal tafels zijn vastgelegd
Het begon allemaal rond 3000 v.Chr. met de Babyloniërs. Zij waren een van ’s werelds eerste beschavingen, en kwamen met grootse ideeën zoals landbouw, irrigatie en schrijven. Zij tekenden de banen van de zon, de maan en de planeten en legden die vast op kleitabletten (die nog steeds in het British Museum te zien zijn). Aan de Babyloniërs danken wij de moderne ideeën over hoeken, waaronder de manier waarop de cirkel in 360 graden is verdeeld (als gevolg van een kleine rekenfout, één per dag). Wij danken de Babyloniërs ook voor de minder aangename uitvinding van de (gevreesde) belastingman. En dit was een van de redenen dat de Babyloniërs kwadratische vergelijkingen moesten oplossen.
Stelt u zich eens voor dat u een Babylonische boer bent. Ergens op je boerderij heb je een vierkant veld waarop je een of ander gewas verbouwt. Hoeveel van uw gewas kunt u op het veld verbouwen? Verdubbel de lengte van elke zijde van het veld en je ontdekt dat je vier keer zoveel van het gewas kunt verbouwen als voorheen. De reden hiervoor is dat de hoeveelheid gewas die je kunt verbouwen evenredig is met de oppervlakte van het veld, die op zijn beurt evenredig is met het kwadraat van de lengte van de zijde. In wiskundige termen: als  de lengte van de zijde van het veld is,
de lengte van de zijde van het veld is, 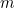 de hoeveelheid gewas die je kunt verbouwen op een vierkant veld met zijlengte 1, en
de hoeveelheid gewas die je kunt verbouwen op een vierkant veld met zijlengte 1, en  de hoeveelheid gewas die je kunt verbouwen, dan is
de hoeveelheid gewas die je kunt verbouwen, dan is
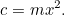 |
Dit is onze eerste kwadratische vergelijking, naakt en knipperend in het zonlicht. Kwadratische vergelijkingen en oppervlaktes zijn met elkaar verbonden als broers en zussen in dezelfde familie. Maar op dit moment hoeven we niets op te lossen – totdat de belastingman komt, dat wil zeggen! Vrolijk zegt hij tegen de boer: “Ik wil dat u mij gewassen geeft om de belastingen op uw boerderij te betalen.” De boer staat nu voor een dilemma: hoe groot is het veld dat hij nodig heeft om die hoeveelheid gewas te verbouwen? Wij kunnen deze vraag gemakkelijk beantwoorden, in feite
gewassen geeft om de belastingen op uw boerderij te betalen.” De boer staat nu voor een dilemma: hoe groot is het veld dat hij nodig heeft om die hoeveelheid gewas te verbouwen? Wij kunnen deze vraag gemakkelijk beantwoorden, in feite
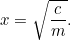 |
Het vinden van vierkantswortels met behulp van een rekenmachine is voor ons gemakkelijk, maar was meer een probleem voor de Babyloniërs. In feite ontwikkelden zij een methode van opeenvolgende benaderingen van het antwoord die identiek is aan het algoritme (de Newton-Raphson methode genoemd) dat door moderne computers wordt gebruikt om veel moeilijker problemen dan kwadratische vergelijkingen op te lossen.
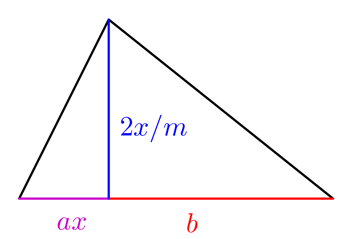
Nu zijn niet alle akkers vierkant. Laten we nu eens veronderstellen dat de boer een meer vreemd gevormde akker heeft met twee driehoekige doorsneden, zoals hiernaast is weergegeven.
Voor de juiste waarden van  en
en 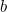 wordt de hoeveelheid gewas die de boer op dit veld kan verbouwen gegeven door
wordt de hoeveelheid gewas die de boer op dit veld kan verbouwen gegeven door
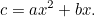 |
Dit lijkt een stuk meer op de kwadratische vergelijking die we gewend zijn, en zelfs onder het kwade oog van de belastingman, is het een stuk moeilijker op te lossen. Toch kwamen de Babyloniërs weer met het antwoord. Eerst delen we door  om
om
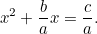 |
Nu maken we het kwadraat compleet door gebruik te maken van het feit dat
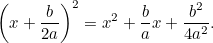 |
Als we dit combineren met de oorspronkelijke vergelijking krijgen we
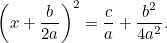 |
Dit is nu een vergelijking die we kunnen oplossen door vierkantswortels te nemen. Het resultaat is de beroemde “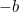 formule”:
formule”:
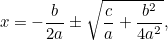 |
die kan worden herschreven als
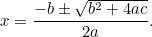 |
(De formule heeft meestal “-4ac” omdat de kwadratische vergelijking meestal in de vorm “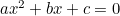 ” wordt geschreven.)
” wordt geschreven.)
Het feit dat het nemen van een vierkantswortel een positief of een negatief antwoord kan geven, leidt tot het opmerkelijke resultaat dat een kwadratische vergelijking twee oplossingen heeft. Tot zover de wiskundige puzzels met slechts één oplossing!
Nu, dit is waar het onderwijs van kwadratische vergelijkingen vaak ophoudt. We zijn aangeland bij dat voorwerp dat alle journalisten zo geliefd maken als ze wiskundigen interviewen – een formule. Er kunnen eindeloos veel vragen worden verzonnen waarbij 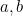 en
en  in de formule moeten worden gestopt om (twee) antwoorden te krijgen. Maar dit is helemaal niet waar wiskunde over gaat. Het vinden van een formule is slechts de eerste stap op een lange weg. We moeten ons afvragen: wat betekent de formule; wat vertelt ze ons over het universum; is het hebben van een formule werkelijk van belang? Laten we nu eens kijken waar deze formule ons zal brengen.
in de formule moeten worden gestopt om (twee) antwoorden te krijgen. Maar dit is helemaal niet waar wiskunde over gaat. Het vinden van een formule is slechts de eerste stap op een lange weg. We moeten ons afvragen: wat betekent de formule; wat vertelt ze ons over het universum; is het hebben van een formule werkelijk van belang? Laten we nu eens kijken waar deze formule ons zal brengen.
Een verrassing voor de Grieken, een beetje wiskundige origami en gevoel voor verhoudingen
We spoelen nu 1000 jaar vooruit naar de Oude Grieken en zien wat zij van kwadratische vergelijkingen maakten. De Grieken waren uitstekende wiskundigen en ontdekten veel van de wiskunde die wij vandaag nog gebruiken. Een van de vergelijkingen die zij graag wilden oplossen was de (eenvoudige) kwadratische vergelijking
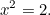 |

Zij wisten dat deze vergelijking een oplossing had. In feite is het de lengte van de schuine zijde van een rechthoekige driehoek met zijden van lengte één.
Uit de stelling van Pythagoras volgt dat als een rechthoekige driehoekhoekige driehoek kortere zijden  en
en  heeft en schuine zijde
heeft en schuine zijde  dan
dan
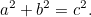 |
Als men 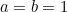 en
en  zet dan
zet dan 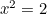 . Dus
. Dus 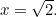
Wat is  in dit geval? Of, om de vraag te stellen die de Grieken stelden, wat voor soort getal is het? De reden dat dit van belang was, lag in het gevoel voor verhoudingen dat de Grieken hadden. Zij geloofden dat alle getallen in verhouding tot elkaar stonden. Om precies te zijn betekende dit dat alle getallen breuken waren van de vorm
in dit geval? Of, om de vraag te stellen die de Grieken stelden, wat voor soort getal is het? De reden dat dit van belang was, lag in het gevoel voor verhoudingen dat de Grieken hadden. Zij geloofden dat alle getallen in verhouding tot elkaar stonden. Om precies te zijn betekende dit dat alle getallen breuken waren van de vorm 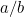 waarbij
waarbij  en
en  gehele getallen zijn. Getallen als 1/2, 3/4 en 355/113 zijn allemaal voorbeelden van breuken. Het lag voor de hand te verwachten dat
gehele getallen zijn. Getallen als 1/2, 3/4 en 355/113 zijn allemaal voorbeelden van breuken. Het lag voor de hand te verwachten dat  ook een breuk was. De grote verrassing was dat dat niet zo is. In feite is
ook een breuk was. De grote verrassing was dat dat niet zo is. In feite is
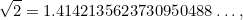 |
waarbij de puntjes  betekenen dat de decimale uitbreiding van
betekenen dat de decimale uitbreiding van  doorgaat tot in het oneindige zonder enig waarneembaar patroon. (We zullen deze situatie later weer tegenkomen als we over chaos leren.)
doorgaat tot in het oneindige zonder enig waarneembaar patroon. (We zullen deze situatie later weer tegenkomen als we over chaos leren.)
 was het eerste irrationele getal (d.w.z. een getal dat geen breuk, of rationaal is) dat als zodanig werd erkend. Andere voorbeelden zijn
was het eerste irrationele getal (d.w.z. een getal dat geen breuk, of rationaal is) dat als zodanig werd erkend. Andere voorbeelden zijn 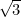 ,
,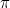 ,
,  en in feite “de meeste” getallen. Het duurde tot de 19e eeuw voordat we een goede manier hadden om over deze getallen na te denken. De ontdekking dat
en in feite “de meeste” getallen. Het duurde tot de 19e eeuw voordat we een goede manier hadden om over deze getallen na te denken. De ontdekking dat  geen rationeel getal was, veroorzaakte zowel grote opwinding (100 ossen werden geofferd als gevolg) als grote schok, waarbij de ontdekker zelfmoord moest plegen. (Laat dit een vreselijke waarschuwing zijn voor de wiskundigen!) Op dit punt gaven de Grieken de algebra op en wendden zich tot de meetkunde.
geen rationeel getal was, veroorzaakte zowel grote opwinding (100 ossen werden geofferd als gevolg) als grote schok, waarbij de ontdekker zelfmoord moest plegen. (Laat dit een vreselijke waarschuwing zijn voor de wiskundigen!) Op dit punt gaven de Grieken de algebra op en wendden zich tot de meetkunde.
Voorwaar geen obscuur getal, we komen  regelmatig tegen: telkens wanneer we een stuk A4 papier gebruiken. In Europa worden papiermaten gemeten in A-maten, waarbij A0 de grootste is met een oppervlakte van
regelmatig tegen: telkens wanneer we een stuk A4 papier gebruiken. In Europa worden papiermaten gemeten in A-maten, waarbij A0 de grootste is met een oppervlakte van 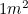 . De A-maten hebben een speciale onderlinge verhouding. Als we nu een beetje origami doen, waarbij we een vel A1-papier dubbelvouwen (langs de langste zijde), krijgen we A2-papier. Nogmaals dubbelvouwen geeft A3, en nog een keer geeft A4 enz. Het papier is echter zo ontworpen dat de verhouding van elk van de A-formaten hetzelfde is – dat wil zeggen dat elk stuk papier dezelfde vorm heeft.
. De A-maten hebben een speciale onderlinge verhouding. Als we nu een beetje origami doen, waarbij we een vel A1-papier dubbelvouwen (langs de langste zijde), krijgen we A2-papier. Nogmaals dubbelvouwen geeft A3, en nog een keer geeft A4 enz. Het papier is echter zo ontworpen dat de verhouding van elk van de A-formaten hetzelfde is – dat wil zeggen dat elk stuk papier dezelfde vorm heeft.
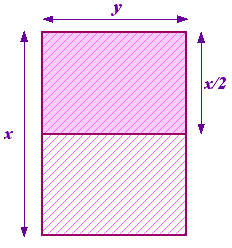
We kunnen de vraag stellen welke verhouding dit is. Begin met een stuk papier met zijden x en y, waarbij x de langste zijde is. Deel dit nu in tweeën zodat je weer een stuk papier krijgt met zijden y en x/2 waarbij nu y de langste zijde is. Dit is hiernaast geïllustreerd.
De verhoudingen van het eerste stuk papier zijn 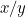 en die van het tweede
en die van het tweede 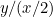 of
of 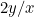 . We willen dat deze twee verhoudingen gelijk zijn. Dit betekent dat
. We willen dat deze twee verhoudingen gelijk zijn. Dit betekent dat
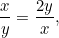 |
of
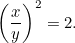 |
Nog een kwadratische vergelijking! Gelukkig is het er een die we al eerder zijn tegengekomen. Als we die oplossen, vinden we dat
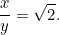 |
Dit resultaat is gemakkelijk te controleren. Neem gewoon een vel A4-papier (of A3- of A5-papier) en meet de zijden. We kunnen ook de grootte van elk vel berekenen. De oppervlakte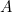 van een stuk A0-papier wordt gegeven door
van een stuk A0-papier wordt gegeven door
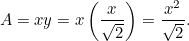 |
Maar we weten dat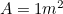 dus hebben we nog een kwadratische vergelijking voor de langste zijde
dus hebben we nog een kwadratische vergelijking voor de langste zijde van A0, gegeven door
van A0, gegeven door
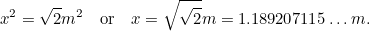 |
Dit betekent dat de langste zijde van A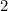 wordt gegeven door
wordt gegeven door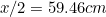 (waarom?) en die van A
(waarom?) en die van A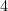 door
door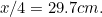 . Controleer deze op je eigen vellen papier.
. Controleer deze op je eigen vellen papier.
Het papier dat in de Verenigde Staten wordt gebruikt, foolscap genoemd, heeft een andere verhouding. Om te zien waarom, gaan we terug naar de Grieken en een andere kwadratische vergelijking. De kwadratische vergelijking heeft zoveel ellende veroorzaakt, maar heeft zichzelf verlost in de zoektocht naar de perfecte verhoudingen: een zoektocht die nog steeds voortduurt bij het ontwerpen van filmsets, en die in veel aspecten van de natuur te zien is.
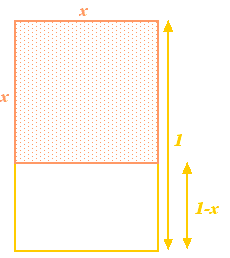
Laten we beginnen met een rechthoek, en dan daaruit een vierkant verwijderen met dezelfde zijde als de kortste zijde van de rechthoek. Als de langste zijde van de rechthoek lengte 1 heeft en de kortste zijde lengte  , dan heeft het vierkant zijden van lengte
, dan heeft het vierkant zijden van lengte  . Verwijdering uit de rechthoek geeft een kleinere rechthoek met langste zijde
. Verwijdering uit de rechthoek geeft een kleinere rechthoek met langste zijde  en kleinste zijde
en kleinste zijde 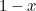 . Tot zover, zo abstract. De Grieken geloofden echter dat de rechthoek met de meest esthetische verhoudingen (de zogenaamde Gulden Rechthoek) de rechthoek was waarvoor de grote en de kleine rechthoek die hierboven geconstrueerd zijn, dezelfde verhoudingen hebben. Om dit mogelijk te maken moeten we
. Tot zover, zo abstract. De Grieken geloofden echter dat de rechthoek met de meest esthetische verhoudingen (de zogenaamde Gulden Rechthoek) de rechthoek was waarvoor de grote en de kleine rechthoek die hierboven geconstrueerd zijn, dezelfde verhoudingen hebben. Om dit mogelijk te maken moeten we
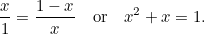 |
Dit is weer een kwadratische vergelijking: een zeer belangrijke die in allerlei toepassingen voorkomt. Ze heeft de (positieve) oplossing
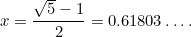 |
Het getal  wordt de gulden snede genoemd en wordt vaak aangeduid met de Griekse letter
wordt de gulden snede genoemd en wordt vaak aangeduid met de Griekse letter 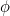 .
.

De Gulden Rechthoek is te zien in de vorm van ramen, vooral op Georgische huizen. Meer recent is de Gulden Snede ook terug te vinden als de “perfecte vorm” voor foto’s en filmbeelden. De kwadratische vergelijking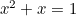 komt ook voor in studies van de populaties van konijnen en in het patroon waarin de zaden van zonnebloemen en de bladeren aan de stengels van planten zijn gerangschikt. Deze zijn allemaal verbonden met de Gulden Snede via de Fibonacci-reeks die gegeven wordt door
komt ook voor in studies van de populaties van konijnen en in het patroon waarin de zaden van zonnebloemen en de bladeren aan de stengels van planten zijn gerangschikt. Deze zijn allemaal verbonden met de Gulden Snede via de Fibonacci-reeks die gegeven wordt door
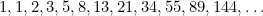 |

Zonnebloemzaden, gerangschikt volgens de getallen van Fibonacci |
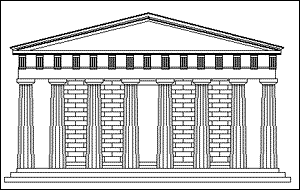
Het Parthenon, dat de Gulden Snede belichaamt |
In deze reeks is elke term de som van de twee vorige termen. Fibonacci ontdekte het in de 15e eeuw in een poging om de toekomstige populatie konijnen te voorspellen. Als je de verhouding van elke term tot de term erna neemt, krijg je de getallenreeks
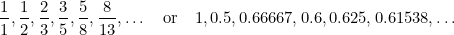 |
en deze getallen komen steeds dichter bij (je raadt het al) de Gulden Snede 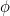 .
.
Door beide wortels van bovenstaande kwadratische vergelijking te vinden, kunnen we een formule vinden voor de n-de term in de Fibonacci-reeks. Als  het
het 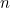 ste getal is met
ste getal is met 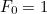 en
en 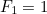 dan wordt
dan wordt  gegeven door de formule
gegeven door de formule
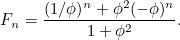 |
Conics verbinden kwadratische vergelijkingen met de sterren

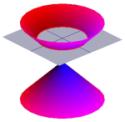
De Grieken waren ook zeer geïnteresseerd in de vorm van kegels. De afbeelding links toont een typische kegel.
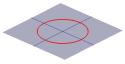
De helft van de kegel kan worden gevisualiseerd als de verspreiding van het licht van een fakkel. Als je nu met een zaklamp op een plat oppervlak zoals een muur schijnt, zul je verschillende vormen zien als je de zaklamp beweegt. Deze vormen worden kegelsneden genoemd en zijn de krommen die je krijgt als je onder verschillende hoeken een snee door een kegel maakt. Juist deze krommen werden door de Grieken bestudeerd, en zij erkenden dat er in principe vier soorten kegelsneden waren. Als je een horizontale doorsnede door de kegel neemt, krijg je een cirkel. Een doorsnede onder een kleine hoek met de horizontaal geeft een ellips. Neem je een verticale doorsnede dan krijg je een hyperbool en neem je een doorsnede evenwijdig aan één zijde van de kegel dan krijg je een parabool. Deze krommen zijn hieronder geïllustreerd.
 |
 |
 |
 |
 |
 |
 |
 |

Een doorsnededoorsnede van een kegel kan een cirkel zijn … |

… een ellips … |
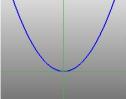
… een parabool … |
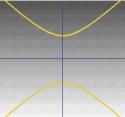
…. of een hyperbool. |
Conische doorsneden komen in ons verhaal omdat elk van hen wordt beschreven door een kwadratische vergelijking. In het bijzonder, als 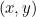 een punt op elke kromme voorstelt, dan verbindt een kwadratische vergelijking
een punt op elke kromme voorstelt, dan verbindt een kwadratische vergelijking  en
en 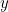 . We hebben:
. We hebben:
De cirkel: 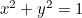 ;
;
De ellips: 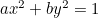 ;
;
De hyperbool: 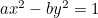 ;
;
De parabool: 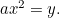
Deze krommen waren sinds de Grieken bekend en bestudeerd, maar afgezien van de cirkel leken zij geen praktische toepassing te hebben. Zoals we in het volgende nummer van Plus zullen zien, leidde een verband tussen kwadratische vergelijkingen en kegelsneden, in combinatie met een enorme meevaller, tot een beter begrip van de werking van het heelal, en in de 16e eeuw was het tijd voor kegelsneden om de wereld te veranderen.
Over de auteurs
Chris Budd is hoogleraar toegepaste wiskunde in het departement wiskundige wetenschappen aan de universiteit van Bath, en de leerstoel wiskunde aan het Royal Institution in Londen.
Chris Sangwin is staflid aan de School of Mathematics and Statistics van de universiteit van Birmingham. Hij is een Research Fellow in het Learning and Teaching Support Network centre for Mathematics, Statistics, and Operational Research.
Zij hebben onlangs het populaire wiskundeboek Mathematics Galore! geschreven, uitgegeven door Oxford University Press.
Dit artikel is gedeeltelijk geïnspireerd door een opmerkelijk debat in het Britse Lagerhuis over het onderwerp kwadratische vergelijkingen. Het verslag van dit debat is te vinden in Hansard, United Kingdom House of Commons, 26 June 2003, Columns 1259-1269, 2003, dat online beschikbaar is op de House of Commons Hansard Debate website.