Math Modeling

Es gibt Funktionen, die stückweise definiert sind. In diesem Abschnitt lernen wir, wie man Funktionen definiert und graphisch darstellt, die im Wesentlichen Sammlungen von diskreten Teilen sind. Beispiele für solche Funktionen sind die Gestaltung des Profils eines Autos, die Berechnung eines Handytarifs oder die Berechnung der Einkommenssteuer. Ihr Steuersatz hängt zum Beispiel von Ihrem Einkommen ab und ist für eine Reihe von Einkommen gleich, wie die folgende Tabelle zeigt:

Eine stückweise Funktion ist eine Funktion, bei der mehr als eine Formel verwendet wird, um die Ausgabe über verschiedene Teile des Bereichs zu definieren.

Wir verwenden stückweise Funktionen, um Situationen zu beschreiben, in denen sich eine Regel oder Beziehung ändert, wenn der Eingabewert bestimmte „Grenzen“ überschreitet. Zum Beispiel treffen wir im Geschäftsleben häufig auf Situationen, in denen die Kosten pro Stück eines bestimmten Artikels reduziert werden, sobald die Anzahl der Bestellungen einen bestimmten Wert überschreitet. Steuerklassen sind ein weiteres praktisches Beispiel für stückweise Funktionen. Stellen Sie sich ein einfaches Steuersystem vor, bei dem Einkommen bis zu 10.000 $ mit 10 % und jedes weitere Einkommen mit 20 % besteuert wird. Die Steuer auf ein Gesamteinkommen, S, wäre 0,1S, wenn S

Auswerten einer stückweise definierten Funktion

Im ersten Beispiel zeigen wir, wie man eine stückweise definierte Funktion auswertet. Beachten Sie, wie wichtig es ist, auf den Bereich zu achten, um zu bestimmen, welcher Ausdruck zur Auswertung der Eingabe verwendet werden soll.

Im folgenden Video zeigen wir, wie man bei einer stückweise definierten Funktion mehrere Werte auswertet.

Im nächsten Beispiel zeigen wir, wie man eine Funktion auswertet, die die Kosten der Datenübertragung für eine Telefongesellschaft modelliert.

Analyse der Lösung

Die Funktion ist in der folgenden Grafik dargestellt. Man sieht, wo die Funktion von einer Konstanten zu einer Linie mit positiver Steigung bei g=2 übergeht. Die Graphen für die verschiedenen Formeln werden auf einer gemeinsamen Achse aufgetragen, wobei darauf geachtet wird, dass jede Formel auf den richtigen Bereich angewendet wird.

C(g) = C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\ 10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Schreiben einer stückweise definierten Funktion

Im letzten Beispiel zeigen wir, wie man eine stückweise definierte Funktion schreibt, die den Preis für eine Museumsführung modelliert.

Analyse der Lösung

Die Funktion ist in Abbildung 21 dargestellt. Der Graph ist eine diagonale Linie von n=0 bis n=10 und danach eine Konstante. In diesem Beispiel stimmen die beiden Formeln am Treffpunkt n=10 überein, aber nicht alle stückweisen Funktionen haben diese Eigenschaft.

Im folgenden Video zeigen wir ein Beispiel für das Schreiben einer stückweise definierten Funktion anhand eines Szenarios.

Grafische stückweise Funktionen

In diesem Abschnitt werden wir stückweise Funktionen grafisch darstellen. Die unten dargestellte Funktion stellt die Kosten für die Datenübertragung bei einer bestimmten Mobilfunkgesellschaft dar. Man kann sehen, wo die Funktion von einer Konstante zu einer Linie mit positiver Steigung bei g=2 übergeht. Bei der Darstellung stückweiser Funktionen ist es wichtig, dass jede Formel auf den richtigen Bereich angewendet wird. \text{ if }{ 0 }<{ g }<{ 2 }\\10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

In diesem Fall ist die Ausgabe 25 für jede Eingabe zwischen 0 und 2. Für Werte gleich oder größer als 2 ist die Ausgabe definiert als 10g+5.

Beispiel

Skizzieren Sie einen Graphen der Funktion.

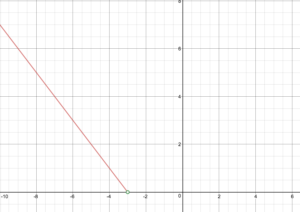
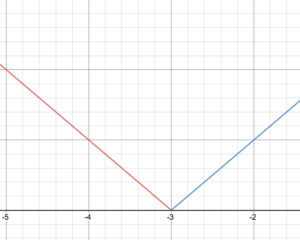
Gegeben die stückweise Definition f(x)=\begin{cases}-x – 3\text{ if }x < -3\ x + 3\text{ if } x \ge -3\end{cases}
Zeichne den Graphen von f.
Bestimme die Domäne und den Bereich der Funktion.

Zeige die Antwort

Zunächst zeichne die Linie f(x) = -x-3, wobei du den Teil ausradierst, in dem x größer als -3 ist. Lege einen offenen Kreis bei (-3,0) an.

Nun lege die Gerade f(x) = x+3 auf den Graphen, beginnend am Punkt (-3,0). Beachte, dass für diesen Teil des Graphen der Punkt (-3,0) eingeschlossen ist, so dass du den offenen Kreis entfernen kannst.

Die beiden Graphen treffen sich im Punkt (-3,0)

Der Bereich dieser Funktion sind alle reellen Zahlen, da (-3,0)nicht als Endpunkt von f(x) = -x-3 eingeschlossen ist, aber er ist als Endpunkt für f(x) = x+3 eingeschlossen.

Der Bereich dieser Funktion beginnt bei f(x)=0 und schließt 0 ein und geht bis ins Unendliche, so dass wir dies als x\ge0

Im nächsten Beispiel werden wir eine stückweise definierte Funktion grafisch darstellen, die die Versandkosten für einen Online-Comic-Händler modelliert.

Beispiel

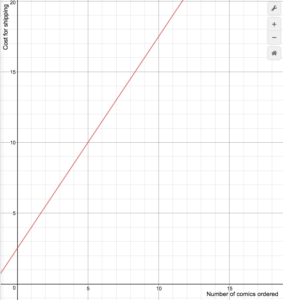
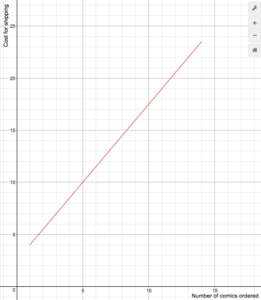
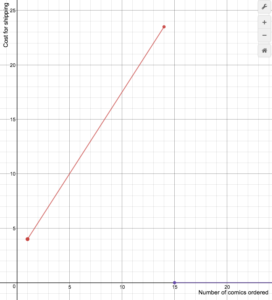
Ein Online-Comic-Händler berechnet die Versandkosten nach der folgenden Formel

S(n)=\begin{cases}1.5n+2.5\text{ if }1\le{n}\le14\0\text{ if }n\ge15\end{cases}

Zeichnen Sie einen Graphen der Kostenfunktion.

Zeige Antwort

Zunächst zeichnen Sie die Linie S(n)=1.5n+2.5. Wir können Transformationen verwenden: dies ist eine vertikale Streckung der Identität um den Faktor 1,5 und eine vertikale Verschiebung um 2,5.

S(n)=1,5n+2.5

Nun können wir die Teile des Graphen eliminieren, die nicht in der Domäne liegen, die auf 1\le{n}\le14

S(n) = 1.5n+2.5 für 1<=n<=14

Zuletzt fügen wir die konstante Funktion S(n)=0 für Eingaben größer oder gleich 15 hinzu. Setzen Sie geschlossene Punkte an die Enden des Graphen, um die Einbeziehung der Endpunkte anzuzeigen.

Im folgenden Video zeigen wir, wie man eine stückweise definierte Funktion, die über beide Bereiche linear ist, grafisch darstellt.

Zusammenfassung

• Eine stückweise Funktion ist eine Funktion, bei der mehr als eine Formel verwendet wird, um die Ausgabe über verschiedene Teile der Domäne zu definieren.
• Die Auswertung einer stückweisen Funktion bedeutet, dass Sie genau auf den richtigen Ausdruck achten müssen, der für die gegebene Eingabe verwendet wird

Um stückweise Funktionen grafisch darzustellen, ermitteln Sie zunächst, wo die Domäne geteilt ist. Graphen Sie die Funktionen auf der Domäne mit Hilfe von Hilfsmitteln wie Plotting Points oder Transformationen. Achten Sie darauf, offene oder geschlossene Kreise an den Endpunkten jeder Domäne zu verwenden, je nachdem, ob der Endpunkt eingeschlossen ist.