AMS :: 特集コラム ::: なぜ双子の素数が多いのか？

一つの重要な疑問は、整数の中で素数はどのように分布しているかということである。その答えは、ごく簡単に言えば、ある基本的な統計があれば、かなりランダムに分布する…

Bill Casselman
University of British Columbia, Vancouver, カナダ
Eメール Bill Casselman

友人にメールする

この記事を印刷する

Introduction
How many primes do we expect?
Heuristic reasoning about twin primes
Dickson’s conjecture
最近起こったこと

Introduction

数年前に、$p$, $q$で$q=p+2$の素数対が無数にあると推測されたことがあります。この問題については、最近（そして有名な）進展がありました。ここでは、最近の進展についてはほとんど触れず、その代わりに、このような組について、わかっていることよりもむしろ、期待されることについて述べることにする。

How many primes do we expect?

A prime number is a positive integer that has no divisors except itself and $1$. 定義は簡単ですが、素数の意味を調べ始めると、素数が多くの微妙な振る舞いをすることに気づきます。重要な問題の一つは、素数は整数の中でどのように分布しているのか、ということである。その答えは、ごく簡単に言えば、ある基本的な統計量からすれば、むしろランダムである。これはどういうことかというと、

さて、ここに$400$までのすべての素数を描いた正方形の配列があります：

この配列には、いくつかのパターンがあります。あなたが認識するそれらのほとんどは、ディスプレイの何らかのアーチファクトに起因するものです。たとえば、1つおきの列は基本的に空で、これは偶数の素数が $2$ だけだからです。また、5列目も本質的に空である。さらに興味深いのは、双子の素数のペア（中には$59$と$61$のように2列に分かれていてあまり見えないものもある）と、表示される最後の桁に関連するいくつかのパターンである。これらは、ローカルパターンと呼ばれるものである。 693>

素数を非常に効率的に生成する方法には多くの努力が払われてきましたが、最近では非常に簡単なプログラムでも、大きな素数のリストを作るのにわずかな時間しかかからなくなりました。最も実りあるプログラムの1つは、素数の大きなリストを作り、これを使って素数の個数$ginle n$である関数$pi(n)$を計算します。

これが使えることの1つは、素数の頻度を大まかに把握できることです。 135$ 個の素数が $$:

の範囲にあります。

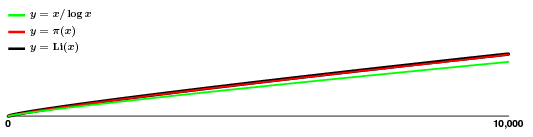
この近似はとても良さそうですね。つまり、$pi(x)$が少し跳ね回っていて、一見あまりパターンがないように見えても、かなり良い推定値が得られたので、少なくとも平均的には素数がどのように成長するかがよくわかったことになります。

しかしながら、この見かけの滑らかさはごまかしであることに注意しなければなりません。

Comments?

Heuristic reasoning about twin primes

Twin primes are a pair $p$, $p+2$ which are both primes.これは、双子の素数である。例えば、上のプロットの1つから、双子の素数 $$ , , , , $$

などが見えます。その数は無限であると推測されているが、多くの経験的証拠があり、まだ証明されていない。

おそらく最も強い証拠は、双子素数 $le x$ の数 $pi_{2}(x)$ を非常によく近似する公式であろう。この公式の起源はよくわかりませんが、1923年のG. H. HardyとJ. E. Littlewood（彼ら自身も双子素数のペアです）の論文に初めて登場します。この論文には似たような公式がいくつか含まれているが、すべて同じ方法に基づいており、彼らはそれ以前に多くの問題を攻略していたのである。これが彼らの円環法である。彼らの$pi_{2}(x)$の公式の導出は、厳密なものでは全くないが、非常に説得力のあるものである。アンドリュー・グランビルの論文の付録に、これについての簡潔な説明がある

しかし、第二次世界大戦直後、チャーウェル卿（フレデリック・リンデマン）は、より初歩的な確率的導出（それでも厳密とはいえない）を提案した。これがE・M・ライトとの共同研究につながり、最終的には死後の共同出版に至った。このことは、ハーディとライトの有名なテキストの22.20節で説明されている。また、Granvilleの論文の付録（2.5節）にも、これのもう少し初歩的なものがある。 693>

もっともらしい推論の出発点は、$x$以下の素数の数である$pi(x)$の我々の推定値である。この導出の基本的な考え方は、素数はかなりの程度、ランダムに分布しているということである。 x$の近傍では、素数の密度は約1/log x$であることが分かっている。もし、素数がランダムに分布しているならば、$x$近傍の任意の2つの数が素数である確率は、局所確率の積だけで、$1/log^{2} x$となるはずである。 n > 2$ なら $n$ と $n+1$ がともに素数である確率は $0$ であり、$p$ が素数であることは $p+2$ である確率を高めるように見えるから、これは確かに思わせぶりな推論である。 x$の近傍では、他の小さな素数で割り切れる可能性もあるため、同様の考慮が必要である。 q$を任意の素数とすると、$q$で割り切れない整数をランダムに選ぶ確率は$1-1/q$である。したがって、$q$で割り切れない2つを選ぶ確率は、$(1 – 1/q)^{2}$ の積となる。 p$と$p+2$がともに素数だとすると、$p$と$p+2$のどちらも$q$で割り切れない。 q = 2$のとき、これは1/2$の確率で起こる。 qが2$のとき、$pが$p \notequiv 0$と$p \notequiv -2$ modulo $q$である確率は$(1 – 2/q)$である。中国の余弦定理により、2つの素数で割り切れることは独立な事象である。したがって、$x$ が大きく、$Q$ が比較的小さいとき、$x$ の近くの数$m$ と$n$ の組が$Q$ までのどの素数の倍数にもならない確率は$$ { 1over 2} \cdot ¢prod_{q¢le Q} である。 { (1 – 1/q)^{2} } \Γ, . $$

Let $Gamma_{Q}$ be ratio of this to $prod_{q \le Q}(1 – 2/q)$: $$ \Gamma_{Q} = { 1over 2} \cdot \prod_{q \le Q}.この比は、Γ(Q)とQ(Q)の比とする。 { (1 – 1/q)^{2} \ʕ-̫͡-ʔʔ ここで、$$ { 1 – 2/q \over (1-1/q)^{2}が得られる。 } = { (1 – 1/q)^{2} – 1/q^{2} \(1 – 1/q)^{2}。 } = 1 – { 1 \over (q -1)^{2}. } \, … $$ 標準的な基準では、和$sum 1/(q-1)^{2}$ が収束すれば、この積は収束すると断言される。しかし、積分テストでは、$sum 1/n^{2}$ が収束することがわかるので、収束します。よって、この積は、実際には、$Q \rightarrow \infty$ として、数$Pi_{infty}$ に収束する。その逆数を$C_{2}$とする。グランビルの論文の2.5節によると、この時点で双子素数$le x$の数$pi_{2}(x)$は$$ \Pi_{2}(x) = C_{2}で近似されることが直感的に分かるはずです。 \int_{2}^{infty} { dx ╱log^{2} x }. \．$

Hardy and Wrightのテキストでは、より丁寧な解析が行われており、直感的な飛躍がもう少し明確になる。

ここでの定数の値は、昔、J・W・Wrenchが約1ドルと計算したものである。320323631693914785562422002911155686525 \ldots $. ここで、$$の範囲で$pi_{2}(x)$のいくつかの値と公式を比較してみましょう： $$ \matrix{ n & 10,000 & 20,000 & 30,000 & 40,000 & 50,000 ♪cr \pi_{2}(n) & 205phantom{.0} & 342 \phantom{.0} & 467 \phantom{.0} & 591 \phantom{.0｝ & 705 \phantom{.0} & & 357.7 & 486.7 & 607.4 & 722.5 \cr } ⑭Pi_{2}(x) & 214.2 & 357.7 & 486.7 & 607.4 & 722.5 $$ $$ \matrix{ n & 6万 & 7万 & 8万 & 9万 & 10万 & 905 ㎤㎤㎤㎤ (n) & 1007 ㎤㎤㎤㎤ & 1116 ♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪ & 1224phantom{.0} \⑭Pi_{2}(x) & 833.3 & 940.9 & 1045.7 & 1148.2 & 1248.7 \cr } ⑯Pi_{2}(x) & 1045.7 & 1148.2 & 1248.7 $$

Comments?

Dickson’s conjecture

Twin primes is a special case of something far more general.これは、双子の素数は、より一般的なものの特殊な例です。素数である $p$, $p+4$ や $p$, $p+6$ のペアは無限にあるのだろうか？あるいは、$p$, $p+10$のペアは無限にあるのだろうか？ p$と$p+10$の場合は、確かに上の画像にあるように、そのようなペアが簡単に見えることが示唆されています。では、3つ組の場合はどうでしょうか。 a_{1}$, $a_{2}$, $ldots$ , $a_{k}$が整数の配列を構成しているとします。 n+a_{1}$, $n+a_{2}$, $ldots$ , $n+a_{k}$はすべて素数である集合が無限に存在すると考えてよいでしょうか？

少し注意しなければならないことがあります。 p$, $p+1$ の形（過去 $p = 2$ ）の素数対は存在しない、なぜならこの二つの数のうち一つは $2$ で割り切れるものでなければならないからである。同様に、$p = 3$を過ぎると、$p$, $p+2$, $p+4$の形の素数三重奏は存在しない。なぜなら、これらのうちの1つは$3$で割り切れなければならないからだ。 p+4$ という数は、$p+1$ が $3$ で割り切れるときだけ、$3$ で割り切れる。したがって、$3$は$p$, $p+2$, $p+4$のいずれかを割り切れるのは、$p$, $p+1$, $p+2$のいずれかを割り切れる場合のみである。しかし、最後のトリプルは明らかに$3$モジュロのすべての数をカバーしているので、これは確実に起こる。

一般に、$p$がすべての配列$n+a_{i}$ ($i = 1$, $ldots$, $k$)を常に少なくとも一つ分割していれば、配列$(a_{i})$にとって障害であると言われる。このことは、数$a_{i}が \; {rm mod} \Ъ, p$ が $Z/p$ をすべて埋めてしまう。

これは $p > k$ なら絶対に起こりえないので、ある $p$ が $(a_{i})$ を妨害しているかを調べるには、すべての $p \le k$ に対して $a_{i}$ が $Z/p$ をカバーしているかを調べればいいのである。

例えば、$(1,3,7,9)$は、簡単に調べられるように$2$も$3$も障害にならないので、許容配列と呼ぶことにする。このパターンに当てはまるいくつかの素数列は、上の図の1つに見ることができます。他の例としては、(a) 任意の $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$ がある。

任意の大きさの許容集合が存在する。実際:

定理。 a_{1}$から$a_{k}$が任意の明瞭な素数$> k$の集合であれば、それらは許容集合を構成する。

これはなぜか。 p$が$p> k$となる任意の素数であれば、妨害になり得ないことは既に見たとおりである。しかし、$pがk$の場合は、$a_{i}$のどれにも割り込めず、$p$のモジュロで$0$と合同になるものはない。したがって、$a_{i}$は$Z/p$を埋め尽くさない。

L・E・ディクソンが最初に立てた予想の特殊例として、$(a_{i})$に対する素数の障害がない場合、$(n +a_{i})$の形の素数列が無限に存在する、というのがある。