学習目標
このセクションの終わりまでに、次のことができるようになります:
- Explain the law of energy.
- 多くのエネルギーの形態のいくつかを記述すること。
- エネルギー変換プロセスの効率を、たとえば熱エネルギーに変換されるのではなく、有用なエネルギーまたは仕事として残る割合と定義する。
Law of Conservation of Energy
エネルギーは、これまで述べたように保存されているので、自然界の最も重要な物理量の一つになっている。 エネルギー保存の法則は次のように述べることができる:
全エネルギーはいかなる過程においても一定である。 形が変わったり、ある系から別の系に移ったりしても、合計は同じままである。
私たちは、エネルギーのいくつかの形と、それがある系から別の系に移されるいくつかの方法について調べました。 この探索により、機械的エネルギー (KE + PE) と非保存力によって行われる仕事を通じて伝達されるエネルギー (Wnc) という 2 つの主要なタイプのエネルギーを定義することに成功しました。
機械的エネルギー以外のエネルギー
この時点で、他のすべてのエネルギー形態は、他のエネルギー(OE)という1つのグループにまとめて扱われることになります。 そして、エネルギー保存を方程式形式で、KEi + PEi + Wnc +OEi = KEf + PEf + OEfと述べることができる。
すべての種類のエネルギーと仕事は、エネルギー保存のこの非常に一般的な声明に含めることができる。 運動エネルギーはKE、保存力によってなされる仕事はPE、非保存力によってなされる仕事はWnc、その他すべてのエネルギーはOEとして含まれる。 この式は、これまでのすべての例に当てはまります。これらの状況では、OEは一定なので、引き算され、直接考慮されることはありませんでした。 エネルギー保存原理の有用性
エネルギーが保存され、多くの形態を持っているという事実が、それを非常に重要なものにしています。 エネルギーはすべてのプロセスに関与しているため、多くの文脈で議論されていることがわかります。 また、多くの状況はエネルギーの観点から最もよく理解され、問題はエネルギーを考慮することで最も簡単に概念化され解決されることが多いことも明らかになります。
OEはいつ役割を果たすのでしょうか。 1つの例は、人が食事をするときに起こります。 食べ物は酸化され、二酸化炭素、水、およびエネルギーが放出される。 この化学エネルギーの一部は、人が動くと運動エネルギーに、人が高度を変えると位置エネルギーに、そして熱エネルギー(OEの別の形態)に変換されます。
エネルギーの多くの形態の一部
エネルギーの他の形態のいくつかとは何ですか? まだ議論されていないエネルギーの形をいくつも挙げることができるでしょう。 これらの多くは後の章で取り上げますが、ここではそのいくつかを詳しく説明しましょう。 電気エネルギーは一般的な形態で、他の多くの形態に変換され、実用的な場面で広く使われています。 ガソリンや食品などの燃料は、化学エネルギーを持ち、酸化することでシステムに伝達することができる。 また、化学燃料は、電池のように電気エネルギーを生み出すこともできます。 電池は光を生み出すことができ、これは非常に純粋なエネルギーである。 地球上のほとんどのエネルギー源は、実は太陽から受け取るエネルギーが蓄積されたものなのです。 可視光線、赤外線、紫外線などを含む放射エネルギー、または電磁放射と呼ぶことがあります。 核エネルギーは、測定可能な量の質量をエネルギーに変換するプロセスから生まれます。 核エネルギーは、太陽光のエネルギー、発電所の電気エネルギー、兵器の熱伝導や爆風などのエネルギーに変換される。 すべての物体の中の原子や分子は、ランダムに運動している。 このランダムな運動による内部の力学的エネルギーは、物体の温度と関係があるため、熱エネルギーと呼ばれています。 これらのエネルギーや他のすべてのエネルギーは互いに変換することができ、仕事をすることができる。
表1は、さまざまな物体やさまざまな現象で貯蔵、使用、または放出されるエネルギー量を示している。
エネルギーに関する問題解決戦略
エネルギーを扱うときはいつでも、以下の問題解決戦略が役に立つと思います。 このストラテジーはエネルギーの概念を整理し、強化するのに役立ちます。 実際、この章で紹介する例題でも使われています。 物理的な原理、既知と未知を識別すること、単位を確認することなど、先に紹介したおなじみの一般的な問題解決方法は、ここでも引き続き関連します。
ステップ1. 対象となるシステムを決定し、どのような情報が与えられ、どのような量が計算されるかを特定します。 スケッチが役に立ちます。
ステップ2. 関係するすべての力を調べ、力によって行われる仕事から位置エネルギーを知っているか、与えられているかを判断する。 その後、ステップ3またはステップ4を使用します。
ステップ3. 問題に入る力の位置エネルギーがわかっていれば、力はすべて保存的であり、位置エネルギーと運動エネルギーの観点から単純に力学的エネルギー保存を適用することができる。 エネルギー保存を表す式は、KEi+PEi=KEf+PEfです。
ステップ4. 力の一部しか位置エネルギーを知らない場合、おそらく非保存的で位置エネルギーを持たないものがあるため、または力と仕事の観点から簡単に扱えない他のエネルギーがある場合、最も一般的な形のエネルギー保存則を使用しなければなりません。
KEi + PEi + Wnc + OEi = KEf + PEf +OEf.
ほとんどの問題で、一つまたは複数の項はゼロで解を単純化することができるのです。 保存力によって行われる仕事であるWcは計算しないでください。それはすでにPEの項に組み込まれています。 あなたはすでに(ステップ2で)関係する仕事とエネルギーの種類を特定しました。 未知数を解く前に、可能な限り項を削除し、代数を簡略化する。 例えば、初期点または最終点でh=0を選び、そこでPEgがゼロになるようにする。 その後、通常の方法で未知数を解く。
ステップ6. 答えが妥当かどうか確認する。 問題を解いたら、仕事とエネルギーの形を見直し、エネルギー保存式の設定が正しいかどうかを確認します。 例えば、摩擦に対して行われる仕事は負でなければならない、丘の底の位置エネルギーは頂上の位置エネルギーより小さくなければならない、などです。 また、得られた数値が妥当かどうかもチェックしましょう。 例えば、高さ3mのスロープを惰性で下るスケートボーダーの最終速度は、時速20kmは妥当だが、時速80kmにはならない。
エネルギーの変換

図1. 太陽エネルギーは太陽電池によって電気エネルギーに変換され、このソーラーパワー航空機のモーターを動かすのに使われる。 (credit: NASA)
ある形から他の形へのエネルギーの変換は常に行われています。 食べ物の化学エネルギーは代謝によって熱エネルギーに変換され、光エネルギーは光合成によって化学エネルギーに変換される。 もっと大きな例では、石炭に含まれる化学エネルギーは、燃焼することで熱エネルギーに変換され、ボイラーで水を蒸気に変えています。 この蒸気の熱エネルギーを機械エネルギーに変換してタービンを回し、タービンを発電機につないで電気エネルギーを発生させる。 (いずれの例も、最初のエネルギーがすべて変換されるわけではありません。 この重要な点については、このセクションで後述します)
エネルギー変換のもう一つの例は、太陽電池で起こります。 太陽電池に降り注ぐ太陽光(図1参照)から電気が発生し、その電気でモーターを動かすことができる。 エネルギーは、太陽エネルギーという一次エネルギー源から電気エネルギーに、そして機械エネルギーに変換される。 さまざまな物体や現象のエネルギー
で解放されたエネルギー
効率
エネルギー変換過程でエネルギーを保存しても、有効エネルギーや仕事の出力は入力エネルギーより小さくなってしまう。 エネルギー変換過程の効率Effは次のように定義される
displaystyle}(Eff)=Aufrac{text{useful energy or work output}{text{total energy input}}=Aufrac{W_{text}out}{E_{text}in}}
表2に機械装置と人間活動の効率の一部を列記した。 例えば石炭火力発電所では、石炭中の化学エネルギーの約40%が有用な電気エネルギーになる。 残りの60%は熱エネルギーなど他の(おそらくあまり有用でない)エネルギー形態に変換され、燃焼ガスや冷却塔を通じて環境に放出される
| 表2。 人体と機械装置の効率 | |
|---|---|
| 活動/装置 | 効率(%) |
| サイクリングと登山 | 20 |
| 水泳。 水面 | 2 |
| 遊泳。 水中 | 4 |
| ショベル | 3 |
| 重量上げ | 9 |
| スチームエンジン | 17 |
| ガソリンエンジン | 30 |
| ディーゼルエンジン | 35 |
| 原発 | 35 |
| 石炭発電所 | 42 |
| 電気モーター | 98 |
| 小型蛍光灯 | 20 |
| LED30 | |
| ガスヒーター(住宅用) | 90 |
| 太陽電池 | 10 |
PhET Explorations.Phet(フェット・エクスプローラ Masses and Springs
リアルな質量とバネの実験室です。 バネに質量をぶら下げ、バネの硬さや減衰を調整します。 時間を遅くすることもできます。 実験室をいろいろな惑星に移動させることができます。
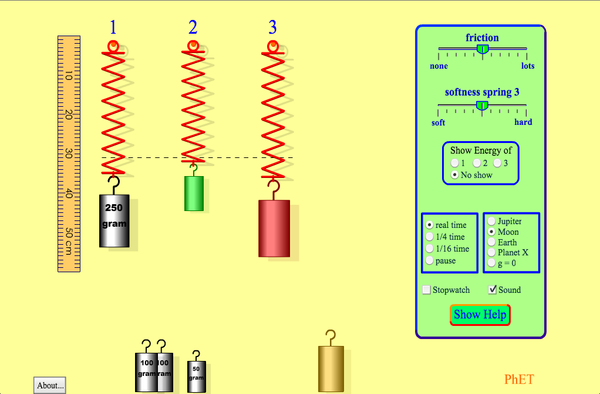
Click to run the simulation.
Section Summary
- The law of conservation of energy states that the total energy is constant in any process.The law of conservation of energyは、どのようなプロセスにおいても総エネルギーが一定であることを述べています。
- エネルギーのすべての形態を考慮する場合、エネルギー保存は方程式形式で KEi + PEi + Wnc + OEi = KEf + PEf + OEf と書き、OE は機械エネルギー以外のすべてのエネルギー形態である。
- エネルギーはしばしば仕事をするために利用されるが、システムのすべてのエネルギーを仕事に変換することは不可能である。
- 機械や人間の効率Effは、Woutを有用な仕事の出力、Einを消費するエネルギーとすると、 \text{Eff}={W}_{text{out}}{E}_{text{in}}} と定義される。 摩擦が無視できない自動車が、静止状態から加速して坂を下り、少し走ったところでガソリンが尽きた。 運転手は車を坂の下まで惰性で走らせ、小高い丘を登って越える。 そして、その坂を惰性で下ってガソリンスタンドに入り、そこでブレーキを踏んで停車し、ガソリンを満タンにした。 車が持っているエネルギーと、そのエネルギーがこの一連の出来事でどのように変化し、伝達されるかを明らかにしなさい。 (図2参照)

図2.
- 無視できない摩擦を経験している車が惰性で坂を下り、小山を越え、再び坂を下り、ガソリンスタンドで停止する。 これらの各位置には下向きの矢印が付けられている。
- 選手が槍を拾い上げた時点から始まり、投げた後に槍が地面に突き刺さった時点までの、槍のエネルギー移動と変換を説明せよ。
- 効率が1未満の機器はエネルギー保存則に違反するか。 説明せよ。
- エネルギーの形を4種類挙げよ。 それぞれの形態から別の形態への変換の例を1つ挙げよ。
- 自転車に乗るときに起こるエネルギー変換を挙げよ。
問題 & 練習問題
- 表1の値を使って、旧式のテレビ管のビーム中の電子1個が運ぶエネルギーで壊せるDNA分子の数は何個だろうか。 (この電子はそれ自身は危険ではないが、危険なX線を発生させる)。 後世のブラウン管テレビは、X線が外に出て視聴者に照射される前に吸収するシールドを備えている)
- エネルギーの考察を用い、空気抵抗を無視できると仮定して、水上20.0mの橋から初速15.0mの石を投げた場合、その石は水面から離れることを示せ。4138>
- もし核融合爆弾のエネルギーが世界のエネルギー需要を満たすために使われるとしたら、9メガトン級のものは1年分のエネルギー供給にいくつ必要でしょうか(表1のデータを使用)。 核爆弾は何千個もあり、そのエネルギーは自然の地熱エネルギーと同じように地下爆発に閉じ込められ、電気に変換することができるのです。 核融合は表1からわかるように、比較的クリーンでほぼ無限のエネルギー供給が可能であろう。 これを説明するために、現在の世界のエネルギー需要を、海洋の100万分の1の水素核融合エネルギーで何年供給できるか計算してみよう。 (b) この時間は、安定した経済システムの継続期間など、歴史的に重要な出来事と比較してどうだろうか。
Glossary
エネルギー保存則:あらゆるプロセスにおいて総エネルギーが一定であるという一般法則;エネルギーはあるシステムから別のシステムに形を変えたり移動したりしても、合計は同じ
electrical energy: 電荷の流れによって運ばれるエネルギー
化学エネルギー:化学反応で放出することができる原子と分子の間の結合に格納されている物質中のエネルギー
放射エネルギー:電磁波によって運ばれるエネルギー
核エネルギー:電気エネルギー。 2つの軽い原子核の融合や重い原子核の核分裂など、原子核内の変化によって放出されるエネルギー
熱エネルギー:その原子や分子のランダムな運動による物体内のエネルギーで、物体の温度を説明する
効率。 548>
Selected Solutions to Problems & Exercises
1. 4×104分子
2. ΔPEgとΔKEを等化すると、v=sqrt{2gh+v_0^2}=Cheekt(9.80m/s}^2left)+Phaseleft(20.0 text/ m}/Right)^2}=24.0.8text{ m/s}}
4. (a) 25 × 106 years; (b) This is much, much longer than human time scales.
- Representative values ↵