Half Adder and Full Adder Circuit
Half Adder and Full Adder Circuitを真理値表とともに説明する。 また、半加算器回路を用いた全加算器の設計も紹介します。 1ビットFull Adder回路とFull Adderを用いた多ビット加算回路も示す。
このテーマに入る前に、ブール論理と論理ゲートについて知っておくことが非常に重要です。
TAKE A LOOK : BOOLEAN LOGIC
TAKE A LOOK : LOGIC GATES
TAKE A LOOK : FLIP FLOPS
加算器とは
2 進数の加算に使われる計算機の一種である加算器は、2 進数の加算に使用されている計算機のことです。 電卓といってもボタンがあるようなものではなく、他の多くの回路と統合して幅広い用途に使えるような回路です。 加算器には2種類あり、
- 半加算器
- 全加算器
半加算器
論理ゲートにより単純な加算ができる回路を設計することが可能です。
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
これらの組み合わせは1ビットとしては最も少ないものである。 しかし、1+1の結果は10です。 この問題はEXORゲートで解決できますが、出力にこだわるなら、和の結果を2ビット出力に書き換える必要があります。
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
ここで「10」の「1」が繰り上げ出力となります。 その結果を真理値表で表すと次のようになる。 SUM」が通常の出力で、「CARRY」がキャリーアウトである。
INPUTS OUTPUTS
A B SUM CARRY
0 0 0
0 1 1 0
1 0 1
1 1 0
この式から、’1’は’1’である。 この1ビット加算器は、出力「SUM」用のEXORゲートとキャリー用のANDゲートを使えば、簡単に実装できることがわかります。
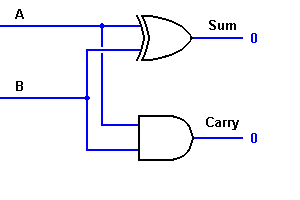
複雑な加算を行う場合、8ビットバイトを2つ加算しなければならないことがあります。
フルアド
このタイプの加算器は、ハーフアドより実装が少し難しいです。 半加算器と全加算器の主な違いは、全加算器は3つの入力と2つの出力を持っていることです。 最初の2つの入力はAとBで、3番目の入力はCINと呼ばれる入力キャリーである。 フルアドのロジックが設計されると、8個のフルアドを連結してバイト単位の加算器を作り、キャリービットを1個の加算器から次の加算器にカスケード接続することができるようになる。
入力 出力
a b cin cout s
0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 1
1 0 1 0
1 1 0 1 0
1 1 1 1
上記の真理値から、「1.の表をご覧ください。 を実装することができます。 出力Sは、入力Aと、BとCINを入力とする半加算器SUM出力との間のEXORであることがわかる。 また、COUTは3つの入力のうち2つがHIGHのときのみ真になることにも注意しなければなりません。
このように、2つの半加算回路を使えば、全加算回路を実装することができます。 最初の半加算器は、AとBを加算して部分和を生成するために使用されます。 2番目の半加算器は、CINを最初の半加算器のSumに加算して、最終的なS出力を得るために使用できます。 半加算器ロジックのいずれかがキャリーを生成する場合、キャリーが出力されます。 したがって、COUTは半加算器のキャリー出力のOR関数となります。
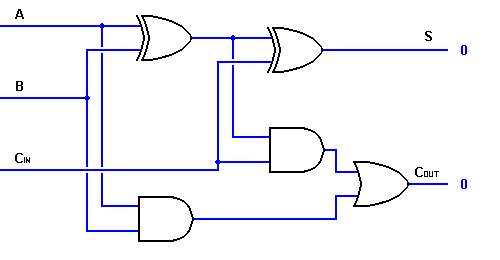
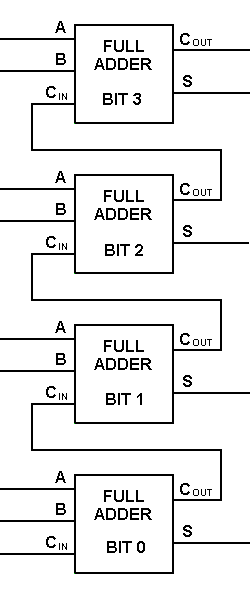
上記のフルアドロジックでは、より大きな論理図の実装が可能ですが、操作を表すにはより単純な記号が使われることがほとんどです。
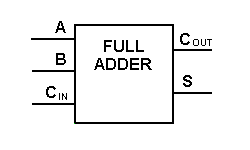
このような記号で、2ビットを加算して、次の低次の桁からキャリーを取って、次の高次の桁にキャリーを送ることができます。 コンピュータでは、多ビット演算の場合、各ビットをフルアダーで表現し、同時に加算する必要があります。 したがって、2つの8ビット数を加算するには、4ビットブロックを2つカスケード接続することで形成できる8個の全加算器が必要となる。 以下は、2つの4ビット数の加算です。