Prerequisite – Measures of Distance in Data Mining
データマイニングでは、類似度測定はデータセット内の、データオブジェクトの特徴を表す次元との距離を指します。 この距離が小さいと類似度が高く、距離が大きいと類似度が低くなります。
一般的な類似度測定には、-
- Euclidean Distance(ユークリッド距離)などがあります。
- マンハッタン距離.
- ジャカード類似度.
- ミンコスキー距離.
- コサイン類似度.
コサイン類似度は、データオブジェクトがそのサイズにかかわらず、どれだけ似ているかの決定に役立つ指標である。 Python でコサイン類似度を使用して 2 つの文の間の類似性を測定することができます。 コサイン類似度では、データセットのデータオブジェクトはベクトルとして扱われます。 2つのベクトル間のコサイン類似度を求める式は –
Cos(x, y) = x . y / ||x|| * ||y||
ここで、
- x . y = ベクトル ‘x’ と ‘y’ の積(点)である。
- ||x|| と ||y|| = 2つのベクトル ‘x’ と ‘y’ の長さ.
- ||x| * ||y|| = 2つのベクトル ‘x’ と ‘y’ の交差積 .
例題.
2 つのベクトル ‘x’ と ‘y’ の間の類似性をコサイン類似度を使用して求める例を考えてみましょう。
‘x’ ベクトルは値、x = { 3, 2, 0, 5 }
‘y’ ベクトルは値、y = { 1, 0, 0, 0 }
コサイン類似度の計算式は、: Cos(x, y) = x . y / ||x| * ||y|
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1∴ Cos(x, y) = 3 / (6.16 * 1) = 0.49
二つのベクトル ‘x’ と ‘y’ の非類似度は、-
∴ Dis(x, y) = 1 - Cos(x, y) = 1 - 0.49 = 0.51
- 二つのベクトルの余弦類似度は、 ‘θ’ で測られます。
- θ = 0°の場合、’x’ と ‘y’ のベクトルは重なり、したがってそれらは似ていることを証明する。
- θ = 90°の場合、 ‘x’ と ‘y’ のベクトルは非類似である。
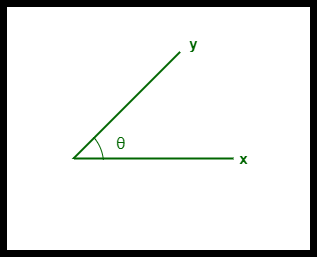
Cosine Similarity between two vectors
Avantages :
- cosine similarity is beneficial because two similar data objects are far apart by the Euclidean distance because the size, they can still have the smaller angle between them.The two collows are similarization.
- 多次元空間にプロットすると、余弦類似度は大きさではなく、データオブジェクトの方向(角度)を捉えることができる。
DBMS実践編 タグ :