GENERAL CHEMISTRY TOPICS
Energy: 基礎的な概念
エネルギーの形態。 運動エネルギーと位置エネルギー、仕事とエネルギー、熱と温度、静電位置エネルギー
エネルギー：運動エネルギーと位置エネルギー
エネルギーの概念は物理科学の基本である。 ここでは、エネルギーに関するいくつかの第一原理を示し、化学にとって特に重要なエネルギーの形を紹介することを目的としています。 まず、観測の対象となる宇宙の一部を「系」と定義することが非常に有効である。 システムは、物体または物体の集まりで構成され、現実または想像上の境界によって、宇宙の他の部分（私たちは周囲と呼んでいる）と区別されます。
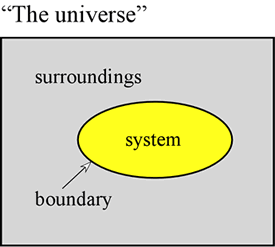
金属の円筒のような一定の容積を持つ気体のサンプルはシステムの一例で、気体の一般的な性質を研究する際に関連するものである。 さらに、風船の中の気体や、ピストン付きシリンダーの中の燃焼混合物もその一例である。 これらの場合、系は物理的な、しかし移動可能な境界によって囲まれており、系の体積は固定されていない。 さらに、試験管やビーカーの中で化学反応を起こしている溶液中の混合物の例もよく検討される。 ここで紹介した用語は、エネルギーが化学系でどのように現れるかを研究する際に特に重要であり、それは主に熱力学の見出しに該当する。
一般化学では、関連すると考えられる系は通常静止状態にあり、重力効果は無視される。 多くの場合、化学反応が起こる系に最も関心があり、系の化学組成は時間と共に変化する。 しかし、当面は、振り子やビリヤードのボールが転がり、衝突するような力学系を使用して、エネルギーに関する一般原理を理解するために、より広い視点を採用することにしよう。 運動エネルギーとは、物質が運動するときのエネルギーである。 物理学では、運動エネルギー (KE) の正確な数学的定義を提供しており、次の式 (左下) で示される。
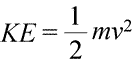ここで、オブジェクトの運動エネルギーは、オブジェクトの質量 (m) とその速度 (v) の二乗の積として表され、さらに定数 ½ が掛けられたものである。 システムが複数の物体から構成されている場合、全運動エネルギーは個々の物体の運動エネルギーの和として表現される。 エネルギーのSI単位はジュール（J）で、次のように定義される：
1 J = 1 kg-m-s-2
位置エネルギーは、通常何らかの形で運動エネルギーに変換できる系のエネルギーで、何らかの方法で仕事という量（以下でさらに説明）を生み出すことができる。 位置エネルギーのわかりやすい例として、建物の縁にあるレンガがある。 このレンガは、その高さ、つまり重力場に対する位置によって、ある程度の位置エネルギーを持っています。 このレンガを少し動かして棚から落とすと、レンガは自然に重力位置エネルギーの低い方向に移動し、その際に運動エネルギーを獲得する。 また、電池の電気的位置エネルギー（電圧で表される）もその一例である。 電池の両端子を針金と電球で結んで回路を作ると、両者の電位差によって針金の中の電子が動き（運動エネルギー）、熱と光が発生する。
エネルギーに関する重要な一般原則は、エネルギーは作り出すことも破壊することもできないということである。 これはエネルギー保存の法則として知られている。 定量的には、落下するレンガや時計の振り子のような系では、運動エネルギーと位置エネルギーの和は一定であることを意味します。 実際の振り子では、摩擦によってエネルギーの一部が失われ、振り子が揺れ続ける（時計が動く）ためには、わずかなエネルギーが振り子に加えられる必要があるため、これはやや抽象的な表現となる。 しかし、そのような「失われた」エネルギー（実際には周囲の空気分子の熱エネルギーの増加として現れる）を注意深く実験的に測定して考慮すると、確かにエネルギーは常に保存されていることが分かる。 もう一つの注意点は、質量とエネルギーの基本的な等価性を表すアインシュタインの有名な方程式E = mc2に集約されている。 エネルギー保存則をより一般化したものが、質量エネルギー保存則と呼ばれるもので、この等価性を説明するものである。 一般化学に戻ると、このような物質とエネルギーの相互変換は一般にその領域ではなく、核反応と放射能の研究は核物理学に包含される。
化学変化が熱の生成を伴う化学反応を考える場合、疑問が生じる。 この場合、エネルギー保存はどうなるのだろうか。 その答えは、化学ポテンシャルエネルギー（または単に化学ポテンシャル）と呼ぶことのできるポテンシャルエネルギーが、反応物の分子組成に存在すると考えることができるからである。 この位置エネルギーは、熱というエネルギーに変換されるが、熱の発生を定義し測定することができれば、存在する正味のエネルギー量は一定であることが分かる。 化学的位置エネルギーとして理解できる日常的な例は、ガソリンエンジンである。ガソリンと酸素の混合物は、潜在的なエネルギーを持っているのだ。 このガソリンと酸素の混合物の潜伏エネルギーが消費されて、自動車の運動エネルギーが生まれるのである。 さらに、力学の法則は、仕事-エネルギーの定理によってエネルギーと結びつけることができる。 サッカーボールを蹴るなどして、力を加えることによって物体の運動エネルギーを増大させることができるという考えを示しています。 この考え方を一般化したものが仕事エネルギーの定理で、おおよそ次のようになる。 物体の持つエネルギーの変化は、物体に作用する力の大きさに、その力が作用する距離を掛けたものに等しい。
仕事の結果として系に生じるエネルギー変化は、系から見て正にも負にもなりうる。 仕事はシステムによって行われることもあれば、システムが周囲から仕事を受けることもある。 仕事がシステムによって行われる場合、システムはエネルギーを周囲に失います。 もしシステムが仕事をすれば、システムのエネルギーは増加する。 例えば、ピストンが動くシリンダー内で火花が混合気を爆発させると、システムが急速に膨張し、その膨張が周囲にあるロッドの動きと機械的に結合される場合、シリンダーのシステムは周囲に仕事をし、そうすることでエネルギーを失う。 これはもちろん、内燃機関が化学的な位置エネルギーを、自動車が動くときの運動エネルギーに変換する仕組みの一部である。
仕事とエネルギーの定理の1つの意味は、単位に関するもので、つまり仕事はエネルギーと同じ単位で測定できることです。 ニュートンの第二法則は力＝質量×加速度なので、力のSI単位であるニュートン（N）はM×L×T-2として導かれ、1N＝1kgm・s-2となる。 力×距離はM×L2×T-2なので、エネルギーのSI単位であるジュール（J）は1J=1kg m2 s-2と定義されます。 このとき、運動エネルギーの式は、質量（M）、長さ（または距離、L）、時間（T）という基本量の組み合わせが同じであることを自分で確認する必要があります。
熱と温度
私たちは熱や温度という言葉をよく使いますし、エネルギーの一形態として熱を語ることもよくあります。 私たちは皆、これらが何であるか直感的に理解していますが、ここではより科学的に考え、できればより正式な定義を与えたいと思います。 これは、熱に相当するエネルギーを定量化し、そこからエネルギー保存則を検証するための測定に必要な前段階である。 その結果、ある系の熱エネルギーは、その系を構成する原子や分子の運動エネルギー（上で定義したとおり）の総和にたとえることができることがわかった。 物体や系の温度は、実は構成する原子や分子の平均的な運動エネルギーの尺度なのである。 (注：温度は分子の平均運動エネルギーと正確に等しいわけではなく、正比例する。 詳しくは、運動論的分子論のページをご覧ください)。
熱と温度、およびそれらの区別の意味を視覚化する1つの方法として、ビリヤードの球のアナロジーを考えることができます。 ある簡単な文脈では、ビリヤードの玉の挙動は、気体のサンプルのような原子や分子の集まりの適切なモデルです。 気体の分子は、高速で動く手玉に打たれたビリヤードの玉のように、互いにぶつかり合ったり、容器の壁にぶつかったりして、あちこちに移動している。 ビリヤードの玉の運動エネルギーは、それぞれの玉の運動エネルギーを合計したものであり、気体分子のサンプルの熱エネルギー量と類似している。 ビリヤードのゲーム開始時の「ブレイク」では、手玉の最初の運動エネルギーがテーブル上のすべての玉に分配される。 かなり速く動いているものもあれば、そうでないものもあるが、ビリヤードの玉の系の「熱」あるいは「熱エネルギー」に例えると、これらの運動エネルギーの総和に過ぎない。 一方、ビリヤード玉の系の温度は、玉のアンサンブルの平均運動エネルギーに比例するだろう。
静電位置エネルギー
静電引力と斥力の法則（クーロンの法則）は、別の帯電物体が存在することによって帯電物体に及ぼす力を記述する。 この力は、電荷が非常に小さな点電荷として扱える場合に、最も簡単に計算することができます。 帯電物体が「感じる」力の大きさは、電荷の積（電荷のSI単位はクーロン、C）に比例し、電荷間の距離（右図ではr）の二乗に反比例します。 その力は、電荷の符号が逆であれば引力（重力と同じで、図では内向きの矢印で示す）、同じ符号であれば反発力となる。
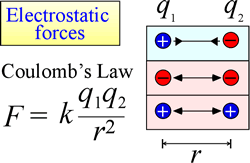
力（静電気、磁気、重力など）が離れた場所（空間を通して、機械的に接触しない）で作用できる場合、その力の影響を受ける物体を位置エネルギー場にあると言う。 先に重力ポテンシャルエネルギーについて述べたが、静電気力の場合も同様に、帯電した物体は電場の中にあることで静電気ポテンシャルエネルギーを持つことになる。 このような場は、他の電荷の近傍に存在します。
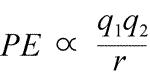
静電ポテンシャルエネルギーの式。 PE は電荷 q1 と q2 に比例し、分離距離 r に反比例します。位置エネルギー関数の形式は、力の表現であるクーロンの法則から数学的に導かれます。 離隔距離rが0に近づくと、ポテンシャルエネルギーは限りなく負になります。 同じ符号の電荷では、反発のエネルギーは常に正であり、分離距離 r がゼロに近づくと無限に正になる。
静電ポテンシャルエネルギーは化学における重要な検討事項である。 原子の性質、化学結合、分子間力の理解はすべて、系のエネルギーに寄与する電荷-電荷相互作用の影響を考慮することに絶対的に依存している。
重要な単位
エネルギー（SI 単位） 1 ジュール = 1 J = 1 kg-m-s-2
電荷、e = 1.60218 × 10-19 C （クーロン、C）
Faraday 定数。 F = NAe = 9.64853 × 104 C-mol-1
電位：ボルト、V 1 V = 1 J C-1
電位：ボルト、V 1 V = 1 J C-1