3×3行列の行列式を求める標準公式は、2×2行列の問題を小さくしたもので、非常に扱いやすくなっています。 復習が必要な場合は、2×2の行列式を求める方法についての他のレッスンをご覧ください。 ここで、正方行列 A が与えられたとします。
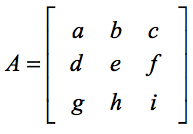
行列 A の行列式は、
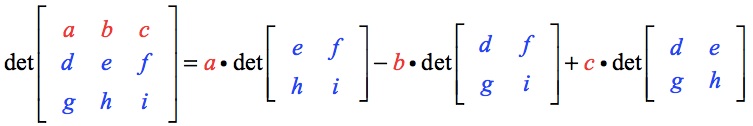
ここでキーポイントは、
- 上段の要素 a, b, c が対応する 2×2 行列へのスカラー倍として機能することに注目することです。
- スカラーaは、aを通る垂直および水平線分が引かれたときにできる余った要素の2×2行列に掛けられます。
- 同じプロセスが、スカラー乗数bとcの2×2行列を構築するために適用されています。
3×3行列の行列式(アニメーション)

3×3行列の行列式を求める例
例1: 下の3×3行列の行列式を求めなさい。
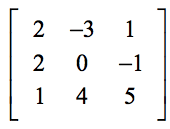
下の設定により、式の一般要素と実際の問題の要素との対応関係を見つけることができるようになります。
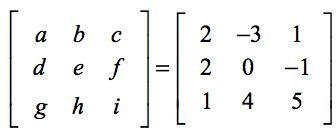
式を応用して、


例2:下の3×3行列を行列式を評価しなさい。
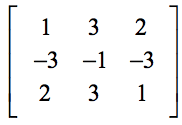
式の中の正しい場所に値を代入するときには、十分に注意してください。 よくある間違いは、値を代入する最初の段階で学生が不注意になったときに起こります。
さらに、演算も正しいかどうか、時間をかけて確認することです。 そうでないと、計算のどこかで1つでも間違いがあると、最終的に間違った答えを出すことになります。
行列式の計算は・・・
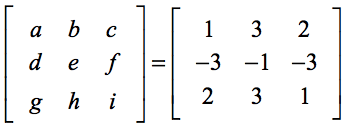
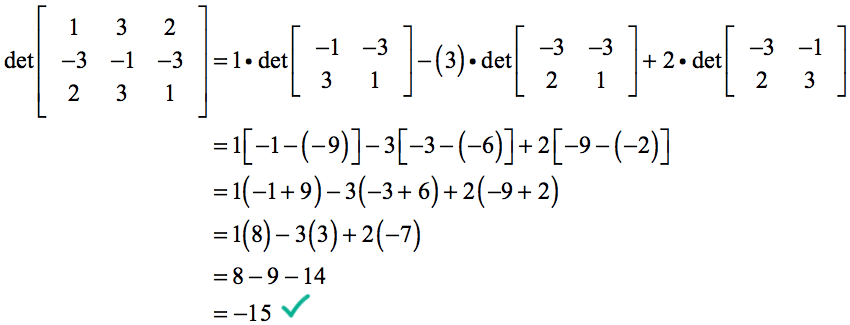
例3:下の3×3行列の行列式を解きましょう。
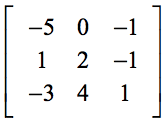
最初の行にゼロ(0)があることで、計算が非常に簡単になるはずです。 最初の行のこれらの要素は、スカラー乗算器として機能することを覚えておいてください。 したがって、ゼロが何かに乗じられると、式全体が消えてしまうことになります。