ある数式が全国紙や人気のラジオを賑わせたり、最も驚くべきことに英国議会で議論の対象となることはあまりないことです。 しかし、2003 年、私たちが学校で習った古き良き 2 次方程式は、それらすべてを兼ね備えていました。
Where we begin

それは全国教職員組合の会合で始まりました。 二次方程式は、数学者が貧しい無防備な学童に加えた残酷な拷問の例として、国民に高々と掲げられたのです。 この非難に興味を持った二次方程式は、ラジオのプライムタイムに主役として出演し、首相を相手にするのに慣れている手強いインタビュアーに質問された。 ロンドンの)タイムズ紙は、通常、現代世界の道徳的(あるいはその他の)健全性に関する重厚な議論に使われるリーダー欄のスペースを割いて、二次方程式は役に立たない、数学は役に立たない、どうせ誰も数学を勉強したくないのだから気にするな、と宣言したのである。 二次方程式による危険な入試がそのまま放置されることを懸念して、英国の存続に不可欠な二次方程式の重要性が英国下院で議論されました(肯定的な見解がとられたので、よかったと思うかもしれませんね)。
結局、どこに行き着くのでしょうか。 二次方程式は本当に死んでしまったのでしょうか? 誰も気にしていなかったのでしょうか? 数学者は本当に邪悪な怪物で、若い世代の不滅の魂を堕落させる手段として二次方程式を与えたいだけなのでしょうか。
そうかもしれませんが、本当は二次方程式のせいではないのです。 実際、二次方程式は、私たちが知っている人類の文明全体だけでなく、他の異星人の文明を発見する可能性や、衛星テレビを見るような現代の重要な活動でさえ、極めて重要な役割を担っています。 神の啓示の本質を除いて、私たちが知っている生活にこれほどの影響を与えたと考えられるものが他にあるだろうか。
The Babylonians
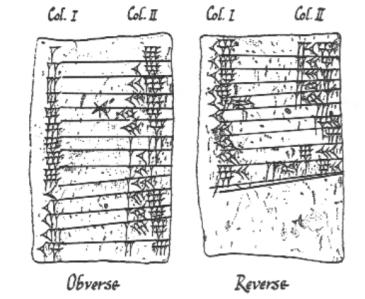
Babylonian cuneiform table recording the 9 times tables
すべては紀元前3000年頃、バビロニアで始まった。 彼らは世界最初の文明の一つで、農業、灌漑、文字などの素晴らしいアイデアを考え出した。 彼らは太陽、月、惑星の通り道をプロットし、それを粘土板に記録した(これは今でも大英博物館で見ることができる)。 バビロニア人は、現代の角度に関する考え方や、円を360度に分割する方法(1日に1度という小さな計算ミスのため)などを教えてくれたのです。 また、バビロニア人が発明した「税金取り(恐るべき)」という、あまり嬉しくない発明も、バビロニア人のおかげである。 そして、バビロニア人が二次方程式を解く必要があったのは、このことが理由の一つでした。
あなたがバビロニアの農民であるとしよう。 あなたの農場のどこかに四角い畑があり、そこで作物を育てている。 その畑で栽培できる作物の量は? 畑の一辺の長さを2倍にすると、以前の4倍の作物を栽培できることがわかります。 これは、栽培できる作物の量は畑の面積に比例し、その面積は一辺の長さの二乗に比例するからです。 数学的に言うと、 を畑の辺の長さ、
を畑の辺の長さ、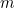 を辺長1の正方形の畑で栽培できる作物の量、
を辺長1の正方形の畑で栽培できる作物の量、 を栽培できる作物の量とします。 とすると、
を栽培できる作物の量とします。 とすると、
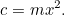 |
これが最初の二次方程式で、裸で日光に照らされて点滅しているのである。 二次方程式と面積は、同じ家族の兄弟姉妹のように結びついているのです。 しかし、今のところ、私たちは何も解かなくていいのです。 税理士は農夫に「あなたの農場の税金を払うために、 作物をください」と陽気に言うのです。 このとき、農夫はジレンマに陥った。その量の作物を育てるには、どれくらいの広さの畑が必要なのだろうか? 私たちはこの質問に簡単に答えることができます。実際、
作物をください」と陽気に言うのです。 このとき、農夫はジレンマに陥った。その量の作物を育てるには、どれくらいの広さの畑が必要なのだろうか? 私たちはこの質問に簡単に答えることができます。実際、
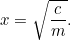 |
計算機を使用して平方根を見つけることは私たちにとって簡単ですが、バビロニア人にとってはもっと問題だったのです。 実際彼らは、現代のコンピュータが二次方程式よりはるかに難しい問題を解くのに用いるアルゴリズム(ニュートン・ラプソン法と呼ばれる)と同じ、答えへの逐次近似法を開発したのである。 ここで、農家が右図のような三角形の部分が2つあるもっと変な形の畑を持っているとしよう。
 と
と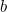 の適切な値に対して、農夫がこの畑で栽培できる作物の量は
の適切な値に対して、農夫がこの畑で栽培できる作物の量は
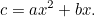 |
これは我々がよく使う二次方程式により近いような気がしてきますね。 と、税理士さんの邪推のもとでも、解くのはかなり難しい。 それでもバビロニア人は再び答えを導き出しました。 まず で割って
で割って
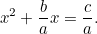 |
ここで
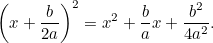 |
これを元の方程式と組み合わせると、
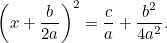 |
これが平方根を取って解決できる方程式になったのである。 その結果が、有名な「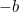 式」です。
式」です。
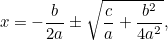 |
と書き直すと、以下のようになる。
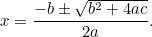 |
(式は通常「-」が付きますが、「-」が付かない場合は「-」が付きます。4ac “というのは、二次方程式は”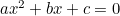 “という形で書かれるのが一般的だからです。)
“という形で書かれるのが一般的だからです。)
平方根を取ると正にも負にもなるという事実は、二次方程式が2つの解を持つという驚くべき結果につながるのです。 数学のパズルには解が1つしかないというのはこのことです。
さて、ここで二次方程式の授業はしばしば中断されます。 私たちは、数学者にインタビューするときに、すべてのジャーナリストが愛する対象、つまり数式に到達しました。 この数式に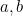 と
と の値を入れて(2つの)答えを出すという質問を無限に作ることができるのです。 しかし、これは数学の本質では全くない。 公式を見つけることは、長い道のりの第一歩に過ぎない。 その公式は何を意味するのか、その公式は宇宙について何を語っているのか、その公式を持つことは本当に重要なことなのか、と問わねばならない。
の値を入れて(2つの)答えを出すという質問を無限に作ることができるのです。 しかし、これは数学の本質では全くない。 公式を見つけることは、長い道のりの第一歩に過ぎない。 その公式は何を意味するのか、その公式は宇宙について何を語っているのか、その公式を持つことは本当に重要なことなのか、と問わねばならない。
ギリシャ人の驚き、数学的折り紙と比率の感覚
さて、1000年前の古代ギリシャ人に話を進め、彼らが二次方程式をどう作ったか見てみましょう。 ギリシャ人は優れた数学者であり、現在でも使われている数学の多くを発見している。 彼らが解くことに興味を持った方程式の一つに、(単純な)二次方程式
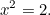 |

この方程式が解を持っているということがわかったのだ。 実際、それは長さ1の辺を持つ直角三角形の斜辺の長さである。
ピタゴラスの定理から、直角三角形の斜辺の長さが1であれば角のある三角形の短辺が と
と で、斜辺が
で、斜辺が なら
なら
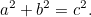 |
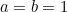 と
と を置いて
を置いて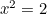 となります。 よって
となります。 よって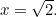
ではこの場合の は何でしょうか。 あるいは、ギリシア人の疑問として、どのような数なのだろうか? これがなぜ重要かというと、ギリシャ人の比例感覚にあった。 彼らは、すべての数は互いに比例していると考えていた。 正確には、すべての数は、<6104>と<3652>を整数としたとき、<3004>の形の分数であることを意味していた。 1/2、3/4、355/113といった数字はすべて分数の例である。 694>も分数であると考えるのは自然なことである。 大きな驚きは、そうでないことだった。 実は
は何でしょうか。 あるいは、ギリシア人の疑問として、どのような数なのだろうか? これがなぜ重要かというと、ギリシャ人の比例感覚にあった。 彼らは、すべての数は互いに比例していると考えていた。 正確には、すべての数は、<6104>と<3652>を整数としたとき、<3004>の形の分数であることを意味していた。 1/2、3/4、355/113といった数字はすべて分数の例である。 694>も分数であると考えるのは自然なことである。 大きな驚きは、そうでないことだった。 実は
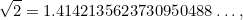 |
ここでドット は
は の10進展開を何の識別もなく無限に続けるという意味である。 (1059>
の10進展開を何の識別もなく無限に続けるという意味である。 (1059>
 は、初めて無理数(分数でも有理数でもない数)として認識された数です。 その他、
は、初めて無理数(分数でも有理数でもない数)として認識された数です。 その他、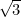 、
、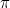 、
、 など、「ほとんどの」数字がそうである。 これらの数について考える良い方法ができるまでには、19世紀を待たなければならなかった。 694>が有理数でないという発見は、大きな興奮(結果として100頭の牛が犠牲になった)と大きなショックをもたらし、発見者は自殺を余儀なくされた。 (このとき、ギリシア人は代数をあきらめ、幾何学に転向した。
など、「ほとんどの」数字がそうである。 これらの数について考える良い方法ができるまでには、19世紀を待たなければならなかった。 694>が有理数でないという発見は、大きな興奮(結果として100頭の牛が犠牲になった)と大きなショックをもたらし、発見者は自殺を余儀なくされた。 (このとき、ギリシア人は代数をあきらめ、幾何学に転向した。
 は曖昧な数字ではなく、私たちはA4サイズの紙を使うときにいつも目にする数字です。 ヨーロッパでは、紙の大きさはAサイズで測られ、A0が最も大きく、面積は
は曖昧な数字ではなく、私たちはA4サイズの紙を使うときにいつも目にする数字です。 ヨーロッパでは、紙の大きさはAサイズで測られ、A0が最も大きく、面積は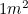 である。 このAサイズには、特別な関係があるのだ。 ここで折り紙をしてみましょう。A1の紙を半分に折ると(長い辺に沿って)、A2の紙になります。 さらに半分に折るとA3、さらに半分に折るとA4となります。 しかし、それぞれの A の大きさの比率が同じになるように、つまり、それぞれの紙が同じ形になるように、紙は設計されています。
である。 このAサイズには、特別な関係があるのだ。 ここで折り紙をしてみましょう。A1の紙を半分に折ると(長い辺に沿って)、A2の紙になります。 さらに半分に折るとA3、さらに半分に折るとA4となります。 しかし、それぞれの A の大きさの比率が同じになるように、つまり、それぞれの紙が同じ形になるように、紙は設計されています。
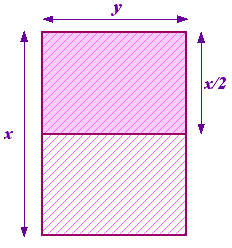
これはどのような比率なのかという問題を提起することができます。 まず、辺がxとyの紙があり、xが一番長い辺である。 これを二つに割って、今度はyが最も長い辺となる辺yとx/2の紙を作る。 これを右図に示す。
1枚目の比率は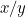 、2枚目の比率は
、2枚目の比率は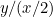 または
または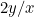 です。 この二つの割合が等しくなるようにしたい。 つまり、
です。 この二つの割合が等しくなるようにしたい。 つまり、
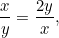 |
または
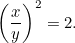 |
もう一つの2次方程式!は、2次方程式で、2次方程式の1つです。 幸いなことに、それは私たちがすでに出会ったことのあるものです。 これを解くと、
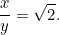 |
この結果は簡単に確認することができます。 A4(またはA3、A5)の紙を手に取り、辺の長さを測るだけです。 一枚一枚の大きさも計算できる。 A0の紙の面積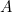 は
は
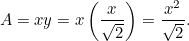 |
ですが、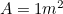 が分かっているので、A0の長辺
が分かっているので、A0の長辺 について別の2次方程式が成り立ちます。 1888>
について別の2次方程式が成り立ちます。 1888>
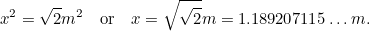
つまりA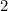 の長辺は
の長辺は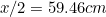 で与えられる(なぜ?となり、A
で与えられる(なぜ?となり、A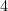 の長辺は
の長辺は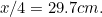 となる。 これを自分の紙で確認してみましょう。
となる。 これを自分の紙で確認してみましょう。
アメリカで使われているフールスキャップと呼ばれる紙では、この比率が異なります。 その理由を知るために、ギリシャ人の話に戻り、別の二次方程式を考えてみましょう。 それは今日でも映画のセットのデザインで続いており、自然の多くの側面で見ることができます。
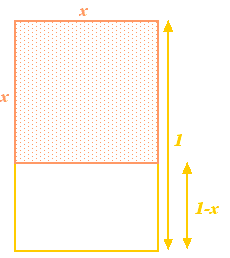
長方形から始めて、その長方形の最も短い辺と同じ辺の長さを持つ正方形を取り除きます。 長方形の最も長い辺の長さが1、最も短い辺の長さが であれば、正方形の辺の長さは
であれば、正方形の辺の長さは である。 これを長方形から取り除くと、長辺が
である。 これを長方形から取り除くと、長辺が 、短辺が
、短辺が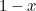 の小さい長方形になる。 ここまでは、抽象的な話だ。 しかし、ギリシア人は、上で作った大小の長方形が同じ比率になるような長方形(いわゆる黄金長方形)が最も美しい比率を持つと考えたのです。 このためには、
の小さい長方形になる。 ここまでは、抽象的な話だ。 しかし、ギリシア人は、上で作った大小の長方形が同じ比率になるような長方形(いわゆる黄金長方形)が最も美しい比率を持つと考えたのです。 このためには、
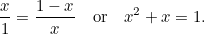 |
これも二次方程式で、あらゆる応用で出てくる非常に重要な方程式である。 これは(正の)解
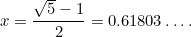 |
数  は黄金比と呼ばれて、しばしばギリシャ文字の
は黄金比と呼ばれて、しばしばギリシャ文字の 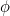 で示されることが多いのです。
で示されることが多いのです。

黄金長方形は、特にジョージアン・ハウスの窓の形に見ることができる。 最近では、写真やフィルム映像の「完全な形」としても黄金比を見ることができる。 また、ウサギの個体数の研究や、ヒマワリの種や植物の茎の葉の並び方にも二次方程式<7313>が登場する。 これらは、
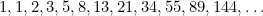 |

ひまわりの種で与えられるフィボナッチ数列を通して黄金比につながるのだ。 1059> |
黄金比を体現したパルテノン神殿 |
この列では各項は前の2項の合計となる。 15世紀、フィボナッチがウサギの将来人口を予測するために発見した。 各項とその次の項の比をとると、
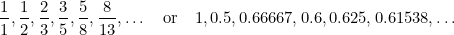 |
という数列が得られ、これらの数字は(ご存知)黄金比 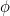 にどんどん近付いて行くのだそうです。
にどんどん近付いて行くのだそうです。
上の二次方程式の両根を求めることで、実はフィボナッチ数列の第n項の公式を見つけることができるのです。 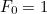 と
と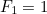 のある
のある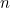 番目の数を
番目の数を とすると、
とすると、
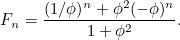 |
Conics link quadratic equations to stars

ギリシャ人は円錐の形にも非常に興味をもっていたようである。 左の絵は典型的な円錐形である。
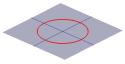
円錐の半分は、松明から出る光の広がりとして視覚化することができる。 さて、壁のような平らな面に松明を当ててみると、松明を動かしているうちにいろいろな形が見えてくるはずです。 このような形は円錐曲線と呼ばれ、円錐をさまざまな角度で切り取ったときにできる曲線のことです。 ギリシャでは、このような曲線が研究され、基本的に4種類の円錐曲線があることが分かっていた。 円錐を通る水平断面をとると円になります。 水平に対して小さな角度の断面は楕円になります。 垂直な断面を取れば双曲線、円錐の一辺に平行な断面を取れば放物線となります。 これらの曲線は、以下のように図示されています。
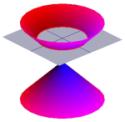 |
 |
 |
 |
|
 |
 |
 |
||
|
<4937>
|

…ellipse … |
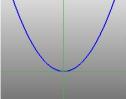
…a parabola … |
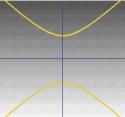
…楕円 … … |

… |
円錐曲線は、それぞれが2次方程式で記述されるので、この話が出てくるのです。 特に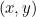 が各曲線上の点を表すとすると、
が各曲線上の点を表すとすると、 と
と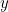 は2次方程式で結ばれる。 我々は
は2次方程式で結ばれる。 我々は
は円である。 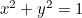 ;
;
楕円。 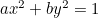 ;
;
双曲線。 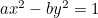 ;
;
放物線。 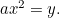
これらの曲線はギリシャ時代から知られ、研究されていましたが、円は別として、実用性はないように思われました。 しかし、次号のPlusで紹介するように、2次方程式と2次曲線の関連は、強大な幸運な偶然と相まって、宇宙の仕組みの理解につながり、16世紀には2次曲線が世界を変える時が来たのです。
著者について
クリス・バッドは、バース大学数理科学科の応用数学教授であり、ロンドンの王立研究所の数学主任である。
クリス・サングウィンは、バーミンガム大学数学・統計学部のスタッフである。
彼らは最近、オックスフォード大学出版局から出版された人気のある数学の本「Mathematics Galore! この討論の記録は、Hansard, United Kingdom House of Commons, 26 June 2003, Columns 1259-1269, 2003 にあり、House of Commons Hansard Debate ウェブサイトでオンライン公開されている
。