
概要:
Mean / Median / Mode / Variance / Standard Deviationは、データサイエンスで使われる統計学の非常に基本的な概念ですが、非常に重要な概念です。 ほぼすべての機械学習アルゴリズムでは、データの前処理にこれらの概念を使用しています。 これらの概念は記述統計学の一部であり、基本的には機械学習における特徴のためにデータを記述し、理解するために使用される
Mean :
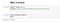
Mean は、データセット内のすべての数値の平均としても知られており、以下の式で計算される。
heights=
Median :
Median はこの順序データセットにおける中間値である。
データを昇順に並べて、その中央値を求めます。

データセットに偶数の値がある場合、中央値は中間の2つの値の合計をで割ったものになります。 2

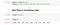
以下のようにデータセットに奇数がある場合、高さが9あるので中央値は5番目の数値になります。

Mode :
Mode は、最も頻繁に発生する数であり、データのセットで表示されています。ここでは、150が2回出現しているので、これがモードです。

Variance :
分散とは、観測値の算術平均からのばらつきを表す数値で、シグマ2乗(σ2 )で表されます。
分散は、データの集合において、グループの中の個人が平均からどの程度ばらけているかを測定します。
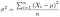
Where
Xi : Elements in the data set
mu : the population mean
=the population mean
ステップ1:この式は、データセット(母集団)から各要素を取り出し、データセットの平均から差し引くというものである。その後、すべての値を合計する。
ステップ2: ステップ1の合計を取り、要素の総数で割る。
上の式の二乗は負の符号(-)の効果を無効にする

標準偏差 :
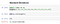
それは彼らの平均に対するデータセット内での観察の分散の尺度である。これは分散の平方根で、シグマ(σ)で表される。
標準偏差はデータセット内の値と同じ単位で表されるので、データセットの観測値がその平均からどの程度異なっているかを測定することができる。

結論: 平均値/中央値/最頻値/分散/標準偏差は、統計学においてシンプルでありながら非常に重要な概念であり、誰もが知っておくべきものです。
Want to connect :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
If you like my posts here on Medium and would hope for me to continue doing this work, consider supporting me on patreon
.