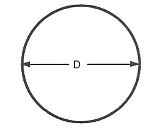
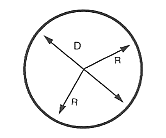
円の直径
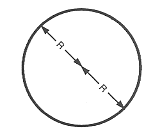
円や球の直径は半径の2倍に相当します。
$text “Diameter” = 2 ⋅ \text “Radius”$
円の円周
$text “Circumference” = 6.2832 ⋅ R$
$C = 2 ⋅ π ⋅ R$
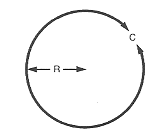
$text “Circumference, Circumference of the circle, circle of the Circumference, circle of the sphere, R$” = 6.2832 ⋅ R$
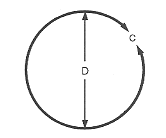
円や球の円周は直径の3.1416倍に相当する
$text “Circumference” = 3.1416 ⋅ \”Diameter”$
$C = π⋅ D$
Radius of a circle
The Radius of a circle or sphere is equals to the Diameter divided with 2.球面上の直径は、直径を2で割ると得られます。
$R = D / 2$
円の面積
円の面積は、円の半径に半径を掛け、この数字に3.1416を掛けたものに等しいです。
$text “Area” = R^2 ⋅ π$
$text “Area” = R ⋅ R ⋅ 3.1416$
この数値は、使用する測定システムによって、平方インチまたは平方ミリメートルで表されます。
円の面積は、円の直径に直径を掛けたものに、3.1416を掛けたものを4で割ったものになります。
$text “Area” = D ⋅ D ⋅ 3.1416 / 4$
$text “Area” = D^2 ⋅ π/ 4$
Area of a Cylinder
この数値は、使用する測定システムによって、平方インチまたは平方ミリメートルの単位となります。
円柱の面積は、円柱の半径の 6.2832 ( 2 × π ) 倍に、半径と高さの和を掛けたものです。1416 ⋅ R ⋅ ( R + H )$
$text “Area” = 2 π ⋅ R ⋅ ( R + H )$
この数字は、使用する測定システムに応じて、平方インチまたは平方ミリメートルで表示されます。
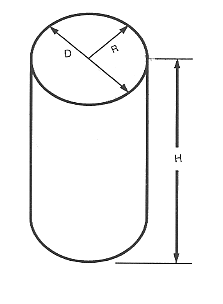
円柱の体積
円柱の体積は円柱の半径に半径を掛け、この数に3・1416をかけて、この数字に円柱の長さを掛けます
$text “Volume” = 3.1416 ⋅ R ⋅ R ⋅ H$
$text “Volume” = π⋅ R^2 ⋅ H$
この数値は、使用する測定システムに応じて、立方インチまたは立方ミリメートルで表示されることになります。
Area of a Sphere
The Area of a Sphere is equal to the Square of the Radius by 12.566 ( 4 × π ) or Pi times the Diameter squared ( π × D × D ).
$TEx “Area” = 12.566 ⋅ R ⋅ R$
$text “Area” = 4 ⋅ π ⋅ R^2$
$text “Area” = π ⋅ D^2$
この数字は、使用する測定システムによって、平方インチまたは平方ミリメートルに置き換えられます。
Volume of a Sphere
Sphere of a Volumeは球体の半径に再び半径を掛けたものである。 そしてこの数値にまた半径を掛ける。 そして、この数字に12.566を掛け、その結果を3で割ります。
$text “Volume” = 12.566 ⋅ R ⋅ R ⋅ R / 3$
$text “Sphere Volume” = 4 ⋅ π ⋅ r^3 = ( π ⋅ d^3)/6$
この数値は、使用する測定システムに応じて、立方インチまたは立方ミリメートル単位となる
$text “Volume” = 4/3 ⋅ R R ⋅ R ⋅ R / 3$
$text “Volume” = 4 3$
$text” Volume” = 4 ⋅ R R ⋅ R/R/ 3 $
$tex “Sphere” = 4.566 ⋅ π ⋅ ⋅ π ⋅ d^3