学習目標
- 区分線形関数への導入
- 区分線形関数を定義する。 関数
- 区分関数を評価する
- アプリケーションが与えられたら区分関数を書く
- グラフ区分関数
- 区分関数が与えられたら定義された関数です。 sketch a graph
- Write domain and range of a piecewise function given a graph
関数の中にはバラバラになっているものがあります。 この項では、本質的に離散的な断片の集まりである関数を定義し、グラフ化する方法について学びます。 このように定義されるものの例としては、車のプロファイルの設計、携帯電話のプランの把握、所得税率の計算などがあります。 例えば、税率は所得によって異なり、下表のように所得の幅があっても同じになります。
| 限界税率 | 独身者の課税所得 | 夫婦合算申告または適格寡婦(者)課税の場合 5062> | 夫婦別姓課税所得 | 世帯主課税所得 |
|---|---|---|---|---|
| 10% | $0 – $9,275 | $0 – $18,550 | $0 – $9,275 | $0 – $13,250 |
| 15% | $9,276 – $37,650 | $18,551 – $75,300 | $9,276 – $37,650 | $13,251 – $50,400 |
| 25% | $37,651 – $91,150 | $75,301 – $151,900 | $37,651 – $75,950 | $50,401 – $130,150 |
| 28% | $91,151 – $190,150 | $151,901 – $231,450 | $75,951 – $115,725 | $130,151 – $210,800 |
| 33% | $190,151 – $413,350 | $231,451 – $413,350 | $115,726 – $206,675 | $210,801 – $413,350 |
| 35% | $413,351 – $415,050 | $413,351 – $466,950 | $206,676 – $233,475 | $413,351 – $441,000 |
| 39.6% | $415,051+ | $466,951+ | $233,476+ | $441,001+ |
区分関数とは領域の異なる断片にわたって出力を定義するのに複数の数式が使用されている関数である。
入力値が特定の “境界” を横切るとルールや関係が変化するような状況を説明するために区分関数を使用します。 たとえば、ビジネスでは、注文数がある値を超えると、特定のアイテムのピースあたりのコストが割り引かれる状況によく遭遇します。 また、税額計算も区分関数の一例である。 例えば、所得が1万ドルまでは10%、それ以上は20%という単純な税制を考えてみよう。 総所得 S に対する税金は、S が 10,000 ドルなら 0.1S で、S> 10,000 ドルなら 1000 + 0.2 (S – $10,000) となる。
Piecewise Function
区分関数とは、出力を定義するのに複数の公式が使われる関数である。 各式はそれ自身の領域を持ち、関数の領域はこれらすべての小さい領域の和となる。 この考え方を以下のように表記する。
fleft(xxxright)=BEGIN{CASE} CONTEXT {formula 1 if x is in domain 1} \text{formula 2 if x is in domain 2} ◇end{CASE} ◇ext{formula 3 if x is in domain 3} ◇ext{formula 2 if x is in domain 3] ◇ext {formula 2 if x is in domain 1] ◇ext {Formula 2 if x is in domain 2} ◇ft {Formula 3 if x is in domain 2} ◇ft {Formula 3 if x is in domain 3
区分的表記で絶対値関数は
Evaluate a Piecewise Defined Function
最初の例では区分的定義関数の評価方法を説明します。 入力を評価するためにどの式を使用するかを決定するために、ドメインに注目することがいかに重要であるかに注意してください。
例
与えられた関数
f(x)=begin{cases}7x+3text{ if }x<0\7x+6text{ if }xge{0}end{cases},
evaluate.Generated。
- f (-1)
- f (0)
- f (2)
次のビデオでは、区分的に定義された関数からいくつかの値を評価する方法を紹介します。
次の例では、電話会社のデータ転送コストをモデル化した関数を評価する方法を示します。
例
ある携帯電話会社が以下の関数を使用して、データ転送のギガバイトに対するコストC(ドル)を決定しています。
Find the cost of using 1.0 Gバイトのコストを求める。9420>
解の解析
この関数は下のグラフで表されます。 g=2で関数が定数から正の傾きを持つ直線に変化するところがわかります。 それぞれの公式が適切な領域で適用されていることを確認しながら、異なる公式のグラフを共通の軸にプロットしていきます。

C(g) = Centaleft(gentaright)=Centabegin{cases}{25}text{ if }{ 0 }<{ g }<{ 2 }text{ if }{ g}ge{ 2 }}end{cases}
区分的定義関数を書く
最後の例では、ガイド付き博物館ツアーの価格をモデル化する区分的定義関数を書く方法を紹介します。
例題
ある博物館が1~9人のグループでガイドツアーを行う場合、1人あたり5ドル、10人以上のグループの場合は50ドルの固定料金を徴収している。 人数nと費用Cを関連付ける関数を書きなさい。
Analysis of the Solution
図21に関数が表されています。 グラフはn=0からn=10までは対角線、それ以降は定数である。 この例では、2つの式はn=10という会合点で一致していますが、すべての区分関数がこの性質を持つわけではありません。

次のビデオでは、シナリオが与えられた区分定義関数を書く例を示します。
区分関数が与えられたら式を書き、各区間のドメインを特定しなさい。
- 異なるルールが適用される区間を特定する。
- 各区間の入力から出力を計算する方法を記述する式を決定する。
Graph Piecewise Functions
このセクションでは、区分関数をプロットします。 下にプロットした関数は、ある携帯電話会社のデータ転送にかかる費用を表しています。 関数が定数から、g=2で正の傾きを持つ直線に変化するところがわかります。 区分関数をプロットするとき、各式が適切な領域で適用されていることを確認することが重要です。Cleft(gentaright)=Chenbegin{cases}{25} \この場合、0から2までの入力に対して25が出力されます。

区分関数が与えられたら、グラフを描く。
- 領域の各断片上の区間が定義する境界をx軸で示す。
- 領域の各断片について、その断面に対応する方程式を使用して区間でグラフ化する。 関数の基準に違反するので、1つの区間上で2つの関数をグラフにしないでください。
例題
関数のグラフを描く。
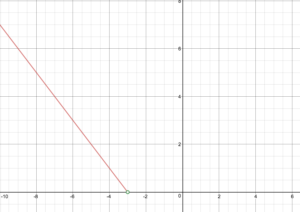
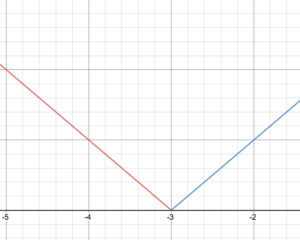
Given the piecewise definition f(x)=begin{cases}-x – 3}text{ if }x < -3\ x + 3}text{ if }. x \ge -3end{cases}
Draw graph of f.
State domain and range of function.
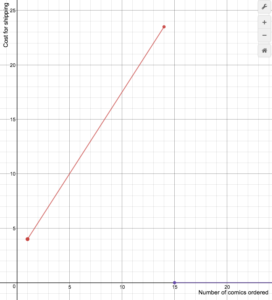
次の例では、オンラインコミック本の小売業者の送料をモデル化した区分け定義関数をグラフ化します。
例題
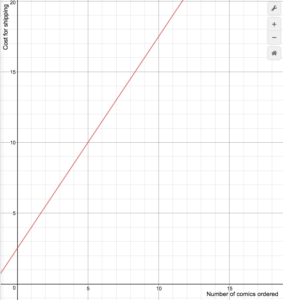
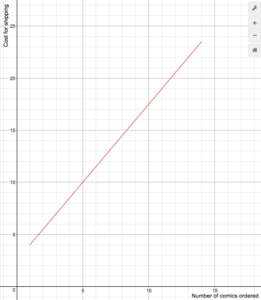
あるオンラインコミック本の小売業者は、以下の式
S(n)=Cases}1.5n+2 に従って配送料を請求している。5text{ if }1le{n}le14}0text{ if }n}ge15}end{cases}
Draw a graph of the cost function.