符号付き整数の足し算と引き算を視覚化するために、数直線をモデルとして使用することができます。 足し算と引き算を数直線上の方向と考えればよいのです。 また、これらの基本的な演算をどのように行うかを定義するいくつかの規則や性質があります。
同じ符号を持つ整数を足すには、同じ符号のまま、それぞれの数値の絶対値を足す。
異なる符号を持つ整数を足すには、最大の絶対値を持つ数の符号を維持し、最大の絶対値から最小の絶対値を引く。
整数を引くにはその反対を加える。
注意! 負数の負は反対の正数です。 つまり、実数の場合、
-(-a) = +a
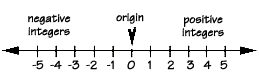
ここで、二つの正の整数を足す方法を説明します:
4 + 7 = ?
数直線で正の4から始めて右に7単位移動すると、正の11に行きつきます。 また、これらの整数は符号が同じなので、符号をそのままにして、その絶対値を足せば、同じ答えの正の11になります。
ここで、2つの負の整数を足す方法について説明します。
-4 + (-8) = ?
数直線上のマイナス4から始めて8単位左に移動すると、マイナス12になります。 また、これらの整数は同じ符号なので、負の符号のまま、その絶対値を足せば、同じ答えのマイナス12になります。
ここで、正の整数を負の整数に足す方法を説明します。
-3 + 6 = ?
実数線上のマイナス3から始めて、右に6個移動すると、プラス3までいきます。 また、これらの整数は符号が異なるので、
絶対値の大きい方の整数の符号を残し、絶対値の小さい方を大きい方から引くとよいでしょう。
6から3を引き、正の符号を残して、やはり正の3を与えます。
ここで、正の整数に負の整数を足す方法を説明します。
5 + (-8) = ?
実数直線上の正の5から始めて8単位左に移動すると、負の3に行き着くのです。 また、これらの整数は符号が異なるので、絶対値の大きい方から符号を残して絶対値の小さい方を引くか、8から5を引いて負の符号を残せば、やはり負の3が得られます。
5 – 8 = ?
同じ結果になるので、5から8を引くことは正の5に負の8を足すことと同じであることがわかる。 答えは-3です。
ある数を引くには、その反対を足します。