- 幾何学の表
- 学習目標
- KEY TAKEAWAYS
- Key Points
- 主要な用語
- VSEPR モデル
- How to Determine Molecular Geometry(分子形状の決定方法) – YouTube。 このビデオでは、単純な分子の主要な幾何学的形状をすばやく見つけるための1つの方法を説明しています。
- Molecular Geometries
- 学習目標
- KEY TAKEAWAYS
- Key Points
- 主要な用語
- AXE 法
- Main geometries (without lone pairs of electron):
- Trigonal Planar
- Tetrahedral
- Octahedral
- Interactive: 電子の幾何学。 分子は、共有電子と非共有電子のパターンによって、さまざまな形状をとります。 1543> Lone Electron Pairs
- 学習目標
- KEY TAKEAWAYS
- Key Points
- 主要な用語
- Lone Pair Electrons
- 配位数と中心原子
- The Repulsive Effect of the Lone Pair Electrons
- Interactive: 非共有電子と「曲がった」形。 1543> LICENSES AND ATTRIBUTIONS CC LICENSED CONTENT, SHARED PREVIOUSLY Curation and Revision (改訂版)。 提供元 Boundless.com。 ライセンス CC BY-SA: 帰属-継承 CC LICENSED CONTENT, SPECIFIC ATTRIBUTION VSEPR Theory.Planet。 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/VSEPR_Theory. ライセンス CC BY-SA: 帰属-継承 分子幾何学. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/Molecular_geometry. ライセンス CC BY-SA: 帰属-継承 VSEPR Theory. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/VSEPR%20Theory. ライセンス CC BY-SA: 帰属-継承 分子幾何学. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/Molecular_geometry. ライセンス パブリックドメイン。 既知の著作権なし VSEPR geometries. 提供元 ウィキメディア 場所は http://commons.wikimedia.org/wiki/File:VSEPR_geometries.PNG. ライセンス CC BY-SA: 帰属-継承 How to Determine Molecular Geometry(分子形状の決定方法) – YouTube。 場所は次の通り。 http://www.youtube.com/watch?v=pA9ML0HVOYE. ライセンスは パブリックドメイン。 既知の著作権はありません。 ライセンス条件 標準YouTubeライセンス Linear-3D-balls. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/File:Linear-3D-balls.png. ライセンス CC BY: 帰属 分子幾何学。 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/Molecular_geometry. ライセンス CC BY-SA: 帰属-継承 VSEPR Theory. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/VSEPR_Theory. ライセンス CC BY-SA: 帰属-継承 VSEPR Theory. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/VSEPR%20Theory. ライセンス CC BY-SA: 帰属-継承 分子幾何学. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/Molecular_geometry. ライセンス パブリックドメイン。 既知の著作権なし VSEPR geometries. 提供元 ウィキメディア 場所は http://commons.wikimedia.org/wiki/File:VSEPR_geometries.PNG. ライセンス CC BY-SA: 帰属-継承 How to Determine Molecular Geometry(分子形状の決定方法) – YouTube。 場所は次の通り。 http://www.youtube.com/watch?v=pA9ML0HVOYE. ライセンスは パブリックドメイン。 既知の著作権はありません。 ライセンス条件 標準YouTubeライセンス Linear-3D-balls. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/File:Linear-3D-balls.png. ライセンス CC BY: 帰属 VSEPR Theory. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/VSEPR_Theory%23AXE_method. ライセンス パブリックドメイン。 既知の著作権なし VSEPR Theory. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/VSEPR_Theory%23AXE_method. ライセンス パブリックドメイン。 既知の著作権なし 調整番号。 提供元 ウィクショナリー。 所在地は http://en.wiktionary.org/wiki/coordination_number. ライセンス CC BY-SA: Attribution-ShareAlike John Hutchinson, Concept Development Studies in Chemistry. 2013年9月18日。 提供元 OpenStax CNX。 所在地は http://cnx.org/content/m12594/latest/?collection=col10264/latest. ライセンス CC BY: 帰属 Boundless. によって提供される。 バウンドレス・ラーニング。 所在地は http://www.boundless.com//chemistry/definition/lone-pair. ライセンス CC BY-SA: 帰属-継承 Molecular geometry. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/Molecular_geometry. ライセンス パブリックドメイン。 既知の著作権なし VSEPR geometries. 提供元 ウィキメディア 場所は http://commons.wikimedia.org/wiki/File:VSEPR_geometries.PNG. ライセンス CC BY-SA: 帰属-継承 How to Determine Molecular Geometry(分子形状の決定方法) – YouTube。 場所は次の通り。 http://www.youtube.com/watch?v=pA9ML0HVOYE. ライセンスは パブリックドメイン。 既知の著作権はありません。 ライセンス条件 標準YouTubeライセンス Linear-3D-balls. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/File:Linear-3D-balls.png. ライセンス CC BY: 帰属 VSEPR Theory. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/VSEPR_Theory%23AXE_method. ライセンス パブリックドメイン。 既知の著作権なし VSEPR Theory. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/VSEPR_Theory%23AXE_method. ライセンス パブリックドメイン。 既知の著作権なし VSEPR Theory. 提供元 ウィキペディア 所在地は http://en.wikipedia.org/wiki/VSEPR_Theory. ライセンス パブリックドメイン。 既知の著作権なし Tetrahedral_Structure_of_Water.png. 提供元 ウィキメディア 場所は https://commons.wikimedia.org/wiki/File:Tetrahedral_Structure_of_Water.png. ライセンス。 パブリックドメイン。 既知の著作権なし 個々の分子の形状を予測するために使用する化学モデルで、電子-電子-電子に基づいている。静電反発 分子またはイオン内の中心原子に直接隣接する原子の総数 共有結合を形成するために使用されていない2つの(1対の)価電子
幾何学の表
VSEPR理論は分子の幾何学(線形、三角形、三角両錐体、四面体、八面体)を決定します。
学習目標
VSEPRモデルを適用して、中心原子に孤立電子がない分子の幾何学的形状を決定する。
KEY TAKEAWAYS
Key Points
- 基本的に、VSEPRモデルは、負の電荷の領域が互いに反発し、それら(およびそれらが形作る化学結合)をできるだけ遠くに離すことを理論的に示しています。
- 単独対電子を持たない主な幾何学は、線形、三角形、四面体、三角両錐体、および八面体である。
主要な用語
- VSEPR理論: 電子対の静電反発に基づいて個々の分子の形状を予測するために使用される化学モデル
VSEPR モデル
価電子殻電子対反発 (VSEPR) モデルでは、2 つ以上の他の原子と接続している原子の最外殻(価電子)にある結合および非結合電子対に焦点を当てます。
基本的に、VSEPR モデルでは、これらの負の電荷の領域は互いに反発し、それら(およびそれらが形成する化学結合)はできるだけ離れているようになると理論化しています。 したがって、単純な三原子分子![]() に含まれる2つの電子雲は、反対方向に伸びることになる。 180 度の角度分離は、2 つの結合軌道をできるだけ互いに遠ざける。したがって、2 つの化学結合が反対方向に伸びて、線形分子を生み出すと予想される
に含まれる2つの電子雲は、反対方向に伸びることになる。 180 度の角度分離は、2 つの結合軌道をできるだけ互いに遠ざける。したがって、2 つの化学結合が反対方向に伸びて、線形分子を生み出すと予想される

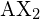 の線形化合物を表しています。
の線形化合物を表しています。 中心原子が 1 対以上の非結合電子も含む場合、これらの負電荷の追加領域は、結合原子に関連するものとほぼ同じように動作します。 価電子帯のさまざまな結合および非結合ペアを含む軌道は、相互反発を最小化する方向に中心原子から伸びることになります。 中心原子が部分的に占有された d 軌道を持つ場合、5 つまたは 6 つの電子対を収容することができ、「拡大八面体」と呼ばれるものを形成することがある。 VSEPR理論による幾何学的形状の表は、分子の描画や理解を容易にすることができる。 分子形状の表は、第1図にあります。 第2図は、この表の視覚的な補助となるものである


How to Determine Molecular Geometry(分子形状の決定方法) – YouTube。 このビデオでは、単純な分子の主要な幾何学的形状をすばやく見つけるための1つの方法を説明しています。
Molecular Geometries
The VSEPR theory describes five main shapes of simple molecules: linear, trigonal planar, tetrahedral, trigonal bipyramidal, and octahedral.これは、単純分子の5つの主要な形状を説明します。
学習目標
VSEPRモデルを適用して、中心原子が1つ以上の孤立電子を含む分子の形状を決定する。
KEY TAKEAWAYS
Key Points
- 線形:タイプ
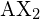 の単純三原子分子、その二つの結合軌道は180°離れている。
の単純三原子分子、その二つの結合軌道は180°離れている。 - 三角平面:三角で一平面上にあり、結合角は120°である。
- 四面体:中心原子1個に4つの結合があり、結合角は109.5°。
- 三角両錐:中心原子の周りに5つの原子があり、結合角120°の平面上に3つと分子の反対端に2つ。
- オクタヘドル:中心原子の周りに6つの原子、すべての結合角は90°である。
主要な用語
- VSEPR理論:電子対の静電反発の程度に基づいて個々の分子の形状を予測するために、価電子殻電子対反発(VSEPR)モデルを使用します
AXE 法
分子形状の別の見方は、電子数の「XE法」による方法です。 AXEのAは中心原子を表し、常に暗黙のうちに添え字1がつきます。Xは中心原子と外部原子間のシグマ結合の数(複数の共有結合-二重、三重など-を1Xと数える)、Eは中心原子を取り巻く孤立電子対の数です。 XとEの和は立体数として知られ、価電子結合理論で用いられる混成軌道の総数にも関連している。 VSEPRは立体数およびXとEの分布から分子の幾何学的形状を予測する。

なお、幾何学は電子配置ではなく、原子位置のみによって名付けられる。

Main geometries (without lone pairs of electron):
線形モデルでは、原子は直線で結ばれ、結合角は単に隣接する二つの結合間の幾何学的角度となる。 ![]() 型の単純な3原子分子は、その2つの結合軌道が180°離れている。 VSEPR理論で直線状になる三原子分子の例としては、
型の単純な3原子分子は、その2つの結合軌道が180°離れている。 VSEPR理論で直線状になる三原子分子の例としては、![]() (オクテット則に従うだけの電子を持たない)や
(オクテット則に従うだけの電子を持たない)や![]() がある。 二酸化炭素の電子点式を書くとき、C-O結合が二重結合であることに注意してください。 中心の炭素原子は他の2つの原子と結合していることに変わりはない。 2つの酸素原子を結ぶ電子雲は180°離れている。
がある。 二酸化炭素の電子点式を書くとき、C-O結合が二重結合であることに注意してください。 中心の炭素原子は他の2つの原子と結合していることに変わりはない。 2つの酸素原子を結ぶ電子雲は180°離れている。

Trigonal Planar
三角形の平面状の分子は、三角形で一面、つまり平らな面を持っています。 ![]() のような
のような ![]() 分子は、中心原子から3つの電子密度領域が伸びている。 5860>
分子は、中心原子から3つの電子密度領域が伸びている。 5860>
Tetrahedral
Tetra-は4つ、-hedralは固体の面を意味し、「四面体」は文字通り「4つの面を持つ」という意味である。 「この形状は、1つの中心原子に4つの結合があり、孤立電子対が存在しない場合に見られる。 VSEPR理論によると、電子結合間の結合角は109.5oである。 四面体分子の例として、メタン![]() がある。 4つの等価な結合が3次元的に4つの方向を向いており、炭素原子を中心とした四面体の4つの角に相当する。
がある。 4つの等価な結合が3次元的に4つの方向を向いており、炭素原子を中心とした四面体の4つの角に相当する。

三角両錐型は分子中で中心原子が5つの原子で囲まれる時に形成される。 この形状では、3つの原子は結合角120°の同一平面上にあり、他の2つの原子は分子の反対側の端にある。 周期表第15族の元素で![]() 型の化合物を形成するものがあり、
型の化合物を形成するものがあり、![]() や
や![]() がその例である。
がその例である。

Octahedral
Octa- は 8 を意味し、-hedral は固体の面に関係するので、「八面体」は文字通り「8つの面を持つ」という意味です。 結合角はすべて90°で、4つの電子対が四面体の角に向かうと反発が最小になるように、6つの電子対は八面体の角に向かおうとする。 八面体分子(![]() )の例として、六フッ化硫黄(
)の例として、六フッ化硫黄(![]() )があります。
)があります。
https://lab.concord.org/embeddable.html#interactives/jsmol/electron-geometry.json
Interactive: 電子の幾何学。 分子は、共有電子と非共有電子のパターンによって、さまざまな形状をとります。 1543>
Lone Electron Pairs
Nonbonding electrons are in orbitals that occupy space, repel the other orbitals, and change a molecule’s shape.これらの例では、分子の形に影響を与えるすべての電子は、原子を一緒に保持している共有結合の中で共有されています。
学習目標
分子の形状に対する孤立電子対の影響を認識する。
KEY TAKEAWAYS
Key Points
- 価電子殻の様々な結合・非結合対を含む軌道は、中心原子からその反発を最小限にする方向に伸びるでしょう。
- 非結合軌道は、その遠端に電子雲を引き寄せる原子核がないため、そのような軌道の電荷は中心原子の近くに集中することになります。
主要な用語
- 配位数:化学および結晶学において、分子または結晶中の中心原子の隣接数
- ローン・ペア。
Lone Pair Electrons
これまで、Lone Pair Electronsのない幾何学的形状のみを論じてきました。 幾何学の表やAXE法でお気づきのように、孤立対を加えると分子の形が変わります。 中心原子にも1対以上の非結合電子がある場合、これらの負電荷領域は結合原子と同じような振る舞いをすることは前述したとおりです。 5860>

配位数と中心原子
配位数とは、ある原子(しばしば中心原子と呼ばれる)を囲む電子対の数のことです。 ローンペアは分子の中で何もない空間のように見えるので、ローンペアを持つ分子と持たない分子の形状は異なってきます。
水分子(![]() )の場合、中心原子は
)の場合、中心原子は![]() で、ルイス電子のドット式では非結合電子が2対あることが予測されます。 したがって、酸素原子は四面体配位することになり、四面体の中心に位置することになる。 配位位置のうち2つはO-H結合を構成する共有電子対で占められ、残りの2つは非結合電子対で占められる。 したがって、酸素原子は四面体配位していますが、
で、ルイス電子のドット式では非結合電子が2対あることが予測されます。 したがって、酸素原子は四面体配位することになり、四面体の中心に位置することになる。 配位位置のうち2つはO-H結合を構成する共有電子対で占められ、残りの2つは非結合電子対で占められる。 したがって、酸素原子は四面体配位していますが、![]() 分子の結合形状(形)は曲がっていると表現されます。
分子の結合形状(形)は曲がっていると表現されます。

The Repulsive Effect of the Lone Pair Electrons
There is a important difference between bonding and non-bonding electron orbitals. 非結合軌道には電子雲を引き寄せる原子核が端にないため、そのような軌道の電荷は中心原子に集中します。その結果、非結合軌道は結合軌道よりも他の軌道に反発を与えます。 ![]() では、2つの非結合軌道が結合軌道を押しやり、H-O-H角が四面体角の109.5°ではなく104.5°になっています。
では、2つの非結合軌道が結合軌道を押しやり、H-O-H角が四面体角の109.5°ではなく104.5°になっています。
電子ドット構造の![]() では、窒素原子の価電子殻に非結合電子を1組配置しています。 これは窒素の周りに3つの結合原子と1つの孤立対があり、配位数は4となり、
では、窒素原子の価電子殻に非結合電子を1組配置しています。 これは窒素の周りに3つの結合原子と1つの孤立対があり、配位数は4となり、![]() で起こったのと同じです。
で起こったのと同じです。

 のルイスドット構造…。
のルイスドット構造…。 したがって、3つの水素原子は窒素原子を中心とした四面体の角に位置することが予測されます。 ローンペア軌道は四面体の4番目の角を指しますが、その位置は空いているので、![]() 分子自体は四面体にはならず、ピラミッド型、より具体的には三角錐(三角形の底面を持つピラミッド)の形状を取ります。 水素原子はすべて同一平面上にあり、窒素はその外側にある。
分子自体は四面体にはならず、ピラミッド型、より具体的には三角錐(三角形の底面を持つピラミッド)の形状を取ります。 水素原子はすべて同一平面上にあり、窒素はその外側にある。
ローンペアを含む5配位分子では、これらの非結合軌道(中心原子に近いため、他の軌道に反発しやすい)は、優先的に赤道面に存在するようになります。 このため、軸方向に配向した2つ以下の結合軌道に対して、90°の角度を持つように配置される。 したがって![]() のような
のような![]() 分子(中心原子Aが他の4つの原子Xと1つの非結合電子対に配位している分子)は「シーソー」型になると予測できます。
分子(中心原子Aが他の4つの原子Xと1つの非結合電子対に配位している分子)は「シーソー」型になると予測できます。

結合原子を非結合原子に置き換えることで、三角形の二角錐の配位がさらに単純な分子形状になります。
https://lab.concord.org/embeddable.html#interactives/jsmol/unshared-electrons.json