まず、指数による値の分割について説明します。
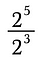
指数は乗法の繰り返しを表します。 つまり、上の式は次のように書き換えられます:
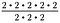
2/2 = 1なので、2/2を3組打ち消します。 これで2-2、つまり2の2乗が残る。
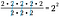
もちろん近道で、上の2の数から下の2の数を引くことができる。 これらの量はそれぞれの指数で表されるので、指数値の差を乗として共通の底を書けばよいのです。
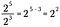
この規則を一般化すると、次のようになります。nは0以外の実数、xとyも実数で表す場合です。
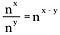
Exploring the Zero Power
ここからなぜ0以外の数を0乗すると1になるか、という説明が簡単に導き出される。 もう一度、具体例を見てみましょう。
0でない数をそれ自体で割ると1になることは分かっています。 ですから、次のように書けます。
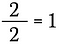
これは書くのと同じことです。
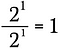
さて、先ほどの指数法則を利用して、この式の左辺を書き換えてみましょう。
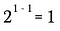
もちろん、これと同等である。
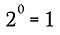
この例と同じ過程を、上の一般化規則と一緒に使えば、ゼロ以外の実数をゼロ乗すると1になることを示すことができます。
What about Zero to the Zero Power?
ここからが厄介なところです。 上の方法が破綻するのは、もちろんゼロで割ることはダメだからです。
まず、よくあるゼロの割り算のエラーから見ていきましょう。
2÷0はどうでしょうか? なぜできないのかを見てみましょう。
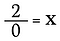
割り算は本当は掛け算の一種ですから、上の式を書き換えるとどうなるでしょうか。
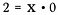
xについてこの方程式を満たすのはどんな値でしょうか。
値などない! どんな数でも0倍すると0になり、2にはなりえません。 したがって、ゼロによる除算は不定であると言います。
次に0÷0を見てみましょう。
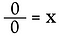
もう一度、乗法の問題として書き直します。
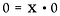
ここで、非常に異なる状況に遭遇します。 xの解はどんな実数でもよいのです! x が何であるかを決定する方法はありません。
ゼロを基点として上記の方法でゼロの0乗を決定しようとすると、0÷0≠1であることは分かっているが不確定なので、すぐに停止してしまい続けることができないのです。 1と定義すべきと考える人もいれば、0と考える人もおり、また、定義されないと考える人もいます。 これにもかかわらず、数学界は少なくともほとんどの目的のために、ゼロの0乗を1と定義することに賛成しています。
おそらく、素人の数学者にとって役に立つ指数の定義は次のとおりです。