小学4年生のアリスさんからの質問「10角形の対角線は何本でしょう」
いい質問ですね、アリスさん。 しかし、その質問の答えを与える代わりに、自分で計算する方法をお見せします。 それだけでなく、どんな多角形でも、20辺でも50辺でも2000辺でも、その答えがわかる方法を紹介します!
準備はいいかい? まず、簡単な例から始めよう。 ここでは、8つの辺を持つ多角形(8角形と呼ばれる)を例にします。
さて、この多角形は、8つの辺を持っているので、頂点も8つあります。 すべての対角線を把握しようとすると、ちょっと無理があるように思いますので、1つの頂点に注目してみましょう。 八角形で、1つの頂点から始まる対角線はいくつ描けるでしょうか。
答えは5本です。 下の図を見てください。

この図では、一番上の頂点のすぐ下の左側の対角線を選び、対角線を引けるすべての頂点に対角線を引きました。 どの対角線に対角線を引くことができないのでしょうか。 ある頂点からそれ自身に戻る対角線は引けませんし、その頂点の隣の 2 つの頂点にも対角線を引けません (それは対角線ではなく、辺になるからです!)。 合計8個の頂点から、対角線を引けない3個の頂点を引いて、残り5個の頂点です。 これは重要なことで、頂点の数から3を引くと、どの頂点からでも引ける対角線の数になります。
しかし、これは1つの頂点だけです! どの頂点からも対角線は引けるんですよね? もちろん! この八角形には8つの頂点がありますから、1頂点あたりの対角線の数をとって、それを頂点の数でかけばいいんです。 5 x 8 = 40.
これが答えだと思いたいかもしれませんが、そうではありません。 なぜ違うのでしょうか。 なぜなら、すべての対角線を2回数えてしまったからです。 すべての対角線は2つの頂点を持っているので、一方の端から数えて、もう一方の端からも数えているのです。 ですから、実際の対角線の数を知るには、答えを2で割る必要があります。
この推理を、2000辺の多角形で試してみましょう。 さて、2000角形の絵を描くつもりはありません。絵がなくても推論ができるようにしましょう。
- 頂点を選んでください。 その頂点から対角線を何本引けるか? 答え:2000 – 3 = 1997.
- 頂点は全部でいくつでしょう? 答え:2000
- すべての頂点から数えた対角線はいくつでしょう? 答え 1997×2000=3,994,000
- おっと! 各対角線を2回ずつ数えてしまった! 重複をなくすにはどうしたらよいでしょうか。 答えは 3994000 / 2 = 1,997,000
つまり、2000角形は199万7000個の対角線を持っています!
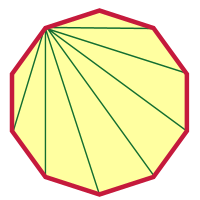
2000角形のように狂ったことをした後は、10角形をそんなに難しく感じないはずでしょう? 私が始めてあげるから、ここから仕上げてね。 頂点を選んで、その頂点から対角線を引いていくんだ
いくつあるんだ? 絵を見ずに何個あるかわかりましたか?
ここからわかりますか? そうだといいんですけどね〜。 アリスさん、がんばってください。
ちなみに、使える公式があり、こんな感じです。 D = n(n – 3)/2です。 でも、正直なところ、私は生徒たちがこれを暗記することは期待していません。 ただ、正直なところ、これを暗記してほしいとは思っていません。 理屈がわかれば、公式があるよりもっといい!