Half Adder and Full Adder Circuit
Half Adder and Full Adder circuits is explained with their truth tables in this article. Der Entwurf eines Volladdierers mit einer Halbaddiererschaltung wird ebenfalls gezeigt. Ein-Bit-Volladdierer-Schaltung und Multi-Bit-Addition mit Volladdierer wird auch gezeigt.
Bevor wir in dieses Thema einsteigen, ist es sehr wichtig, etwas über Boolesche Logik und logische Gatter zu wissen.
Sieh dir das an: Boolesche Logik
Sieh dir das an: Logische Gatter
Sieh dir das an: FLIP FLOPS
Was ist ein Addierer?
Ein Addierer ist eine Art Taschenrechner, der zum Addieren von zwei Binärzahlen verwendet wird. Wenn ich Taschenrechner sage, meine ich nicht einen mit Tasten, sondern eine Schaltung, die mit vielen anderen Schaltungen für eine breite Palette von Anwendungen integriert werden kann. Es gibt zwei Arten von Addierern:
- Halbaddierer
- Volladdierer
Halbaddierer
Mit Hilfe des Halbaddierers können wir Schaltungen entwerfen, die in der Lage sind, eine einfache Addition mit Hilfe von Logikgattern durchzuführen.
Schauen wir uns zunächst die Addition einzelner Bits an.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
Dies sind die kleinstmöglichen Einzelbitkombinationen. Aber das Ergebnis für 1+1 ist 10. Dieses Problem kann zwar mit Hilfe eines EXOR-Gatters gelöst werden, aber wenn man sich für die Ausgabe interessiert, muss das Summenergebnis als 2-Bit-Ausgabe umgeschrieben werden.
Die obigen Gleichungen können also geschrieben werden als
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
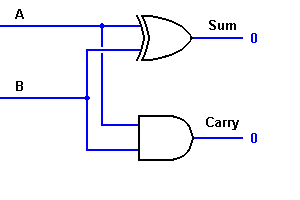
Hier wird die Ausgabe ‚1‘von ’10‘ zum Übertrag. Das Ergebnis ist in einer Wahrheitstabelle unten dargestellt. SUM“ ist der normale Ausgang und „CARRY“ ist der Übertrag.
EINGABEN AUSGABEN
A B SUMME ÜBERTRAG
0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Aus der Gleichung, wird deutlich, dass dieser 1-Bit-Addierer mit Hilfe eines EXOR-Gatters für den Ausgang „SUM“ und eines AND-Gatters für den Übertrag leicht implementiert werden kann. Werfen Sie einen Blick auf die untenstehende Implementierung.
Bei komplexen Additionen kann es vorkommen, dass man zwei 8-Bit-Bytes zusammenzählen muss. Dies kann nur mit Hilfe der Volladdiererlogik geschehen.
Volladdierer
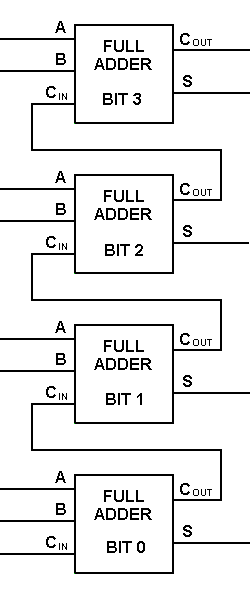
Diese Art von Addierer ist etwas schwieriger zu implementieren als ein Halbaddierer. Der Hauptunterschied zwischen einem Halbaddierer und einem Volladdierer ist, dass der Volladdierer drei Eingänge und zwei Ausgänge hat. Die ersten beiden Eingänge sind A und B und der dritte Eingang ist ein Eingangsübertrag, der als CIN bezeichnet wird. Wenn eine Volladdiererlogik entworfen wird, können wir acht von ihnen aneinanderreihen, um einen byteweiten Addierer zu schaffen und das Übertragsbit von einem Addierer zum nächsten zu kaskadieren.
Der Ausgangsübertrag wird als COUT bezeichnet und der normale Ausgang als S. Sehen Sie sich die Wahrheitstabelle an.
EINGÄNGE AUSGÄNGE
A B CIN COUT S
0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
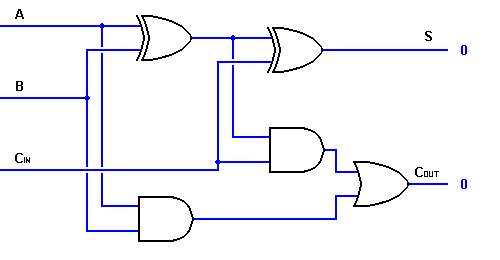
Aus der obigen Wahrheits-Tabelle, kann die Volladdiererlogik implementiert werden. Wir sehen, dass der Ausgang S eine EXOR-Verknüpfung zwischen dem Eingang A und dem Ausgang des Halbaddierers SUM mit den Eingängen B und CIN ist. Wir müssen auch beachten, dass die ZÄHLUNG nur dann wahr ist, wenn einer der beiden Eingänge HIGH ist.
Auf diese Weise können wir eine Volladdierer-Schaltung mit Hilfe von zwei Halbaddierer-Schaltungen implementieren. Der erste Halbaddierer wird verwendet, um A und B zu addieren und eine Teilsumme zu bilden. Die zweite Halbaddiererlogik kann verwendet werden, um CIN zu der vom ersten Halbaddierer erzeugten Summe zu addieren, um die endgültige Ausgabe S zu erhalten. Wenn eine der Halbaddiererlogiken einen Übertrag erzeugt, gibt es einen Ausgangsübertrag. COUT ist also eine ODER-Funktion der Carry-Ausgänge des Halbaddierers. Werfen Sie einen Blick auf die unten gezeigte Implementierung der Volladdierer-Schaltung.
Obwohl die Implementierung größerer Logikdiagramme mit der obigen Volladdierer-Logik möglich ist, wird meist ein einfacheres Symbol zur Darstellung der Operation verwendet. Nachfolgend eine einfachere schematische Darstellung eines Ein-Bit-Volladdierers.
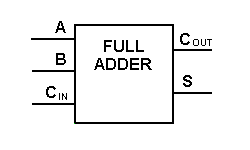
Mit dieser Art von Symbol können wir zwei Bits addieren, indem wir einen Übertrag von der nächst niedrigeren Größenordnung nehmen und einen Übertrag an die nächst höhere Größenordnung senden. In einem Computer muss bei einer Multibit-Operation jedes Bit durch einen Volladdierer dargestellt und gleichzeitig addiert werden. Um zwei 8-Bit-Zahlen zu addieren, werden also 8 Volladdierer benötigt, die durch Kaskadierung von zwei 4-Bit-Blöcken gebildet werden können. Die Addition von zwei 4-Bit-Zahlen ist unten dargestellt.