Los distintos tipos de controladores se utilizan para mejorar el rendimiento de los sistemas de control. En este capítulo, discutiremos los controladores básicos como el proporcional, el derivado y el integral.
Controlador proporcional
El controlador proporcional produce una salida, que es proporcional a la señal de error.
$$u(t) \propto e(t) $$
$$ Flecha derecha u(t)=K_P e(t)$$
Aplique la transformada de Laplace en ambos lados –
$$U(s)=K_P E(s)$$
$$\frac{U(s)}{E(s)}=K_P$$
Por tanto la función de transferencia del controlador proporcional es $K_P$.
Donde,
U(s) es la transformada de Laplace de la señal de actuación u(t)
E(s) es la transformada de Laplace de la señal de error e(t)
KP es la constante de proporcionalidad
El diagrama de bloques del sistema de control de lazo cerrado de retroalimentación negativa unitaria junto con el controlador proporcional se muestra en la siguiente figura.
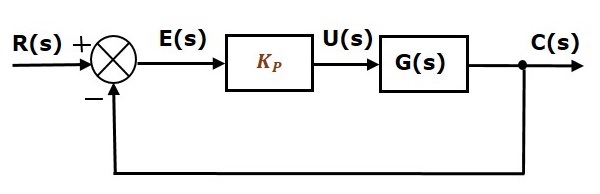
El controlador proporcional se utiliza para cambiar la respuesta transitoria según el requisito.
Controlador derivativo
El controlador derivativo produce una salida, que es derivada de la señal de error.
$$u(t)=K_D \frac{text{d}e(t)}{text{d}t}$$
Aplique la transformada de Laplace en ambos lados.
$$U(s)=K_D sE(s)$$
$$\frac{U(s)}{E(s)}=K_D s$$
Por tanto, la función de transferencia del controlador de la derivada es $K_D s$.
Donde, $K_D$ es la constante de la derivada.
El diagrama de bloques del sistema de control de lazo cerrado de retroalimentación negativa unitaria junto con el controlador de la derivada se muestra en la siguiente figura.
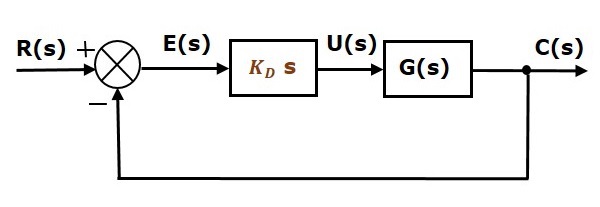
El controlador derivado se utiliza para convertir el sistema de control inestable en uno estable.
Controlador integral
El controlador integral produce una salida, que es integral de la señal de error.
$$u(t)=K_I \int e(t) dt$$
Aplicar la transformada de Laplace en ambos lados –
$U(s)=\frac{K_I E(s)}{s}$$
$$\frac{U(s)}{E(s)}=\frac{K_I}{s}$
Por tanto, la función de transferencia del controlador integral es $\frac{K_I}{s}$.
Donde, $K_I$ es la constante integral.
El diagrama de bloques del sistema de control de lazo cerrado de retroalimentación negativa unitaria junto con el controlador integral se muestra en la siguiente figura.
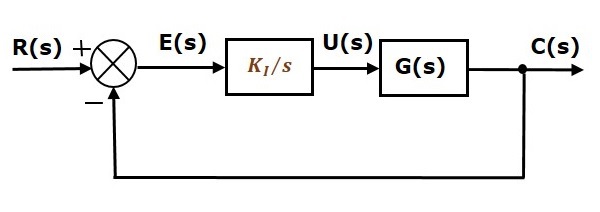
El controlador integral se utiliza para disminuir el error de estado estacionario.
Discutiremos ahora sobre la combinación de controladores básicos.
Controlador proporcional derivativo (PD)
El controlador proporcional derivativo produce una salida, que es la combinación de las salidas de los controladores proporcional y derivativo.
$$u(t)=K_P e(t)+K_D \frac{text{d}e(t)}{text{d}t}$$
Aplique la transformada de Laplace en ambos lados –
$$U(s)=(K_P+K_D s)E(s)$$
$$\frac{U(s)}{E(s)}=K_P+K_D s$$
Por tanto la función de transferencia del controlador proporcional derivativo es $K_P + K_D s$.
El diagrama de bloques del sistema de control de lazo cerrado de retroalimentación negativa unitaria junto con el controlador de derivada proporcional se muestra en la siguiente figura.
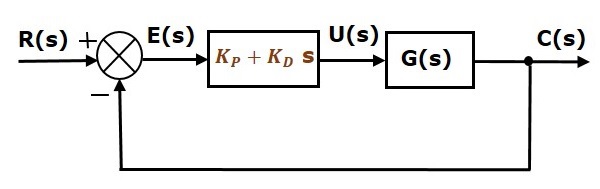
El controlador proporcional derivado se utiliza para mejorar la estabilidad del sistema de control sin afectar al error de estado estacionario.
Controlador proporcional integral (PI)
El controlador proporcional integral produce una salida, que es la combinación de las salidas de los controladores proporcional e integral.
$$u(t)=K_P e(t)+K_I \int e(t) dt$$
Aplique la transformada de Laplace en ambos lados –
$$U(s)=\a la izquierda(K_P+\frac{K_I}{s}\a la derecha )E(s)$$
$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$$
Por lo tanto, la función de transferencia del controlador integral proporcional es $K_P + \frac{K_I} {s}$.
El diagrama de bloques del sistema de control de lazo cerrado de retroalimentación negativa unitaria junto con el controlador integral proporcional se muestra en la siguiente figura.
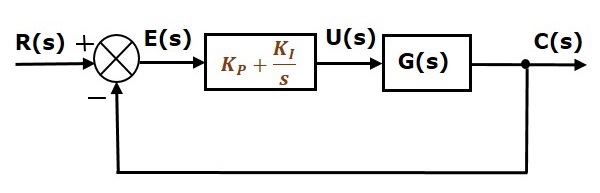
El controlador integral proporcional se utiliza para disminuir el error de estado estacionario sin afectar la estabilidad del sistema de control.
Controlador integral proporcional derivativo (PID)
El controlador integral proporcional derivativo produce una salida, que es la combinación de las salidas de los controladores proporcional, integral y derivativo.
$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{texto{d}e(t)}{texto{d}t}$
Aplique la transformada de Laplace en ambos lados –
$$U(s)=\a la izquierda(K_P+\frac{K_I}{s}+K_D s\a la derecha )E(s)$$
$$frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$
Por lo tanto, la función de transferencia del controlador proporcional integral derivativo es $K_P + \frac{K_I} {s} + K_D s$.
El diagrama de bloques del sistema de control de lazo cerrado de retroalimentación negativa unitaria junto con el controlador proporcional integral derivativo se muestra en la siguiente figura.
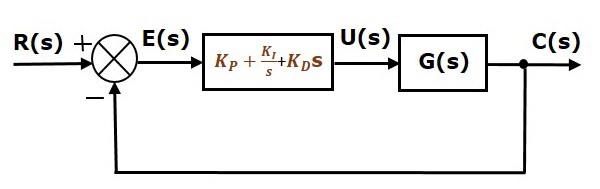
El controlador proporcional integral derivativo se utiliza para mejorar la estabilidad del sistema de control y para disminuir el error de estado estacionario.
.