Una pregunta importante es, ¿cómo se distribuyen los números primos entre los enteros? La respuesta es, en muy pocas palabras, bastante aleatoria, dada cierta estadística básica…
 Bill Casselman
Bill Casselman
Universidad de Columbia Británica, Vancouver, Canadá
Correo electrónico Bill Casselman
| |
|
Introducción
Hace muchos años se conjeturó que hay un número infinito de pares de números primos $p$, $q$ con $q = p+2$. Ha habido algunos avances recientes (y famosos) en este problema. Hablaré poco de los avances recientes, y hablaré en cambio de lo que esperamos -más que de lo que sabemos- sobre tales pares. Nada de lo que diré es nuevo, y hasta cierto punto me he limitado a elaborar lo que Andrew Granville dice en su reciente nota expositiva sobre los avances recientes.
¿Cuántos primos esperamos?
Un número primo es un entero positivo que no tiene divisores excepto él mismo y $1$. La definición es sencilla, pero en cuanto uno empieza a explorar el significado de los números primos se da cuenta de que exhiben un comportamiento mucho más sutil. Una pregunta importante es: ¿cómo se distribuyen los números primos entre los enteros? La respuesta es, en muy pocas palabras, bastante aleatoria, dada cierta estadística básica. ¿Qué quiero decir con esto?
Bien, aquí hay una matriz cuadrada que representa todos los primos hasta $400$:

Hay algunos patrones en esta matriz, algunos de los cuales comentaré más adelante. La mayoría de los que percibes son causados por algún artefacto de la pantalla. Por ejemplo, una de cada dos columnas está esencialmente vacía, y esto se debe a que el único primo par es $2$. Además, una de cada cinco columnas está esencialmente vacía. Más interesantes son los pares de primos gemelos (algunos de los cuales no son tan visibles porque se dividen en dos filas, como $59$, $61$), y también algunos patrones relacionados con los últimos dígitos mostrados. Se trata de lo que podríamos llamar patrones locales. No hay ninguno global aparente.
Se han hecho muchos esfuerzos para conseguir formas extremadamente eficientes de producir números primos, pero hoy en día incluso un programa muy sencillo tarda poco tiempo en hacer grandes listas de primos. Uno de los programas más fructíferos hará una gran lista de números primos y luego usará esto para calcular la función $\pi(n)$, el número de números primos $\le n$.
Una cosa para la que se puede usar esto es para tener una idea aproximada de la frecuencia de los números primos. Hay $135$ primos en el rango $$:
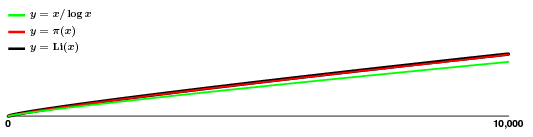
¡La aproximación se ve muy bien! Así que, aunque $\pi(x)$ rebote un poco, aparentemente sin mucho patrón, tenemos una estimación bastante buena para ella, lo que significa que tenemos una buena idea de cómo crecen los primos, al menos en la media.
Hay que tener en cuenta, sin embargo, que la aparente suavidad es engañosa. De cerca, así es como se ven las dos curvas superiores:

¿Comentarios?
Razonamientoeurístico sobre los primos gemelos
Los primos gemelos son un par $p$, $p+2$ que son ambos primos. Por ejemplo, en uno de los gráficos anteriores vemos los primos gemelos $$ , , , , $$
y otros. Se ha conjeturado que hay un número infinito de ellos, pero aunque hay muchas pruebas empíricas de ello aún no se ha demostrado.
Tal vez la prueba más fuerte es una fórmula que aproxima el número $\pi_{2}(x)$ de primos gemelos $\le x$ notablemente bien. No estoy muy seguro del origen de esta fórmula, pero apareció por primera vez en un artículo de G. H. Hardy y J. E. Littlewood (ellos mismos un par de primos gemelos) fechado en 1923. El documento contiene varias fórmulas similares, todas basadas en el mismo método, que habían utilizado para atacar muchos problemas anteriormente. Este era su método del círculo. Su derivación de la fórmula para $\pi_{2}(x)$ no es en absoluto rigurosa, pero es muy convincente. Hay un relato sucinto de esto en un apéndice del artículo de Andrew Granville.
Pero justo después de la Segunda Guerra Mundial Lord Cherwell (Frederick Lindemann) sugirió una derivación probabilística más elemental (y todavía no rigurosa). Esto llevó a una colaboración con E. M. Wright y finalmente a una publicación conjunta póstuma. Esto se explica en la sección 22.20 del conocido texto de Hardy y Wright. También se puede encontrar una versión algo más elemental de esto en un apéndice del artículo de Granville (Sección 2.5). Le sigo.
El punto de partida del razonamiento plausible es nuestra estimación para $\pi(x)$, el número de primos menores o iguales a $x$. La idea básica de la derivación es que los números primos están, en buena medida, distribuidos aleatoriamente. Sabemos que en la vecindad de $x$ la densidad de los primos es aproximadamente $1/\log x$. Si los números primos estuvieran distribuidos aleatoriamente, entonces la probabilidad de que dos números dados cerca de $x$ sean primos sería simplemente el producto de las probabilidades locales, que es $1/\log^{2} x$. Esto es ciertamente un razonamiento engañoso, ya que si $n > 2$ la probabilidad de que tanto $n$ como $n+1$ sean primos es $0$, mientras que el hecho de que $p$ sea un primo parecería aumentar las posibilidades de que $p+2$ lo sea. Hay consideraciones similares a tener en cuenta debido a la posible divisibilidad por otros primos pequeños, también, en la vecindad de $x$.
Hay un hecho simple en esta historia. Si $q$ es cualquier primo, entonces la probabilidad de elegir un entero al azar que no sea divisible por $q$ es $1-1/q$. La probabilidad de elegir dos que no sean divisibles por $q$ es, por tanto, el producto $(1 – 1/q)^{2}$. Supongamos que $p$ y $p+2$ son ambos primos, entonces ni $p$ ni $p+2$ son divisibles por $q$. Si $q = 2$, esto ocurre 1/2$ de las veces. Si $q \N es 2$, la probabilidad de que $p \N no sea igual a 0$ y $p \N no sea igual a -2$ \N en el módulo $q$ es $(1 – 2/q)$. Debido al Teorema del Resto Chino, la divisibilidad por dos primos es un evento independiente. Así que si $x$ es grande y $Q$ es relativamente pequeño, la probabilidad de que cualquier par de números $m$ y $n$ cerca de $x$ no sea múltiplo de ningún primo hasta $Q$ es $$ { 1\sobre 2} \cdot \d_{q \le Q} { (1 – 1/q)^{2} } \. $$
Sea $\Gamma_{Q}$ el cociente de esto a $\prod_{q \le Q}(1 – 2/q)$: $$ \Gamma_{Q} = { 1\ sobre 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \sobre (1 – 2/q) } $$ Tenemos $$ { 1 – 2/q \\\Nsobre (1-1/q)^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \sobre (1 – 1/q)^{2} } } = 1 – { 1 \\Nsobre (q -1)^{2} } \N – . $$ Un criterio estándar afirma que este producto converge si la suma $\Nsum 1/(q-1)^{2}$ converge. Pero sí converge ya que la prueba integral nos dice que $\suma 1/n^{2}$ converge. Por lo tanto este producto realmente converge a un número $\Pi_{infty}$ como $Q \rightarrow \infty$. Sea $C_{2}$ su inversa. La sección 2.5 del artículo de Granville dice que debería ser intuitivamente razonable en este punto que el número $\pi_{2}(x)$ de primos gemelos $\le x$ se aproxima por $$ \Pi_{2}(x) = C_{2} \int_{2}^{infty} { dx \ sobre \log^{2} x } \N – $$
El texto de Hardy y Wright establece un análisis más cuidadoso que hace que el salto intuitivo sea un poco más claro.
El valor de la constante aquí fue calculado hace mucho tiempo por J. W. Wrench para ser alrededor de $1.320323631693739147855624002911155686525 \ldots $. He aquí una comparación de algunos valores de $\pi_{2}(x)$ y la fórmula en el rango $$: $$ \matrix{ n & 10.000 & 20.000 & 30.000 & 40.000 & 50.000 \cr \pi_{2}(n) & 205\phantom{.0} & 342 fantasmas.
¿Comentarios?
La conjetura de Dickson
Los primos gemelos son un caso especial de algo mucho más general. Uno puede preguntarse, ¿hay un número infinito de pares $p$, $p+4$ o $p$, $p+6$ que sean primos? ¿O $p$, $p+10$? El caso de $p$ y $p+10$ está ciertamente sugerido por una de las imágenes de arriba, en la que tales pares son fácilmente visibles. ¿Qué hay de los triples de algún tipo? Supongamos que $a_{1}$, $a_{2}$, $\ldots$ , $a_{k}$ forman una matriz de enteros. ¿Podemos esperar que haya un número infinito de conjuntos $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$ que sean todos primos?
Hay que tener un poco de cuidado. No hay pares primos de la forma $p$, $p+1$ (pasado $p = 2$), porque uno de estos dos números debe ser divisible por $2$. Del mismo modo, más allá de $p = 3$ no hay triples primos $p$, $p+2$, $p+4$ porque uno de ellos debe ser divisible por $3$.
Este último ejemplo debería ser ilustrativo. El número $p+4$ es divisible por $3$ si y sólo si $p+1$ es divisible por $3$. Por tanto, $3$ divide a uno de los números $p$, $p+2$, $p+4$ si y sólo si divide a $p$, $p+1$, $p+2$. Pero esto es seguro, ya que el último triple cubre claramente todos los números módulo $3$.
En general, se dice que $p$ es un obstáculo para la matriz $(a_{i})$ si $p$ siempre divide al menos uno de cada secuencia $n+a_{i}$ ($i = 1$, $\ldots$, $k$). Esto ocurre si y sólo si los números $a_{i} \N – mod mod} \N, p$ llenan todo $Z/p$.
Esto nunca puede ocurrir si $p > k$, por lo que para comprobar si algún $p$ obstruye $(a_{i})$ sólo tenemos que comprobar si los $a_{i}$ cubren $Z/p$ para todo $p \Nk$. Llamamos admisible a la matriz $(a_{i})$ si no tiene obstáculos primos.
Por ejemplo, $(1,3,7,9)$ es una matriz admisible, ya que, como se puede comprobar fácilmente, ni $2$ ni $3$ son obstáculos. En uno de los diagramas anteriores se pueden ver varias secuencias de primos que se ajustan a este patrón. Otros ejemplos son (a) cualquier $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
Existen conjuntos admisibles arbitrariamente grandes. De hecho:
Teorema. Si de $a_{1}$ a $a_{k}$ es cualquier conjunto de primos distintos $> k$, constituyen un conjunto admisible.
¿Por qué? Si $p$ es cualquier primo en el que $p> k$, entonces ya hemos visto que no puede ser una obstrucción. Pero si $p \le k$, entonces no puede dividir a ninguno de los $a_{i}$, ninguno de los cuales puede ser congruente con $0$ módulo $p$. Así que los $a_{i}$ no llenan $Z/p$.
Un caso especial de una conjetura hecha originalmente por L. E. Dickson es que si no hay obstáculos primos para $(a_{i})$ entonces existe un número infinito de secuencias primas de la forma $(n +a_{i})$.
Lo que ha sucedido recientemente
Este no es el lugar para contar toda la historia, que ha sido cubierta a fondo en otros lugares. Recomiendo especialmente el artículo de Quanta de Erica Klarreich para un relato popular, y el ensayo de Granville para uno más técnico. Sólo quiero exponer con un poco más de precisión que en el relato de Klarreich cuál es el más famoso de los nuevos resultados.
Se debe a Yitang Zhang. El enunciado más simple de lo que demostró es que existe un número infinito de intervalos $[n, n+70.000.000)$ que contienen al menos dos primos. Esto es más débil que la conjetura de los primos gemelos, pero conceptualmente está muy cerca de ella. En trabajos posteriores (realizados por muchos matemáticos) se ha reducido mucho el tamaño de la brecha, pero presumiblemente no hay forma de reducirla a $2$ con los métodos actuales.
Como explica Granville, el primer resultado de Zhang, y podría decirse que el principal, es que existe $k$ con la propiedad de que si $a_{1}$, $\ldots$ , $a_{k}$ es un conjunto admisible de $k$ elementos, entonces existe un número infinito de $n$ tal que $\{ n +a_{i} \contiene al menos dos primos. (En el artículo de Klarreich sobre Quanta, el conjunto se llama «peine». Hay que tener en cuenta que, según la conjetura de Dickson, esperaríamos poder decir que todos los $k$ son primos). De hecho, Zhang demostró que esta afirmación es cierta para un $k =3.500.000$ particular que abarca un intervalo de $70.000.000$. La ya famosa consecuencia es que para algún $m \lt 70.000.000$ existe un número infinito de pares primos $p$, $p+m$.
Leyendo más
- Lord Cherwell y E. M. Wright, «The frequency of prime patterns», The Quarterly Journal of Mathematics 11 (1960).
Aquellos que conozcan algo de la vida de Lord Cherwell, también conocido como Frederick Lindemann, se sorprenderán mucho al conocer su contribución a la teoría de números. La biografía de Wikipedia no sugiere adecuadamente todas las razones de su mala reputación como principal asesor científico de Churchill durante la Segunda Guerra Mundial.
- L. E. Dickson, «A new extension of Dirichlet’s theorem on prime numbers», Messenger of Mathematics 33.
Véase también la entrada de Wikipedia sobre la conjetura de Dickson.
- Andrew Granville, «Primes in intervals of bounded length». Disponible en su página web.
- G. H. Hardy, Ramanujan, Cambridge University Press.
La sección 2.5 contiene una derivación ideal de una posible fórmula para $\pi(x)$.
- G. H. Hardy y J. E. Littlewood, «Some problems of ‘Partitio numerorum’ III: on the expression of a number as a sum of primes», Acta Mathematica 44 (1923).
- G. H. Hardy y E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, «Together and alone, closing the prime gap», Quanta 19 de noviembre de 2013.
- B. Riemann, «Sobre el número de números primos menores que una cantidad dada». Una traducción al inglés de este clásico realizada por David Wilkins está disponible en un enlace de Wikipedia.
Entre otras cosas, se esboza una derivación de la fórmula aproximada de $\pi(x)$.
- J. W. Wrench, «Evaluation of Artin’s constant and the twin-prime constant», Mathematics of Computation 76 (1961).
Un primer cálculo de $C_{2}$.
- Listas de primos hasta 1.000.000.000$
- Una lista de los primeros 20.000 primos gemelos.
 Bill Casselman
Bill Casselman
Universidad de la Columbia Británica, Vancouver, Canadá
Email Bill Casselman