- Objetivos de aprendizaje
- Función a trozos
- Evaluar una función definida a trozos
- Ejemplo
- Ejemplo
- Escribir una función definida a trozos
- Ejemplo
- Dada una función a trozos, escribe la fórmula e identifica el dominio de cada intervalo.
- Graficar funciones a trozos
- Dada una función a trozos, dibuje una gráfica.
- Ejemplo
- Ejemplo
- Resumen
Objetivos de aprendizaje
- Introducción a las funciones a trozos
- Definir una función a trozos función
- Evaluar una función a trozos
- Escribir una función a trozos dada una aplicación
- Graficar funciones a trozos
- Dada una función a trozosfunción definida a trozos, dibujar una gráfica
- Escribir el dominio y el rango de una función a trozos dada una gráfica
Algunas funciones vienen a trozos. En esta sección, aprenderemos a definir y graficar funciones que son esencialmente colecciones de piezas discretas. Ejemplos de algo definido de esta manera incluyen el diseño del perfil de un coche, el cálculo de su plan de teléfono móvil, y el cálculo de las tasas de impuestos sobre la renta. Por ejemplo, su tasa de impuestos depende de sus ingresos y es la misma para un rango de ingresos, como se muestra en la siguiente tabla:
| Tipo impositivo marginal | Renta imponible de soltero | Casado que declara conjuntamente o viudo cualificado Ingresos | Casado que declara por separado Ingresos imponibles | Ingresos imponibles del jefe de familia |
|---|---|---|---|---|
| 10% | $0 – $9,275 | $0 – $18,550 | $0 – $9,275 | $0 – $13,250 |
| 15% | $9,276 – $37,650 | $18,551 – $75,300 | $9,276 – $37,650 | $13,251 – $50,400 |
| 25% | $37,651 – $91,150 | $75,301 – $151,900 | $37,651 – $75,950 | $50,401 – $130,150 |
| 28% | $91,151 – $190,150 | $151,901 – $231,450 | $75,951 – $115,725 | $130,151 – $210,800 |
| 33% | $190,151 – $413,350 | $231,451 – $413,350 | $115,726 – $206,675 | $210,801 – $413,350 |
| 35% | $413,351 – $415,050 | $413,351 – $466,950 | $206,676 – $233,475 | $413,351 – $441,000 |
| 39.6% | $415,051+ | $466,951+ | $233,476+ | $441,001+ |
Una función a trozos es una función en la que se utiliza más de una fórmula para definir la salida sobre diferentes trozos del dominio.
Usamos las funciones a trozos para describir situaciones en las que una regla o relación cambia cuando el valor de entrada cruza ciertos «límites». Por ejemplo, a menudo nos encontramos con situaciones en los negocios para las que el coste por pieza de un determinado artículo se descuenta una vez que el número pedido supera un determinado valor. Los tramos de impuestos son otro ejemplo del mundo real de funciones a trozos. Por ejemplo, consideremos un sistema fiscal simple en el que los ingresos hasta 10.000 dólares se gravan al 10%, y cualquier ingreso adicional se grava al 20%. El impuesto sobre un ingreso total, S, sería 0,1S si S\le 10.000 dólares y 1000 + 0,2 (S – 10.000 dólares), si S> 10.000 dólares.
Función a trozos
Una función a trozos es una función en la que se utiliza más de una fórmula para definir el resultado. Cada fórmula tiene su propio dominio, y el dominio de la función es la unión de todos estos dominios más pequeños. Anotamos esta idea así:
f\a izquierda(x\a derecha)=\año{cuestiones} {texto{fórmula 1 si x está en el dominio 1} {texto{fórmula 2 si x está en el dominio 2} {texto{fórmula 3 si x está en el dominio 3} {casos}
En notación a trozos, la función de valor absoluto es
Evaluar una función definida a trozos
En el primer ejemplo, mostraremos cómo evaluar una función definida a trozos. Observe cómo es importante prestar atención al dominio para determinar qué expresión utilizar para evaluar la entrada.
Ejemplo
Dada la función
f(x)=\comenzar{casos}7x+3{texto} si }x<0\comenzar{casos}+6{texto},
evaluar:
- f (-1)
- f (0)
- f (2)
En el siguiente vídeo mostramos cómo evaluar varios valores dada una función definida a trozos.
En el siguiente ejemplo mostramos cómo evaluar una función que modela el coste de la transferencia de datos para una compañía telefónica.
Ejemplo
Una compañía de telefonía móvil utiliza la siguiente función para determinar el coste, C, en dólares para g gigabytes de transferencia de datos.
Hallar el costo de usar 1.5 gigabytes de datos y el coste de usar 4 gigabytes de datos.
Análisis de la solución
La función se representa en el gráfico siguiente. Podemos ver donde la función cambia de una constante a una línea con pendiente positiva en g=2. Trazamos las gráficas de las diferentes fórmulas en un conjunto común de ejes, asegurándonos de que cada fórmula se aplica en su propio dominio.

C(g) = C\a la izquierda(g\a la derecha)=\a la entrada{casos}{25}{texto} si{ 0}<{ g}<{ 2}{ 10g+5}{texto} si{ g}{ 2}{fin{casos}
Escribir una función definida a trozos
En el último ejemplo mostraremos cómo escribir una función definida a trozos que modele el precio de una visita guiada a un museo.
Ejemplo
Un museo cobra 5 dólares por persona por una visita guiada con un grupo de 1 a 9 personas o una tarifa fija de 50 dólares para un grupo de 10 o más personas. Escriba una función que relacione el número de personas, n, con el coste, C.
Análisis de la solución
La función se representa en la figura 21. La gráfica es una línea diagonal desde n=0 hasta n=10 y una constante después. En este ejemplo, las dos fórmulas coinciden en el punto de encuentro donde n=10, pero no todas las funciones a trozos tienen esta propiedad.

En el siguiente vídeo mostramos un ejemplo de escritura de una función definida a trozos dado un escenario.
Dada una función a trozos, escribe la fórmula e identifica el dominio de cada intervalo.
- Identificar los intervalos para los que se aplican diferentes reglas.
- Determinar fórmulas que describan cómo calcular una salida a partir de una entrada en cada intervalo.
- Utilizar llaves y sentencias if para escribir la función.
Graficar funciones a trozos
En esta sección, graficaremos funciones a trozos. La función trazada a continuación representa el coste de transferencia de datos para una determinada compañía de telefonía móvil. Podemos ver donde la función cambia de una constante a una línea con una pendiente positiva en g=2. Cuando trazamos funciones a trozos, es importante asegurarse de que cada fórmula se aplica en su propio dominio. \text{ si }{ 0 }<{ g }<{ 2 }\10g+5\text{ si }{ g}\ge{ 2 }\end{cases}
En este caso, la salida es 25 para cualquier entrada entre 0 y 2. Para valores iguales o mayores que 2, la salida se define como 10g+5.

Dada una función a trozos, dibuje una gráfica.
- Indique en el eje x los límites definidos por los intervalos en cada trozo del dominio.
- Para cada trozo del dominio, grafique en ese intervalo usando la ecuación correspondiente perteneciente a ese trozo. No grafique dos funciones sobre un intervalo porque violaría el criterio de una función.
Ejemplo
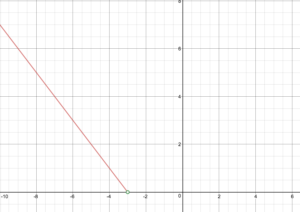
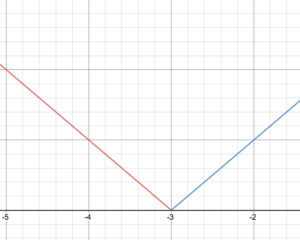
Esquema una gráfica de la función.
Dada la definición a trozos de f(x)=comienza-x – 3\text{ si}x < -3\ x + 3\text{ si} x \ge -3\cases}
Dibuja la gráfica de f.
Indicar el dominio y el rango de la función.
En el siguiente ejemplo, graficaremos una función definida a trozos que modela el costo de envío de una tienda de cómics en línea.
Ejemplo
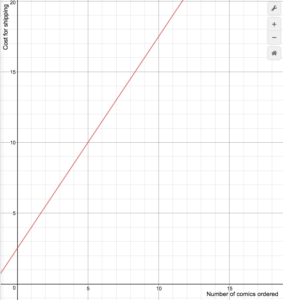
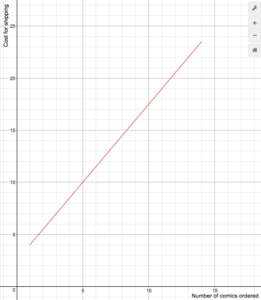
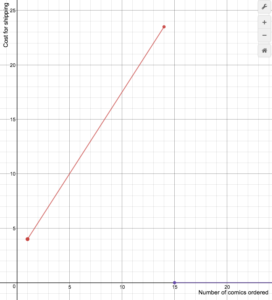
Un minorista de cómics en línea cobra los costes de envío de acuerdo con la siguiente fórmula
S(n)={comenzar}1,5n+2.5\texto{si}1\le{n}\le14\\\0\texto{si}n\ge15\final{cases}
Dibuja una gráfica de la función de costes.
En el siguiente vídeo mostramos cómo graficar una función definida a trozos que es lineal sobre ambos dominios.
Resumen
- Una función a trozos es una función en la que se utiliza más de una fórmula para definir la salida sobre diferentes trozos del dominio.
- Evaluar una función a trozos significa que hay que prestar mucha atención a la expresión correcta utilizada para la entrada dada
Para graficar funciones a trozos, primero hay que identificar dónde se divide el dominio. Grafique las funciones en el dominio usando herramientas como puntos de trazado, o transformaciones. Tenga cuidado de usar círculos abiertos o cerrados en los puntos finales de cada dominio en función de si el punto final está incluido.