Circuito de Media Suma y Suma Completa
Los circuitos de Media Suma y Suma Completa se explican con sus tablas de verdad en este artículo. También se muestra el diseño del Sumador Completo utilizando el circuito del Medio Sumador. También se muestra el circuito Full Adder de un solo bit y la adición de varios bits utilizando Full Adder.
Antes de entrar en este tema, es muy importante conocer la lógica booleana y las puertas lógicas.
Mira: Lógica Booleana
Mira: Puertas Lógicas
Mira: FLIP FLOPS
¿Qué es un Sumador?
Un sumador es un tipo de calculadora que se utiliza para sumar dos números binarios. Cuando digo, calculadora, no me refiero a una con botones, esta es un circuito que se puede integrar con muchos otros circuitos para una amplia gama de aplicaciones. Existen dos tipos de sumadores;
- Medio sumador
- Sumador completo
Medio sumador
Con la ayuda del medio sumador, podemos diseñar circuitos capaces de realizar sumas simples con la ayuda de puertas lógicas.
Veamos primero la suma de bits simples.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
Estas son las menores combinaciones posibles de bits simples. Pero el resultado de 1+1 es 10. Aunque este problema puede ser resuelto con la ayuda de una puerta EXOR, si te importa la salida, el resultado de la suma debe ser reescrito como una salida de 2 bits.
Así, las ecuaciones anteriores se pueden escribir como
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Aquí la salida ‘1’de ’10’ se convierte en el carry-out. El resultado se muestra en una tabla de verdad a continuación. ‘SUM’ es la salida normal y ‘CARRY’ es el carry-out.
Salidas
A B SUM CARRY
0 0 0
0 1 1 0
1 0 1 0
1 0 1
De la ecuación, está claro que este sumador de 1 bit puede ser fácilmente implementado con la ayuda de la compuerta EXOR para la salida ‘SUM’ y una compuerta AND para el acarreo. Echa un vistazo a la implementación de abajo.
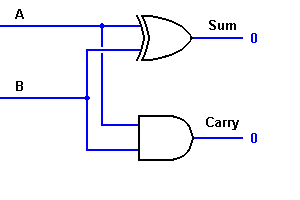
Para la adición compleja, puede haber casos en los que tienes que sumar dos bytes de 8 bits. Esto se puede hacer sólo con la ayuda de la lógica de la escalera completa.
Sumador completo
Este tipo de sumador es un poco más difícil de implementar que una media escalera. La principal diferencia entre una media escalera y una escalera completa es que la escalera completa tiene tres entradas y dos salidas. Las dos primeras entradas son A y B y la tercera entrada es un acarreo de entrada designado como CIN. Cuando se diseñe una lógica de sumador completo podremos encadenar ocho de ellos para crear un sumador de ancho de byte y conectar en cascada el bit de acarreo de un sumador al siguiente.
El acarreo de salida se designa como COUT y la salida normal se designa como S. Eche un vistazo a la tabla de verdad.
SALIDAS
A B CIN COUT S
0 0 0 0
0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 1
1 0 1 0
1 1 0 1 0
1 1 1 1
De la tabla de verdad anterior-tabla, se puede implementar la lógica del sumador completo. Podemos ver que la salida S es un EXOR entre la entrada A y la salida de la media suma con las entradas B y CIN. También debemos tener en cuenta que el COUT sólo será verdadero si alguna de las dos entradas de las tres es ALTA.
Así, podemos implementar un circuito sumador completo con la ayuda de dos circuitos semi sumadores. El primer medio sumador se utilizará para sumar A y B para producir una suma parcial. La lógica del segundo medio sumador se puede utilizar para añadir CIN a la suma producida por el primer medio sumador para obtener la salida final S. Si alguna de las lógicas de los semi sumadores produce un acarreo, habrá un acarreo de salida. Por lo tanto, COUT será una función OR de las salidas de acarreo del semi sumador. Eche un vistazo a la implementación del circuito sumador completo que se muestra a continuación.
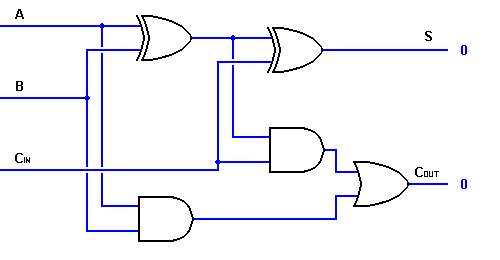
Aunque la implementación de diagramas lógicos más grandes es posible con la lógica del sumador completo anterior, se utiliza principalmente un símbolo más simple para representar la operación. A continuación se muestra una representación esquemática más simple de un sumador completo de un bit.
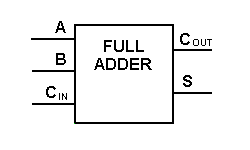
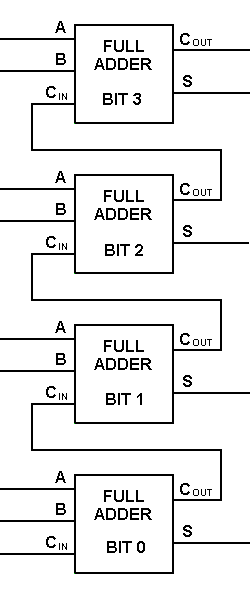
Con este tipo de símbolo, podemos sumar dos bits tomando un acarreo del siguiente orden de magnitud inferior, y enviando un acarreo al siguiente orden de magnitud superior. En un ordenador, para una operación de varios bits, cada bit debe estar representado por un sumador completo y debe sumarse simultáneamente. Así, para sumar dos números de 8 bits, se necesitan 8 sumadores completos que se pueden formar conectando en cascada dos de los bloques de 4 bits. La suma de dos números de 4 bits se muestra a continuación.