Comencemos examinando la división de valores con exponentes.
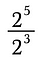
Recordemos que los exponentes representan la multiplicación repetida. Así que podemos reescribir la expresión anterior como:
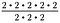
Como 2/2 = 1, cancela tres conjuntos de 2/2. Esto deja 2 – 2, o 2 al cuadrado.
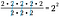
Por supuesto, podemos tomar un atajo y restar el número de 2 de abajo del número de 2 de arriba. Como estas cantidades están representadas por sus respectivos exponentes, lo único que tenemos que hacer es escribir la base común con la diferencia de valores de los exponentes como potencia.
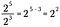
Si generalizamos esta regla, tenemos lo siguiente donde n representa un número real distinto de cero y x e y son también números reales.
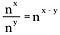
Explorando la potencia cero
A partir de aquí es fácil derivar la explicación de por qué cualquier número distinto de cero elevado a la potencia cero es igual a 1. De nuevo, veamos un ejemplo concreto.
Sabemos que cualquier número distinto de cero dividido por sí mismo es igual a 1. Así que puedo escribir lo siguiente:
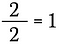
Esto es lo mismo que escribir:
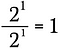
Ahora utilizaré la regla del exponente de arriba para reescribir el lado izquierdo de esta ecuación.
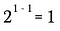
Por supuesto, esto es equivalente a:
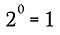
Podemos utilizar el mismo proceso que en este ejemplo, junto con la regla generalizada anterior, para demostrar que cualquier número real distinto de cero elevado a la potencia cero debe dar como resultado 1.
¿Qué pasa con el cero a la potencia cero?
Aquí es donde las cosas se complican. El método anterior se rompe porque, por supuesto, dividir por cero es un no-no. Vamos a examinar por qué.
Empezaremos por ver un ERROR común de división por cero.
¿Qué tal 2÷0? Veamos por qué no podemos hacerlo.
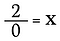
La división es realmente sólo una forma de multiplicación, así que lo que sucede si reescribo la ecuación anterior como:
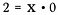
¿Qué valor podría satisfacer esta ecuación para x?
¡No hay ningún valor! Cualquier número multiplicado por cero da como resultado cero, nunca puede ser igual a 2. Por lo tanto, decimos que la división por cero es indefinida. No hay solución posible.
Ahora veamos 0÷0.
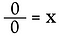
De nuevo, reescríbelo como un problema de multiplicación.
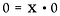
Aquí nos encontramos con una situación muy diferente. La solución para x podría ser CUALQUIER número real. No hay forma de determinar cuál es x. Por lo tanto, 0/0 se considera indeterminado*, no indefinido.
Si intentamos utilizar el método anterior con el cero como base para determinar lo que sería el cero a la potencia cero, nos detenemos inmediatamente y no podemos continuar porque sabemos que 0÷0 ≠ 1, pero es indeterminado.
¿Entonces a qué equivale el cero a la potencia cero?
Esto es muy debatido. Algunos creen que debe definirse como 1, mientras que otros piensan que es 0, y algunos creen que es indefinido. Hay buenos argumentos matemáticos para cada uno de ellos, y quizás lo más correcto es considerarlo indeterminado.
A pesar de esto, la comunidad matemática está a favor de definir el cero a la potencia cero como 1, al menos para la mayoría de los propósitos.
Quizás una definición útil de los exponentes para el matemático aficionado sea la siguiente: