La fórmula estándar para encontrar el determinante de una matriz de 3×3 es una descomposición de problemas de determinantes de 2×2 más pequeños que son muy fáciles de manejar. Si necesitas un repaso, echa un vistazo a mi otra lección sobre cómo encontrar el determinante de un 2×2. Supongamos que nos dan una matriz cuadrada A donde,
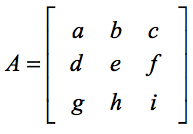
El determinante de la matriz A se calcula como
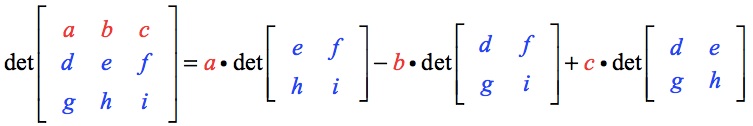
Aquí están los puntos clave:
- Nótese que los elementos de la fila superior, es decir, a, b y c sirven como multiplicadores escalares a una matriz correspondiente de 2 por 2.
- El escalar a se está multiplicando a la matriz 2×2 de elementos sobrantes creada cuando se dibujan segmentos de líneas verticales y horizontales que pasan por a.
- El mismo proceso se aplica para construir las matrices 2×2 para los multiplicadores escalares b y c.
Determinante de la matriz 3×3 (animado)

Ejemplos de cómo hallar el determinante de una matriz 3×3
Ejemplo 1: Encuentra el determinante de la matriz 3×3 que aparece a continuación.
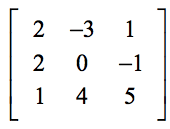
El montaje que aparece a continuación te ayudará a encontrar la correspondencia entre los elementos genéricos de la fórmula y los elementos del problema real.
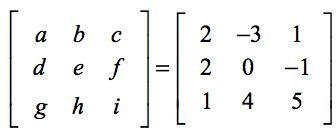
Aplicando la fórmula,


Ejemplo 2: Evaluar el determinante de la matriz de 3×3 que aparece a continuación.
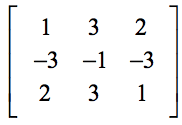
Tenga mucho cuidado al sustituir los valores en los lugares correctos de la fórmula. Los errores más comunes ocurren cuando los estudiantes se descuidan durante el paso inicial de sustitución de valores.
Además, tómate tu tiempo para asegurarte de que tu aritmética también es correcta. De lo contrario, un solo error en alguna parte del cálculo dará una respuesta errónea al final.
Dado que,
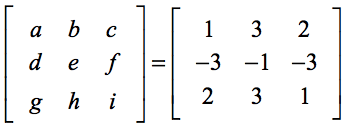
nuestro cálculo del determinante se convierte en…

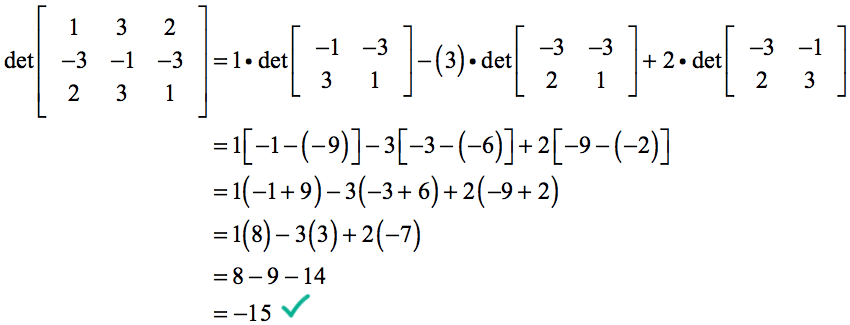
Ejemplo 3: Resuelve el determinante de la matriz de 3×3 de abajo.
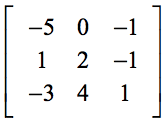
La presencia del cero (0) en la primera fila debería facilitarnos el cálculo. Recuerda que los elementos de la primera fila actúan como multiplicadores escalares. Por lo tanto, el cero multiplicado a cualquier cosa hará que toda la expresión desaparezca.