Física

La fisión nuclear es una reacción en la que un núcleo se divide (o se fisura). La fisión controlada es una realidad, mientras que la fusión controlada es una esperanza para el futuro. Cientos de centrales de fisión nuclear en todo el mundo atestiguan que la fisión controlada es práctica y, al menos a corto plazo, económica, como se ve en la Figura 1. Mientras que la energía nuclear no interesó durante décadas tras TMI y Chernóbil (y ahora Fukushima Daiichi), la creciente preocupación por el calentamiento global ha vuelto a poner la energía nuclear sobre la mesa como una alternativa energética viable. A finales de 2009, había 442 reactores en funcionamiento en 30 países, que proporcionan el 15% de la electricidad mundial. Francia suministra más del 75% de su electricidad con energía nuclear, mientras que Estados Unidos tiene 104 reactores en funcionamiento que proporcionan el 20% de su electricidad. Australia y Nueva Zelanda no tienen ninguno. China está construyendo centrales nucleares a razón de una cada mes.

Figura 1. Las personas que viven cerca de esta central nuclear no tienen una exposición medible a la radiación que se puede rastrear a la planta. Alrededor del 16% de la energía eléctrica mundial se genera mediante fisión nuclear controlada en este tipo de centrales. Las torres de refrigeración son las características más destacadas, pero no son exclusivas de la energía nuclear. El reactor está en el pequeño edificio abovedado a la izquierda de las torres. (crédito: Kalmthouts)

La fisión es lo contrario de la fusión y sólo libera energía cuando los núcleos pesados se dividen. Como se indica en Fusión, se libera energía si los productos de una reacción nuclear tienen una energía de enlace por nucleón (BE/A) mayor que la de los núcleos padres. La figura 2 muestra que la BE/A es mayor para los núcleos de masa media que para los núcleos pesados, lo que implica que cuando un núcleo pesado se divide, los productos tienen menos masa por nucleón, por lo que esa masa se destruye y se libera energía en la reacción. La cantidad de energía por reacción de fisión puede ser grande, incluso para los estándares nucleares. El gráfico de la Figura 2 muestra que BE/A es de unos 7,6 MeV/nucleón para los núcleos más pesados (A alrededor de 240), mientras que BE/A es de unos 8,6 MeV/nucleón para los núcleos que tienen A alrededor de 120. Por tanto, si un núcleo pesado se divide por la mitad, se libera alrededor de 1 MeV por nucleón, o aproximadamente 240 MeV por fisión. Esto es unas 10 veces la energía por reacción de fusión, y unas 100 veces la energía de la desintegración media α, β o γ.

Puede producirse una fisión espontánea, pero normalmente no es el modo de desintegración más común para un determinado nucleido. Por ejemplo, el 238U puede fisionarse espontáneamente, pero decae principalmente por emisión α. La fisión inducida por neutrones es crucial, como se ve en la Figura 2. Al no tener carga, incluso los neutrones de baja energía pueden golpear un núcleo y ser absorbidos una vez que sienten la fuerza nuclear atractiva. Los núcleos grandes se describen mediante un modelo de gota líquida con tensión superficial y modos de oscilación, porque el gran número de nucleones actúa como los átomos de una gota. El neutrón es atraído y, por tanto, deposita energía, haciendo que el núcleo se deforme como una gota líquida. Si se estira lo suficiente, el núcleo se estrecha en el centro. El número de nucleones en contacto y la fuerza nuclear que une el núcleo se reducen. La repulsión de Coulomb entre los dos extremos consigue entonces fisionar el núcleo, que estalla como una gota de agua en dos grandes trozos y unos pocos neutrones. La fisión inducida por neutrones puede escribirse como

n + AX → FF1 + FF2 + xn,

donde FF1 y FF2 son los dos núcleos hijos, llamados fragmentos de fisión, y x es el número de neutrones producidos. La mayoría de las veces, las masas de los fragmentos de fisión no son iguales. La mayor parte de la energía liberada se destina a la energía cinética de los fragmentos de fisión, mientras que el resto se destina a los neutrones y a los estados excitados de los fragmentos. Dado que los neutrones pueden inducir la fisión, es posible que se produzca una reacción en cadena autosostenida, siempre que se produzca más de un neutrón de media, es decir, si x>1 en n + AX → FF1 + FF2 + xn. Esto también puede verse en la figura 3. Un ejemplo de una típica reacción de fisión inducida por neutrones es

n+{}_{texto{92}^{texto{235}{texto{U}}a {}{texto{56}^{texto{142}{texto{Ba}+{}{texto{36}^{texto{91}{texto{Kr}+3{texto{n}}.

Nótese que en esta ecuación, la carga total permanece igual (se conserva): 92 + 0 = 56 + 36. También, en cuanto a los números enteros, la masa es constante: 1 + 235 = 142 + 91 + 3. Esto no es cierto cuando consideramos las masas hasta 6 ó 7 cifras significativas, como en el ejemplo anterior.

Figura 2. Se muestra la fisión inducida por neutrones. En primer lugar, la energía se pone en este gran núcleo cuando absorbe un neutrón. Actuando como una gota de líquido golpeada, el núcleo se deforma y comienza a estrecharse en el centro. Como hay menos nucleones en contacto, la fuerza repulsiva de Coulomb es capaz de romper el núcleo en dos partes y algunos neutrones también salen volando.

Figura 3. Una reacción en cadena puede producir una fisión autosostenida si cada fisión produce suficientes neutrones para inducir al menos una fisión más. Esto depende de varios factores, incluyendo cuántos neutrones se producen en una fisión promedio y cuán fácil es hacer que un tipo particular de nucleido se fisione.

No todos los neutrones producidos por la fisión inducen la fisión. Algunos neutrones escapan del material fisionable, mientras que otros interactúan con un núcleo sin hacerlo fisionar. Podemos aumentar el número de fisiones producidas por los neutrones teniendo una gran cantidad de material fisionable. La cantidad mínima necesaria para la fisión autosostenida de un determinado nucleido se denomina su masa crítica. Algunos nucleidos, como el 239Pu, producen más neutrones por fisión que otros, como el 235U . Además, algunos nucleidos son más fáciles de fisionar que otros. En particular, el 235U y el 239Pu, son más fáciles de fisionar que el mucho más abundante 238U . Ambos factores afectan a la masa crítica, que es más pequeña para el 239Pu.

La razón por la que el 235U y el 239Pu son más fáciles de fisionar que el 238U es que la fuerza nuclear es más atractiva para un número par de neutrones en un núcleo que para un número impar. Consideremos que el {{texto{92}}^{texto{235}} {{texto{143}} tiene 143 neutrones, y el {{texto{94}}^{texto{239}} {{texto{P}} tiene 145 neutrones, mientras que el {{texto{92}}^{texto{238}} {{texto{U}} tiene 146. Cuando un neutrón encuentra un núcleo con un número impar de neutrones, la fuerza nuclear es más atractiva, porque el neutrón adicional hará que el número sea par. En el núcleo resultante se deposita unos 2 MeV más de energía que si el número de neutrones ya fuera par. Esta energía adicional produce una mayor deformación, haciendo más probable la fisión. Así, el 235U y el 239Pu son combustibles de fisión superiores. El isótopo 235U es sólo el 0,72% del uranio natural, mientras que el 238U es el 99,27%, y el 239Pu no existe en la naturaleza. Australia posee los mayores depósitos de uranio del mundo, con un 28% del total. Le siguen Kazajistán y Canadá. Estados Unidos sólo tiene el 3% de las reservas mundiales.

La mayoría de los reactores de fisión utilizan 235U , que se separa del 238U con cierto gasto. Esto se llama enriquecimiento. El método de separación más común es la difusión gaseosa de hexafluoruro de uranio (UF6) a través de membranas. Como el 235U tiene menos masa que el 238U, sus moléculas de UF6 tienen una mayor velocidad media a la misma temperatura y se difunden más rápidamente. Otra característica interesante del 235U es que absorbe preferentemente neutrones de movimiento muy lento (con energías de una fracción de eV), mientras que las reacciones de fisión producen neutrones rápidos con energías del orden de un MeV. Para fabricar un reactor de fisión autosostenible con 235U , es pues necesario ralentizar («termalizar») los neutrones. El agua es muy eficaz, ya que los neutrones chocan con los protones de las moléculas de agua y pierden energía. La figura 4 muestra un esquema de un diseño de reactor, llamado reactor de agua presurizada.

Figura 4. Un reactor de agua presurizada está ingeniosamente diseñado para controlar la fisión de grandes cantidades de 235U , al tiempo que utiliza el calor producido en la reacción de fisión para crear vapor para generar energía eléctrica. Las barras de control ajustan el flujo de neutrones de manera que se obtenga la criticidad, pero sin superarla. En caso de que el reactor se sobrecaliente y haga hervir el agua, la reacción en cadena termina, ya que el agua es necesaria para termalizar los neutrones. Esta característica de seguridad inherente puede verse superada en circunstancias extremas.

Las barras de control que contienen núclidos que absorben muy fuertemente los neutrones se utilizan para ajustar el flujo de neutrones. Para producir una gran potencia, los reactores contienen de cientos a miles de masas críticas, y la reacción en cadena se vuelve fácilmente autosostenible, una condición llamada criticidad. El flujo de neutrones debe regularse cuidadosamente para evitar un aumento exponencial de las fisiones, una condición llamada supercriticidad. Las barras de control ayudan a evitar el sobrecalentamiento, e incluso una fusión o un desmontaje explosivo. El agua que se utiliza para termalizar los neutrones, necesaria para que induzcan la fisión en el 235U, y lograr la criticidad, proporciona una retroalimentación negativa para los aumentos de temperatura. En caso de que el reactor se sobrecaliente y haga hervir el agua hasta convertirla en vapor o se produzca una ruptura, la ausencia de agua acaba con la reacción en cadena. Sin embargo, los productos de fisión radiactivos del reactor pueden seguir generando un calor considerable. Por lo tanto, es necesario incorporar otras características de seguridad en caso de un accidente con pérdida de refrigerante, incluyendo agua de refrigeración auxiliar y bombas.

Un nucleido ya mencionado es el 239Pu, que tiene una vida media de 24.120 años y no existe en la naturaleza. El plutonio-239 se fabrica a partir del 238U en los reactores, y ofrece la oportunidad de utilizar el otro 99% del uranio natural como fuente de energía. La siguiente secuencia de reacción, llamada reproducción, produce 239Pu. La reproducción comienza con la captura de neutrones por parte del 238U :

El uranio-239 se desintegra entonces β-:

239U → 239Np + β- + ve(t1/2 = 23 min).

El neptunio-239 también se desintegra por β-:

239Np → 239Pu + β- + ve(t1/2 = 2,4 d).

El plutonio-239 se acumula en el combustible del reactor a un ritmo que depende de la probabilidad de captura de neutrones por el 238U (todo el combustible del reactor contiene más 238U que 235U). Los reactores diseñados específicamente para producir plutonio se denominan reactores reproductores. Parecen ser intrínsecamente más peligrosos que los reactores convencionales, pero aún se desconoce si sus riesgos pueden hacerse económicamente aceptables. Los cuatro reactores de Chernóbil, incluido el que fue destruido, se construyeron para fabricar plutonio y producir electricidad. Estos reactores tenían un diseño significativamente diferente del reactor de agua presurizada ilustrado anteriormente. El plutonio-239 tiene ventajas sobre el 235U como combustible de reactor: produce más neutrones por fisión de media y es más fácil que un neutrón térmico provoque su fisión. También es químicamente diferente del uranio, por lo que es intrínsecamente más fácil de separar del mineral de uranio. Esto significa que el 239Pu tiene una masa crítica particularmente pequeña, una ventaja para las armas nucleares.

Exploraciones PhET: Fisión nuclear

Iniciar una reacción en cadena, o introducir isótopos no radiactivos para evitarla. Controla la producción de energía en un reactor nuclear

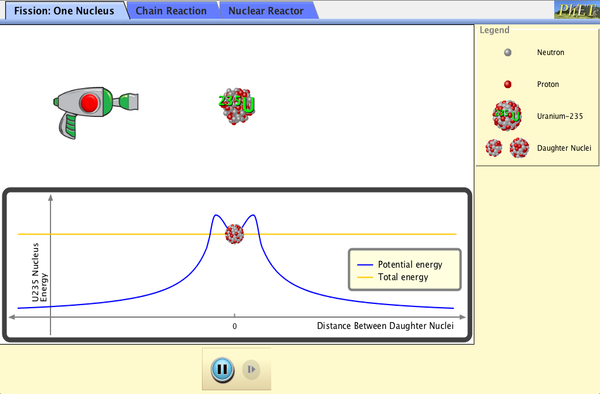
Haz clic para descargar la simulación. Ejecutar utilizando Java.

Resumen de la sección

• La fisión nuclear es una reacción en la que un núcleo se divide.
• La fisión libera energía cuando los núcleos pesados se dividen en núcleos de masa media.
• La fisión autosostenida es posible, porque la fisión inducida por neutrones también produce neutrones que pueden inducir otras fisiones, n + AX → FF1 + FF2 + xn, donde FF1 y FF2 son los dos núcleos hijos, o fragmentos de fisión, y x es el número de neutrones producidos.
• Una masa mínima, llamada masa crítica, debe estar presente para alcanzar la criticidad.
• Más de una masa crítica puede producir supercriticidad.
• La producción de isótopos nuevos o diferentes (especialmente el 239Pu) por transformación nuclear se llama reproducción, y los reactores diseñados para este fin se llaman reactores reproductores.