No es frecuente que una ecuación matemática llegue a la prensa nacional, ni mucho menos a la radio popular, ni que, lo más sorprendente de todo, sea objeto de debate en el parlamento británico. Sin embargo, en 2003 la vieja ecuación cuadrática, que todos aprendimos en la escuela, fue todo eso.
Por dónde empezamos

Todo empezó en una reunión del Sindicato Nacional de Profesores. La ecuación cuadrática se alzó ante la nación como ejemplo de la cruel tortura infligida por los matemáticos a los pobres escolares desprevenidos. Intrigada por esta acusación, la ecuación cuadrática aceptó un papel estelar en la radio en horario de máxima audiencia, donde fue cuestionada por un formidable entrevistador más acostumbrado a enfrentarse al Primer Ministro. El Times (de Londres) ocupó un espacio en su columna de líder, más reservada normalmente a los debates de peso sobre la salud moral (o no) del mundo moderno, para proclamar que la ecuación cuadrática era inútil, que las matemáticas eran inútiles y que, de todos modos, nadie quería estudiar matemáticas, así que para qué molestarse. Preocupados por que las peligrosas admisiones de la ecuación cuadrática quedaran sin respuesta, se debatió la importancia vital de la ecuación para la supervivencia del Reino Unido (se adoptó una opinión positiva, les alegrará saber) en la Cámara de los Comunes británica.
¿Dónde acabaría todo esto? ¿Estaba realmente muerta la ecuación cuadrática? ¿Le importaba a alguien? ¿Son los matemáticos realmente monstruos malvados que sólo quieren infligir ecuaciones cuadráticas a una generación más joven como medio de corromper sus almas inmortales?
Tal vez sea así, pero no es realmente culpa de la ecuación cuadrática. De hecho, la ecuación cuadrática ha desempeñado un papel fundamental no sólo en toda la civilización humana tal como la conocemos, sino en la posible detección de otras civilizaciones extraterrestres e incluso en actividades modernas tan vitales como ver la televisión por satélite. ¿Qué otra cosa, aparte de la naturaleza de la revelación divina, podría considerarse que ha tenido tal impacto en la vida tal como la conocemos? De hecho, en un sentido muy real, las ecuaciones cuadráticas pueden salvarte la vida.
Los babilonios
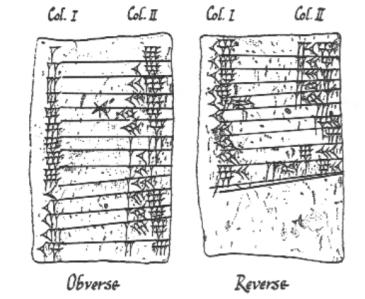
Las tablillas cuneiformes babilónicas que registran las 9 tablas de multiplicar
Todo comenzó alrededor del año 3000 a.C. con los babilonios. Fueron una de las primeras civilizaciones del mundo y aportaron grandes ideas como la agricultura, la irrigación y la escritura. Trazaron las trayectorias del Sol, la Luna y los planetas, y las registraron en tablillas de arcilla (que aún pueden verse en el Museo Británico). A los babilonios les debemos las ideas modernas sobre los ángulos, incluida la forma en que el círculo se divide en 360 grados (debido a un pequeño error de cálculo, uno por día). También debemos a los babilonios la invención menos agradable del (temido) recaudador de impuestos. Y ésta era una de las razones por las que los babilonios necesitaban resolver ecuaciones cuadráticas.
Supongamos que usted es un granjero babilónico. En algún lugar de tu granja tienes un campo cuadrado en el que cultivas algo. ¿Qué cantidad de tu cosecha puedes cultivar en el campo? Duplique la longitud de cada lado del campo y verá que puede cultivar cuatro veces más que antes. La razón es que la cantidad de cultivo que puedes cultivar es proporcional al área del campo, que a su vez es proporcional al cuadrado de la longitud del lado. En términos matemáticos, si  es la longitud del lado del campo,
es la longitud del lado del campo, 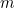 es la cantidad de cultivo que puedes cultivar en un campo cuadrado de longitud lateral 1, y
es la cantidad de cultivo que puedes cultivar en un campo cuadrado de longitud lateral 1, y  es la cantidad de cultivo que puedes cultivar, entonces
es la cantidad de cultivo que puedes cultivar, entonces
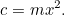 |
Esta es nuestra primera ecuación cuadrática, desnuda y parpadeante a la luz del sol. Las ecuaciones cuadráticas y las áreas están unidas como hermanos en la misma familia. Sin embargo, de momento no tenemos que resolver nada, ¡hasta que llegue el recaudador de impuestos! Alegremente le dice al agricultor «Quiero que me des cosechas para pagar los impuestos de tu finca». El agricultor tiene ahora un dilema: ¿qué tamaño de campo necesita para cultivar esa cantidad de cosecha? Nosotros podemos responder a esta pregunta fácilmente, de hecho
cosechas para pagar los impuestos de tu finca». El agricultor tiene ahora un dilema: ¿qué tamaño de campo necesita para cultivar esa cantidad de cosecha? Nosotros podemos responder a esta pregunta fácilmente, de hecho
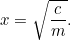 |
Hallar las raíces cuadradas utilizando una calculadora es fácil para nosotros, pero era más bien un problema para los babilonios. De hecho, desarrollaron un método de aproximación sucesiva a la respuesta que es idéntico al algoritmo (llamado método Newton-Raphson) que utilizan los ordenadores modernos para resolver problemas mucho más difíciles que las ecuaciones cuadráticas.
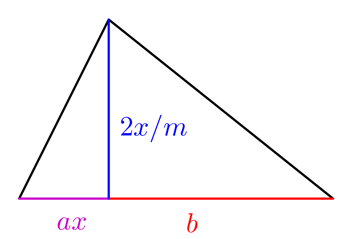
Ahora bien, no todos los campos son cuadrados. Supongamos ahora que el agricultor tiene un campo de forma más extraña con dos secciones triangulares como se muestra a la derecha.
Para valores adecuados de  y
y 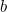 la cantidad de cosecha que el agricultor puede cultivar en este campo viene dada por
la cantidad de cosecha que el agricultor puede cultivar en este campo viene dada por
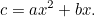 |
Esto se parece mucho más a la ecuación cuadrática a la que estamos acostumbrados, e incluso bajo la mirada maligna del hombre de los impuestos, es mucho más difícil de resolver. Sin embargo, los babilonios volvieron a dar con la respuesta. Primero dividimos por  para dar
para dar
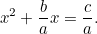 |
Ahora completamos el cuadrado utilizando el hecho de que
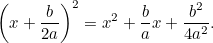 |
Combinando esto con la ecuación original tenemos
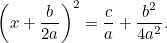 |
Esta es ahora una ecuación que podemos resolver sacando raíces cuadradas. El resultado es la famosa «fórmula 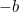 «:
«:
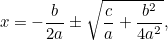 |
que se puede reescribir como
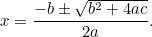 |
(La fórmula suele tener «-4ac» porque la ecuación cuadrática se escribe más habitualmente en la forma «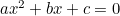 «.)
«.)
El hecho de que sacar una raíz cuadrada puede dar una respuesta positiva o negativa lleva al notable resultado de que una ecuación cuadrática tiene dos soluciones. Así que los rompecabezas matemáticos sólo tienen una solución.
Ahora bien, aquí es donde la enseñanza de las ecuaciones cuadráticas suele detenerse. Hemos llegado a ese objeto amado por todos los periodistas cuando entrevistan a los matemáticos: una fórmula. Se pueden inventar infinitas preguntas que impliquen poner valores de 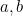 y
y  en la fórmula para dar (dos) respuestas. Pero esto no es en absoluto lo que son las matemáticas. Encontrar una fórmula es sólo el primer paso de un largo camino. Tenemos que preguntarnos qué significa la fórmula; qué nos dice sobre el universo; ¿importa realmente tener una fórmula? Veamos a dónde nos lleva esta fórmula.
en la fórmula para dar (dos) respuestas. Pero esto no es en absoluto lo que son las matemáticas. Encontrar una fórmula es sólo el primer paso de un largo camino. Tenemos que preguntarnos qué significa la fórmula; qué nos dice sobre el universo; ¿importa realmente tener una fórmula? Veamos a dónde nos lleva esta fórmula.
Una sorpresa para los griegos, un poco de papiroflexia matemática y sentido de la proporción
Avanzamos ahora 1000 años hasta los antiguos griegos y vemos qué hicieron con las ecuaciones cuadráticas. Los griegos eran magníficos matemáticos y descubrieron gran parte de las matemáticas que aún utilizamos hoy en día. Una de las ecuaciones que les interesaba resolver era la (simple) ecuación cuadrática
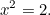 |

Sabían que esta ecuación tenía solución. En efecto, es la longitud de la hipotenusa de un triángulo rectángulo que tuviera lados de longitud uno.
Se deduce del teorema de Pitágoras que si un triángulo rectángulotriángulo acodado tiene los lados más cortos  y
y  y la hipotenusa
y la hipotenusa  entonces
entonces
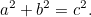 |
Poniendo 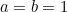 y
y  entonces
entonces 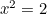 . Por lo tanto
. Por lo tanto 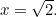
Entonces, ¿qué es  en este caso? O, para hacer la pregunta que hacían los griegos, ¿qué tipo de número es? La razón por la que esto importaba residía en el sentido de la proporción de los griegos. Creían que todos los números estaban en proporción entre sí. Para ser precisos, esto significaba que todos los números eran fracciones de la forma
en este caso? O, para hacer la pregunta que hacían los griegos, ¿qué tipo de número es? La razón por la que esto importaba residía en el sentido de la proporción de los griegos. Creían que todos los números estaban en proporción entre sí. Para ser precisos, esto significaba que todos los números eran fracciones de la forma 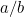 donde
donde  y
y  son números enteros. Números como 1/2, 3/4 y 355/113 son ejemplos de fracciones. Era natural esperar que
son números enteros. Números como 1/2, 3/4 y 355/113 son ejemplos de fracciones. Era natural esperar que  fuera también una fracción. La gran sorpresa fue que no lo es. De hecho
fuera también una fracción. La gran sorpresa fue que no lo es. De hecho
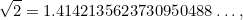 |
donde los puntos  significan que la expansión decimal de
significan que la expansión decimal de  continúa hasta el infinito sin ningún patrón discernible. (Volveremos a encontrarnos con esta situación más adelante cuando aprendamos sobre el caos.)
continúa hasta el infinito sin ningún patrón discernible. (Volveremos a encontrarnos con esta situación más adelante cuando aprendamos sobre el caos.)
 fue el primer número irracional (es decir, un número que no es una fracción, o racional), en ser reconocido como tal. Otros ejemplos son
fue el primer número irracional (es decir, un número que no es una fracción, o racional), en ser reconocido como tal. Otros ejemplos son 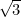 ,
,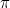 ,
,  y, de hecho, «la mayoría» de los números. Hubo que esperar hasta el siglo XIX para tener una buena forma de pensar en estos números. El descubrimiento de que
y, de hecho, «la mayoría» de los números. Hubo que esperar hasta el siglo XIX para tener una buena forma de pensar en estos números. El descubrimiento de que  no era un número racional provocó una gran emoción (se sacrificaron 100 bueyes por ello) y una gran conmoción, ya que el descubridor tuvo que suicidarse. (¡Que esto sea una terrible advertencia para los aficionados a las matemáticas!) En ese momento, los griegos abandonaron el álgebra y se dedicaron a la geometría.
no era un número racional provocó una gran emoción (se sacrificaron 100 bueyes por ello) y una gran conmoción, ya que el descubridor tuvo que suicidarse. (¡Que esto sea una terrible advertencia para los aficionados a las matemáticas!) En ese momento, los griegos abandonaron el álgebra y se dedicaron a la geometría.
Lejos de ser un número oscuro, nos encontramos con  regularmente: cada vez que utilizamos un trozo de papel A4. En Europa, los tamaños de papel se miden en tamaños A, siendo A0 el más grande con una superficie de
regularmente: cada vez que utilizamos un trozo de papel A4. En Europa, los tamaños de papel se miden en tamaños A, siendo A0 el más grande con una superficie de 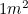 . Los tamaños A tienen una relación especial entre ellos. Si ahora hacemos un poco de origami, tomando una hoja de papel A1 y doblándola por la mitad (por su lado más largo), obtenemos el papel A2. Si se vuelve a doblar por la mitad, se obtiene el A3, y de nuevo el A4, etc. Sin embargo, el papel está diseñado para que las proporciones de cada uno de los tamaños A sean las mismas, es decir, cada trozo de papel tiene la misma forma.
. Los tamaños A tienen una relación especial entre ellos. Si ahora hacemos un poco de origami, tomando una hoja de papel A1 y doblándola por la mitad (por su lado más largo), obtenemos el papel A2. Si se vuelve a doblar por la mitad, se obtiene el A3, y de nuevo el A4, etc. Sin embargo, el papel está diseñado para que las proporciones de cada uno de los tamaños A sean las mismas, es decir, cada trozo de papel tiene la misma forma.
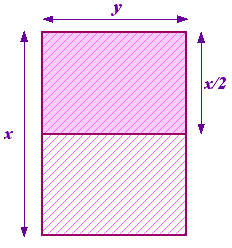
Podemos plantear la cuestión de qué proporción es ésta. Empieza con un trozo de papel con los lados x e y, siendo x el lado más largo. Ahora divídelo en dos para obtener otro trozo de papel con lados y y x/2, siendo ahora y el lado más largo. Esto se ilustra a la derecha.
Las proporciones del primer trozo de papel son 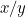 y las del segundo son
y las del segundo son 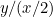 o
o 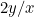 . Queremos que estas dos proporciones sean iguales. Esto significa que
. Queremos que estas dos proporciones sean iguales. Esto significa que
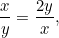 |
o
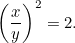 |
¡Otra ecuación cuadrática! Afortunadamente es una que ya hemos conocido. Al resolverla encontramos que
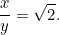 |
Este resultado es fácil de comprobar. Basta con tomar una hoja de papel A4 (o A3 o A5) y medir los lados. También podemos calcular el tamaño de cada hoja. El área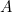 de un trozo de papel A0 viene dada por
de un trozo de papel A0 viene dada por
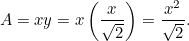 |
Pero sabemos que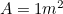 así que tenemos otra ecuación cuadrática para el lado más largo
así que tenemos otra ecuación cuadrática para el lado más largo de A0, dada por
de A0, dada por
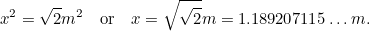 |
Esto significa que el lado más largo de A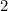 está dado por
está dado por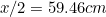 (¿por qué?) y el de A
(¿por qué?) y el de A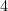 por
por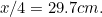 . Comprueba esto en tus propias hojas de papel.
. Comprueba esto en tus propias hojas de papel.
El papel utilizado en Estados Unidos, llamado foolscap, tiene una proporción diferente. Para ver por qué, volvemos a los griegos y a otra ecuación cuadrática. Después de haber causado tanto dolor, la ecuación cuadrática se redime en la búsqueda de las proporciones perfectas: una búsqueda que continúa hoy en día en el diseño de los decorados de las películas, y que se puede ver en muchos aspectos de la naturaleza.
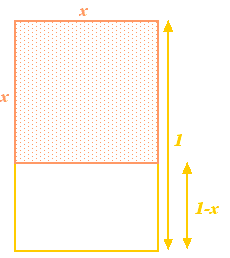
Empecemos con un rectángulo, y luego quitemos de él un cuadrado con la misma longitud de lado que el lado más corto del rectángulo. Si el lado más largo del rectángulo tiene longitud 1 y el lado más corto tiene longitud  , entonces el cuadrado tiene lados de longitud
, entonces el cuadrado tiene lados de longitud  . Al quitarlo del rectángulo se obtiene un rectángulo más pequeño con el lado más largo
. Al quitarlo del rectángulo se obtiene un rectángulo más pequeño con el lado más largo  y el más pequeño
y el más pequeño 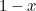 . Hasta aquí, todo muy abstracto. Sin embargo, los griegos creían que el rectángulo que tenía las proporciones más estéticas (el llamado Rectángulo de Oro) era aquel en el que los rectángulos grande y pequeño construidos anteriormente tenían las mismas proporciones. Para que esto sea posible debemos tener
. Hasta aquí, todo muy abstracto. Sin embargo, los griegos creían que el rectángulo que tenía las proporciones más estéticas (el llamado Rectángulo de Oro) era aquel en el que los rectángulos grande y pequeño construidos anteriormente tenían las mismas proporciones. Para que esto sea posible debemos tener
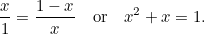 |
Esta es otra ecuación cuadrática: una muy importante que aparece en todo tipo de aplicaciones. Tiene la solución (positiva)
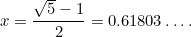 |
El número  se llama proporción áurea y se suele denotar con la letra griega
se llama proporción áurea y se suele denotar con la letra griega 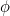 .
.

El rectángulo áureo puede verse en la forma de las ventanas, especialmente en las casas georgianas. Más recientemente, la proporción áurea también se puede encontrar como la «forma perfecta» de las fotografías e imágenes cinematográficas. La ecuación cuadrática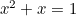 también aparece en los estudios de las poblaciones de conejos y en el patrón de disposición de las semillas de los girasoles y las hojas de los tallos de las plantas. Todo ello está relacionado con la proporción áurea a través de la secuencia de Fibonacci, que viene dada por
también aparece en los estudios de las poblaciones de conejos y en el patrón de disposición de las semillas de los girasoles y las hojas de los tallos de las plantas. Todo ello está relacionado con la proporción áurea a través de la secuencia de Fibonacci, que viene dada por
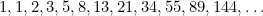 |

Semillas de girasol, dispuestas mediante los números de Fibonacci |
El Partenón, que encarna la proporción áurea |
En esta secuencia cada término es la suma de los dos anteriores. Fibonacci la descubrió en el siglo XV en un intento de predecir la futura población de conejos. Si se toma la relación de cada término con el que le sigue, se obtiene la secuencia de números
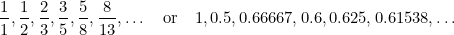 |
y estos números se acercan cada vez más a (lo has adivinado) la Razón Áurea 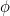 .
.
Encontrando las dos raíces de la ecuación cuadrática anterior podemos encontrar una fórmula para el enésimo término de la secuencia de Fibonacci. Si  es el
es el 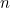 ésimo número con
ésimo número con 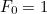 y
y 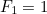 entonces
entonces  viene dado por la fórmula
viene dado por la fórmula
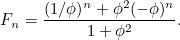 |
Los cónicos relacionan las ecuaciones cuadráticas con las estrellas

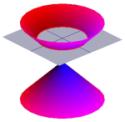
Los griegos también estaban muy interesados en la forma de los conos. la imagen de la izquierda muestra un cono típico.
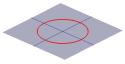
La mitad del cono se puede visualizar como la propagación de la luz procedente de una antorcha. Ahora bien, si se hace brillar una antorcha sobre una superficie plana, como una pared, se verán varias formas a medida que se mueve la antorcha. Estas formas se denominan secciones cónicas y son las curvas que se obtienen si se realiza un corte a través de un cono en varios ángulos diferentes. Precisamente estas curvas fueron estudiadas por los griegos, y reconocieron que había básicamente cuatro tipos de sección cónica. Si se toma una sección horizontal a través del cono, se obtiene un círculo. Una sección con un pequeño ángulo respecto a la horizontal da una elipse. Si se toma una sección vertical se obtiene una hipérbola y si se toma una sección paralela a un lado del cono se obtiene una parábola. Estas curvas se ilustran a continuación.
 |
 |
 |
 |
 |
 |
 |
 |

Una sección transversalsección de un cono puede ser un círculo … |

… una elipse … |
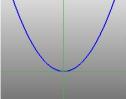
… una parábola … |
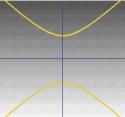
… o una hipérbola. |
Las secciones cónicas entran en nuestra historia porque cada una de ellas está descrita por una ecuación cuadrática. En particular, si 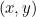 representa un punto de cada curva, entonces una ecuación cuadrática une
representa un punto de cada curva, entonces una ecuación cuadrática une  y
y 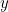 . Tenemos:
. Tenemos:
El círculo: 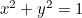 ;
;
La elipse: 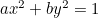 ;
;
La hipérbola: 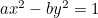 ;
;
La parábola: 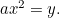
Estas curvas eran conocidas y estudiadas desde los griegos, pero aparte del círculo no parecían tener ninguna aplicación práctica. Sin embargo, como veremos en el próximo número de Plus, un vínculo entre las ecuaciones cuadráticas y las cónicas, unido a una poderosa casualidad, llevó a comprender el funcionamiento del universo, y en el siglo XVI llegó el momento en que las cónicas cambiaron el mundo.
Acerca de los autores
Chris Budd es catedrático de Matemáticas Aplicadas en el Departamento de Ciencias Matemáticas de la Universidad de Bath, y catedrático de Matemáticas en la Royal Institution de Londres.
Chris Sangwin es miembro del personal de la Escuela de Matemáticas y Estadística de la Universidad de Birmingham. Es becario de investigación en el centro de la Red de Apoyo al Aprendizaje y la Enseñanza de las Matemáticas, la Estadística y la Investigación Operativa.
Recientemente han escrito el libro de divulgación matemática Mathematics Galore!, publicado por Oxford University Press.
Este artículo se ha inspirado en parte en un notable debate en la Cámara de los Comunes británica sobre el tema de las ecuaciones cuadráticas. El registro de este debate puede encontrarse en Hansard, Cámara de los Comunes del Reino Unido, 26 de junio de 2003, Columnas 1259-1269, 2003, que está disponible en línea en el sitio web House of Commons Hansard Debate.