Lassen Sie uns zunächst die Division von Werten mit Exponenten untersuchen.
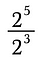
Erinnern Sie sich, dass Exponenten eine wiederholte Multiplikation darstellen. Wir können den obigen Ausdruck also umschreiben als:
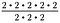
Da 2/2 = 1 ist, streichen wir drei Sätze von 2/2. Es bleibt 2 – 2 oder 2 zum Quadrat.
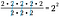
Natürlich können wir eine Abkürzung nehmen und die Anzahl der 2en unten von der Anzahl der 2en oben abziehen. Da diese Mengen durch ihre jeweiligen Exponenten dargestellt werden, müssen wir nur die gemeinsame Basis mit der Differenz der Exponentenwerte als Potenz schreiben.
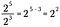
Wenn wir diese Regel verallgemeinern, haben wir folgendes, wobei n eine reelle Zahl ungleich Null darstellt und x und y ebenfalls reelle Zahlen sind.
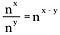
Erforschung der Nullpotenz
Von hier aus lässt sich leicht die Erklärung ableiten, warum jede von Null verschiedene Zahl, die mit der Nullpotenz erhöht wird, gleich 1 ist. Betrachten wir wieder ein konkretes Beispiel:
Wir wissen, dass jede Zahl ungleich Null, geteilt durch sich selbst, gleich 1 ist. Ich kann also folgendes schreiben:
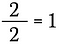
Das ist dasselbe wie zu schreiben:
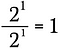
Nun verwende ich die Exponentenregel von oben, um die linke Seite dieser Gleichung umzuschreiben.
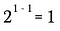
Natürlich ist dies äquivalent zu:
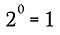
Wir können dasselbe Verfahren wie in diesem Beispiel zusammen mit der obigen verallgemeinerten Regel verwenden, um zu zeigen, dass jede reelle Zahl ungleich Null, die auf die Potenz Null erhöht wird, 1 ergeben muss.
Was ist mit Null hoch Null?
Hier wird es knifflig. Die obige Methode versagt, weil die Division durch Null natürlich ein No-No ist. Sehen wir uns an, warum das so ist.
Beginnen wir mit einem häufigen Fehler bei der Division durch Null.
Wie wäre es mit 2÷0? Schauen wir uns an, warum wir das nicht tun können.
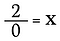
Die Division ist eigentlich nur eine Form der Multiplikation, was passiert also, wenn ich die obige Gleichung umschreibe als:
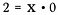
Welcher Wert könnte diese Gleichung für x erfüllen?
Es gibt keinen Wert! Jede Zahl mal Null ergibt Null, sie kann niemals gleich 2 sein. Deshalb sagen wir, dass die Division durch Null undefiniert ist. Es gibt keine mögliche Lösung.
Betrachten wir nun 0÷0.
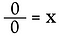
Schreiben wir es wieder als Multiplikationsproblem um.
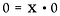
Hier haben wir eine ganz andere Situation. Die Lösung für x könnte eine beliebige reelle Zahl sein! Es gibt keine Möglichkeit zu bestimmen, was x ist. Daher gilt 0/0 als unbestimmt*, nicht als undefiniert.
Wenn wir versuchen, die obige Methode mit Null als Basis zu verwenden, um zu bestimmen, was Null hoch Null wäre, kommen wir sofort zum Stillstand und können nicht weitermachen, weil wir wissen, dass 0÷0 ≠ 1, aber unbestimmt ist.
Was bedeutet also Null hoch Null?
Dies ist sehr umstritten. Manche meinen, sie sollte als 1 definiert werden, andere meinen, sie sei 0, und wieder andere meinen, sie sei undefiniert. Für beide gibt es gute mathematische Argumente, und vielleicht ist es am besten, sie als unbestimmt zu betrachten.
Trotz dessen ist die mathematische Gemeinschaft dafür, Null hoch Null als 1 zu definieren, zumindest für die meisten Zwecke.
Vielleicht ist eine hilfreiche Definition von Exponenten für den Amateur-Mathematiker wie folgt: