Die Standardformel zur Bestimmung der Determinante einer 3×3-Matrix ist eine Zerlegung kleinerer 2×2-Determinantenprobleme, die sehr einfach zu handhaben sind. Wenn du eine Auffrischung brauchst, schau dir meine andere Lektion an, wie man die Determinante einer 2×2-Matrix findet. Nehmen wir an, wir haben eine quadratische Matrix A, bei der
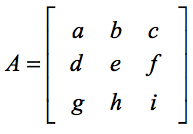
Die Determinante der Matrix A wird wie folgt berechnet:
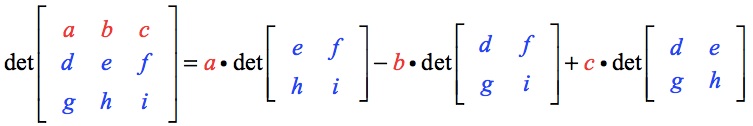
Hier sind die wichtigsten Punkte:
- Beachte, dass die Elemente der obersten Zeile, nämlich a, b und c, als skalare Multiplikatoren zu einer entsprechenden 2×2-Matrix dienen.
- Der Skalar a wird mit der 2×2-Matrix der übrig gebliebenen Elemente multipliziert, die entsteht, wenn vertikale und horizontale Liniensegmente durch a gezogen werden.
- Der gleiche Prozess wird angewandt, um die 2×2-Matrizen für die Skalarmultiplikatoren b und c zu konstruieren.
Determinante einer 3×3-Matrix (animiert)

Beispiele, wie man die Determinante einer 3×3-Matrix findet
Beispiel 1: Finde die Determinante der folgenden 3×3-Matrix.
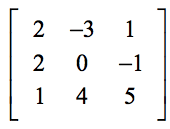
Der folgende Aufbau soll dir helfen, die Übereinstimmung zwischen den allgemeinen Elementen der Formel und den Elementen des eigentlichen Problems zu finden.
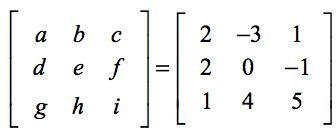
Wenden Sie die Formel an,


Beispiel 2: Berechnen Sie die Determinante der folgenden 3×3-Matrix.
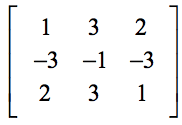
Sie müssen sehr vorsichtig sein, wenn Sie die Werte an den richtigen Stellen der Formel einsetzen. Häufige Fehler treten auf, wenn die Schüler beim Einsetzen der Werte unvorsichtig werden.
Nehmen Sie sich außerdem Zeit, um sicherzustellen, dass auch Ihre Berechnungen korrekt sind. Ein einziger Fehler irgendwo in der Rechnung führt sonst am Ende zu einer falschen Antwort.
Da,
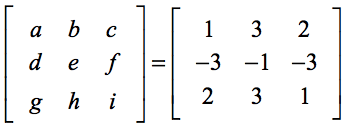
wird unsere Berechnung der Determinante…

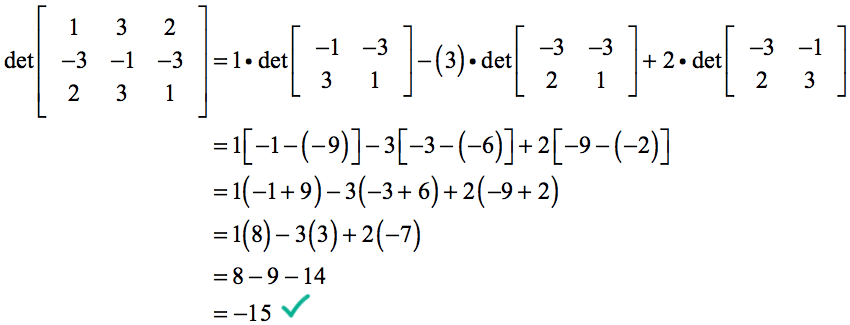
Beispiel 3: Löse die Determinante der folgenden 3×3 Matrix.
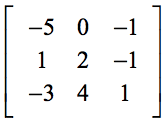
Das Vorhandensein von Null (0) in der ersten Zeile sollte unsere Berechnung viel einfacher machen. Denken Sie daran, dass die Elemente in der ersten Zeile als Skalarmultiplikatoren fungieren. Daher wird die Null multipliziert mit irgendetwas dazu führen, dass der gesamte Ausdruck verschwindet.