Začněme zkoumáním dělení hodnot pomocí exponentů.
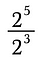
Připomeňme si, že exponenty představují opakované násobení. Výše uvedený výraz tedy můžeme přepsat jako:
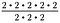
Protože 2/2 = 1, zrušíme tři sady 2/2. Tímto způsobem můžeme přepsat všechny tři sady. Zůstane 2 – 2, neboli 2 na druhou.
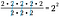
Můžeme to samozřejmě vzít zkratkou a odečíst počet 2 dole od počtu 2 nahoře. Protože tyto veličiny jsou reprezentovány příslušnými exponenty, stačí zapsat společný základ s rozdílem hodnot exponentu jako mocninu.
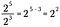
Pokud toto pravidlo zobecníme, máme následující, kde n představuje nenulové reálné číslo a x a y jsou také reálná čísla.
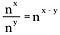
Vysvětlení nulové mocniny
Odtud lze snadno odvodit vysvětlení, proč se každé nenulové číslo zvýšené na nulovou mocninu rovná 1. Opět se podívejme na konkrétní příklad:
Víme, že každé nenulové číslo děleno sebou samým se rovná 1.
Podívejme se na konkrétní příklad. Mohu tedy napsat následující:
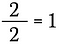
To je totéž, jako když napíšeme:
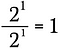
Nyní využiji pravidlo o exponentu z předchozího odstavce k přepsání levé strany této rovnice.
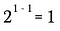
To je ovšem ekvivalentní:
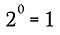
Můžeme použít stejný postup jako v tomto příkladu spolu s výše uvedeným zobecněným pravidlem, abychom ukázali, že každé nenulové reálné číslo zvýšené na mocninu nuly musí mít za výsledek 1.
A co nula na nultou mocninu?
Tady se věci stávají složitějšími. Výše uvedená metoda se rozbije, protože dělení nulou samozřejmě není možné. Prozkoumáme proč.
Začneme tím, že se podíváme na běžnou chybu dělení nulou.
Co třeba 2÷0? Podívejme se, proč to nemůžeme udělat.
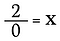
Dělení je vlastně jen forma násobení, takže co se stane, když výše uvedenou rovnici přepíšu jako:
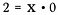
Jaká hodnota by mohla splňovat tuto rovnici pro x?
Neexistuje žádná hodnota! Jakékoli číslo vynásobené nulou vede k nule, nikdy se nemůže rovnat 2. Proto říkáme, že dělení nulou je neurčité. Neexistuje žádné možné řešení.
Nyní se podíváme na 0÷0.
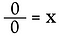
Znovu to přepíšeme jako úlohu na násobení.
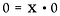
Tady se setkáváme se zcela jinou situací. Řešením pro x může být JAKÉKOLIV reálné číslo! Neexistuje žádný způsob, jak určit, co je x. Proto 0/0 považujeme za neurčité*, nikoliv neurčité.
Pokusíme-li se výše uvedenou metodou s nulou jako základem určit, co by byla nula na mocninu nuly, okamžitě se zastavíme a nemůžeme pokračovat, protože víme, že 0÷0 ≠ 1, ale je neurčité.
Takže čemu se rovná nula na mocninu nuly?
To je velmi diskutabilní. Někteří se domnívají, že by měla být definována jako 1, zatímco jiní si myslí, že je to 0, a někteří se domnívají, že je neurčitá. Pro každou z nich existují dobré matematické argumenty a možná je nejsprávnější považovat ji za neurčitou.
Přesto se matematická komunita přiklání k tomu, aby byla nula na mocnině nuly definována jako 1, alespoň pro většinu účelů.
Možná užitečná definice exponentů pro amatérského matematika je následující:
Podle mého názoru je nula na mocnině nuly rovno 1.