Úhel, který vznikne při obtočení poloměru
kolem kružnice:
 |
1 radián je přibližně 57,2958 stupně. |
Proč „57,2958…“ stupňů? To uvidíme za chvíli.
Radián je čistá míra vycházející z poloměru kružnice:
Radián: úhel, který vznikne, když vezmeme poloměr
a obtočíme jej kolem kružnice.
Radiány a stupně
Podívejme se, proč je 1 radián roven 57 stupňům.2958… stupňů:
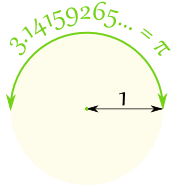
V půlkruhu jeπ radiánů, což je také 180°
Pro přechod z radiánů na stupně: vynásobte 180, vydělte π
Pro přechod ze stupňů na radiány: vynásobte π, vydělte 180
Tady je tabulka ekvivalentních hodnot:
| Stupně | Radiány (přesné) |
Radiány (přibližné) |
|---|---|---|
| 30° | π/6 | 0.524 |
| 45° | π/4 | 0,785 |
| 60° | π/3 | 1.047 |
| 90° | π/2 | 1,571 |
| 180° | π | 3.142 |
| 270° | 3π/2 | 4,712 |
| 360° | 2π | 6,283 |
Příklad: Kolik radiánů je v plném kruhu?
Představte si, že nastříháte kousky provázku přesně o délce od středu k obvodu kruhu …
… kolik kousků potřebujete, abyste jednou obešli kruh?
Odpověď: 2π (neboli asi 6,283 kousků provázku).
Matematiky preferované radiány
Protože radián vychází z čisté představy „poloměru položeného po obvodu“, dává při použití v matematice často jednoduché a přirozené výsledky.
Podívejte se například na funkci sinus pro velmi malé hodnoty:
Podívejte se například na funkci sinus pro velmi malé hodnoty

