Jednou z důležitých otázek je, jak jsou mezi celými čísly rozložena prvočísla? Odpověď je, velmi stručně řečeno, spíše náhodná, daná určitými základními statistickými údaji…
 Bill Casselman
Bill Casselman
Univerzita Britské Kolumbie ve Vancouveru, Kanada
Email Bill Casselman
| |
|
Úvod
Před mnoha lety se předpokládalo, že existuje nekonečný počet dvojic prvočísel $p$, $q$ s $q = p+2$. V poslední době došlo k určitému (a slavnému) pokroku v řešení tohoto problému. O nedávném pokroku se zmíním jen málo, ale místo toho se budu zabývat tím, co o takových dvojicích očekáváme – spíše než tím, co víme. Nic z toho, co řeknu, není nové a do jisté míry jsem pouze rozvinul to, co říká Andrew Granville ve své nedávné výkladové poznámce o nedávných pokrocích.
Kolik prvočísel očekáváme?
Prvočíslo je kladné celé číslo, které nemá žádné dělitele kromě sebe sama a $1$. Definice je jednoduchá, ale jakmile začneme zkoumat význam prvočísel, uvědomíme si, že vykazují mnohem subtilnější chování. Jednou z důležitých otázek je, jak jsou prvočísla rozložena mezi celými čísly? Odpověď je velmi stručná: spíše náhodně, vzhledem k určitým základním statistickým údajům. Co tím myslím?
No, zde je čtvercové pole zobrazující všechna prvočísla až do $400$:

V tomto poli jsou určité zákonitosti, z nichž některé okomentuji později. Většina z těch, které vnímáte, je způsobena nějakým artefaktem zobrazení. Například každý druhý sloupec je v podstatě prázdný, a to proto, že jediné sudé prvočíslo je $2$. Také každý pátý sloupec je v podstatě prázdný. Zajímavější jsou dvojice prvočísel (některé z nich nejsou tak viditelné, protože se rozdělují do dvou řádků, například $59$, $61$) a také některé vzory související s posledními zobrazenými číslicemi. Ty by se daly nazvat lokálními vzory. Žádné globální nejsou patrné.
Vynaložilo se mnoho úsilí na extrémně efektivní způsoby vytváření prvočísel, ale v dnešní době i velmi jednoduchý program potřebuje k vytvoření velkého seznamu prvočísel jen málo času. Jeden z nejplodnějších programů vytvoří velký seznam prvočísel a pak jej použije k výpočtu funkce $\pi(n)$, tedy počtu prvočísel $\le n$.
Jednou z věcí, ke které lze tento program použít, je získat přibližnou představu o četnosti prvočísel. V rozsahu $$ je $135$ prvočísel:
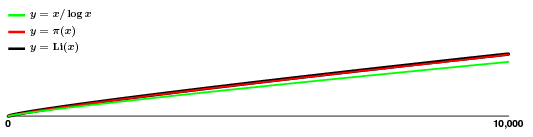
Aproximace vypadá skvěle! Takže i když $\pi(x)$ trochu poskakuje, zřejmě bez většího vzoru, máme pro něj docela dobrý odhad, což znamená, že máme dobrou představu o tom, jak prvočísla rostou, alespoň v průměru.
Je však třeba mít na paměti, že zdánlivá hladkost je ošidná. Zblízka vidíme, jak vypadají dvě horní křivky:

Komentář?
Heuristická úvaha o dvojčatech
Dvojčata jsou dvojice $p$, $p+2$, které jsou obě prvočísla. Například z jednoho z výše uvedených grafů vidíme dvojčata prvočísel $$ , , , , , , , , $$
a další. Byla vyslovena domněnka, že jich je nekonečně mnoho, ale přestože pro to existuje mnoho empirických důkazů, nebylo to dosud dokázáno.
Možná nejsilnějším důkazem je vzorec, který pozoruhodně dobře aproximuje počet $\pi_{2}(x)$ dvojčat prvočísel $\le x$. Nejsem si zcela jistý původem tohoto vzorce, ale poprvé se objevil v článku G. H. Hardyho a J. E. Littlewooda (sami dvojice dvojčat prvočísel) z roku 1923. Článek obsahuje několik podobných vzorců, všechny založené na stejné metodě, kterou použili k útoku na mnoho problémů již dříve. Jednalo se o jejich kruhovou metodu. Jejich odvození vzorce pro $\pi_{2}(x)$ není vůbec přísné, ale je velmi přesvědčivé. V dodatku k článku Andrewa Granvilla je o tom stručný popis.
Těsně po druhé světové válce však lord Cherwell (Frederick Lindemann) navrhl elementárnější pravděpodobnostní (a stále ne rigorózní) odvození. To vedlo ke spolupráci s E. M. Wrightem a nakonec ke společné posmrtné publikaci. To je vysvětleno v oddíle 22.20 známého Hardyho a Wrightova textu. Poněkud elementárnější verzi lze nalézt také v příloze Granvillova článku (oddíl 2.5). Navazuji na něj.
Východiskem pro věrohodnou úvahu je náš odhad pro $\pi(x)$, počet prvočísel menších nebo rovných $x$. Základní myšlenka odvození spočívá v tom, že prvočísla jsou do značné míry rozložena náhodně. Víme, že v okolí $x$ je hustota prvočísel přibližně $1/\log x$. Kdyby byla prvočísla rozložena náhodně, pak by pravděpodobnost, že dvě daná čísla v okolí $x$ jsou prvočísla, byla právě součinem lokálních pravděpodobností, což je $1/\log^{2} x$. To je jistě zvláštní úvaha, protože pokud $n > 2$, pravděpodobnost, že $n$ i $n+1$ jsou prvočísla, je $0$, zatímco skutečnost, že $p$ je prvočíslo, by zřejmě zvyšovala pravděpodobnost, že jím je $p+2$. Podobné úvahy je třeba brát v úvahu i kvůli možné dělitelnosti jinými malými prvočísly v okolí $x$.
V tomto příběhu je jeden jednoduchý fakt. Je-li $q$ libovolné prvočíslo, pak pravděpodobnost náhodného výběru celého čísla, které není dělitelné $q$, je $1-1/q$. Pravděpodobnost výběru dvou, která nejsou dělitelná $q$, je tedy součin $(1 – 1/q)^{2}$. Předpokládejme, že $p$ a $p+2$ jsou obě prvočísla, pak ani $p$, ani $p+2$ není dělitelné $q$. Pokud $q = 2$, stane se to v 1/2$ případů. Pokud $q \ne 2$, je pravděpodobnost, že $p \not\equiv 0$ a $p \not\equiv -2$ modulo $q$, $(1 – 2/q)$. Vzhledem k čínské zbytkové větě je dělitelnost dvěma prvočísly nezávislou událostí. Je-li tedy $x$ velké a $Q$ relativně malé, pravděpodobnost, že libovolná dvojice čísel $m$ a $n$ v blízkosti $x$ nebude násobkem žádného prvočísla až do $Q$, je $$ { 1\nad 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} } \, . $$
Nechť $\Gamma_{Q}$ je poměr této hodnoty k $\prod_{q \le Q}(1 – 2/q)$: $$ \Gamma_{Q} = { 1\nad 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \over (1 – 2/q) } $$ Máme $$ { 1 – 2/q \over (1-1/q)^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \over (1 – 1/q)^{2}. } = 1 – { 1 \over (q -1)^{2} } \, . $$ Standardní kritérium tvrdí, že tento součin konverguje, jestliže konverguje součet $\sum 1/(q-1)^{2}$. Ale konverguje, protože integrální test říká, že $\sum 1/n^{2}$ konverguje. Proto tento součin skutečně konverguje k číslu $\Pi_{\infty}$ jako $Q \rightarrow \infty$. Nechť $C_{2}$ je jeho inverzní hodnota. Oddíl 2.5 Granvillova článku říká, že v tomto bodě by mělo být intuitivně rozumné, že číslo $\pi_{2}(x)$ dvojčat prvočísel $\le x$ se aproximuje pomocí $$ \Pi_{2}(x) = C_{2}. \int_{2}^{\infty} { dx \over \log^{2} x } \, . $$
V textu Hardyho a Wrighta je uvedena pečlivější analýza, díky níž je intuitivní skok o něco jasnější.
Hodnotu konstanty zde před časem vypočítal J. W. Wrench na přibližně 1 $.32032363169373914785562422002911155686525 \ldots $. Zde je srovnání některých hodnot $\pi_{2}(x)$ a vzorce v rozsahu $$: $$ \matrix{ n & 10 000 & 20 000 & 30 000 & 40 000 & 50 000 \cr \pi_{2}(n) & 205\phantom{.0} & 342 \phantom{.0} & 467 \phantom{.0} & 591 \phantom{.0} & 705 \phantom{.0} & \cr \Pi_{2}(x) & 214,2 & 357,7 & 486,7 & 607,4 & 722,5 \cr } $$ $$ \matrix{ n & 60 000 & 70 000 & 80 000 & 90 000 & 100 000 \cr \pi_{2}(n) & 811 \phantom{.0} & 905 \phantom{.0} & 1007 \phantom{.0} & 1116 \phantom{.0} & 1224\phantom{.0} \cr \Pi_{2}(x) & 833,3 & 940,9 & 1045,7 & 1148,2 & 1248,7 \cr } $$
Komentář?
Dicksonova domněnka
Dvojčata jsou speciálním případem něčeho mnohem obecnějšího. Můžeme se ptát, zda existuje nekonečný počet dvojic $p$, $p+4$ nebo $p$, $p+6$, které jsou prvočísla? Nebo $p$, $p+10$? Případ $p$ a $p+10$ jistě naznačuje jeden z výše uvedených obrázků, na kterém jsou takové dvojice snadno viditelné. Co takhle nějaké trojice? Předpokládejme, že $a_{1}$, $a_{2}$, $\ldots$ , $a_{k}$ tvoří pole celých čísel. Můžeme očekávat, že existuje nekonečný počet množin $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$, z nichž všechny jsou prvočísla?“
Je třeba být trochu opatrný. Neexistují žádné prvočíselné dvojice tvaru $p$, $p+1$ (minulé $p = 2$), protože jedno z těchto dvou čísel musí být dělitelné $2$. Podobně za $p = 3$ neexistují žádné prvočíselné trojice $p$, $p+2$, $p+4$, protože jedno z nich musí být dělitelné $3$.
Tento poslední příklad by měl být poučný. Číslo $p+4$ je dělitelné $3$ tehdy a jen tehdy, když $p+1$ je dělitelné $3$. Tedy $3$ dělí jedno z čísel $p$, $p+2$, $p+4$ tehdy a jen tehdy, když dělí $p$, $p+1$, $p+2$. To se ale určitě stane, protože poslední trojice jasně pokrývá všechna čísla modulo $3$.
Obecně se říká, že $p$ je překážkou pro pole $(a_{i})$, jestliže $p$ vždy dělí alespoň jedno z každé posloupnosti $n+a_{i}$ ($i = 1$, $\ldots$, $k$). To nastane tehdy a jen tehdy, když čísla $a_{i} \; {\rm mod} \, p$ vyplňují celé $Z/p$.
To nemůže nikdy nastat, pokud $p > k$, takže k ověření, zda nějaké $p$ překáží $(a_{i})$, stačí ověřit, zda $a_{i}$ pokrývají $Z/p$ pro všechna $p \le k$. Pole $(a_{i})$ nazýváme přípustné, jestliže mu nepřekáží žádné prvočíslo.
Například $(1,3,7,9)$ je přípustné pole, protože, jak si můžete snadno ověřit, ani $2$, ani $3$ mu nepřekážejí. Několik prvočíselných posloupností zapadajících do tohoto vzoru je vidět na jednom z výše uvedených diagramů. Dalšími příklady jsou: (a) libovolné $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
Existují libovolně velké přípustné množiny. Ve skutečnosti:
Teorema. Jsou-li $a_{1}$ až $a_{k}$ libovolné množiny různých prvočísel $> k$, tvoří přípustnou množinu.
Proč tomu tak je? Je-li $p$ libovolné prvočíslo, kde $p> k$, pak jsme již viděli, že nemůže být překážkou. Jestliže však $p \le k$, pak nemůže dělit žádnou z množin $a_{i}$, z nichž žádná nemůže být kongruentní s $0$ modulo $p$. Takže $a_{i}$ nezaplňují $Z/p$.
Speciálním případem domněnky, kterou původně vyslovil L. E. Dickson, je, že pokud neexistují žádné prvočíselné obstrukce $(a_{i})$, pak existuje nekonečný počet prvočíselných posloupností tvaru $(n +a_{i})$.
Co se stalo v poslední době
Tady není místo na vyprávění celého příběhu, který byl důkladně popsán na jiných místech. Pro populární popis doporučuji zejména článek v časopise Quanta od Eriky Klarreichové a pro odbornější popis Granvillovu esej. Chtěl bych jen trochu přesněji než v popisu Klarreichové uvést, co je nejznámějším z nových výsledků.
Je to zásluha Yitanga Zhanga. Nejjednodušší vyjádření toho, co dokázal, je, že existuje nekonečný počet intervalů $[n, n+70 000 000)$ obsahujících alespoň dvě prvočísla. To je slabší než domněnka o dvojčatech prvočísel, ale koncepčně je jí velmi blízká. V pozdějších pracích (mnoha matematiků) byla velikost intervalu značně zmenšena, ale pravděpodobně neexistuje způsob, jak jej současnými metodami zmenšit na $2$.
Jak vysvětluje Granville, Zhangův první a pravděpodobně hlavní výsledek je, že existuje $k$ s vlastností, že pokud $a_{1}$, $\ldots$ , $a_{k}$ je přípustná množina $k$ prvků, pak existuje nekonečný počet $n$ takových, že $\{ n +a_{i}$ \}$ obsahuje alespoň dvě prvočísla. (V Klarreichově článku Quanta se tato množina nazývá „hřeben“. Nezapomeňte, že podle Dicksonovy domněnky bychom očekávali, že budeme moci říci, že všech $k$ jsou prvočísla.) Ve skutečnosti Zhang dokázal, že toto tvrzení je pravdivé pro konkrétní $k =3 500 000$ pokrývající interval 70 000 000$. Dnes již slavným důsledkem je pro nějaké $m \lt 70 000 000$, že existuje nekonečný počet dvojic prvočísel $p$, $p+m$.
Čteme dále
- Lord Cherwell a E. M. Wright, „The frequency of prime patterns“, The Quarterly Journal of Mathematics 11 (1960).
Ti, kdo vědí něco o životě lorda Cherwella, jinak známého jako Frederick Lindemann, budou velmi překvapeni, když se dozvědí o jeho přínosu k teorii čísel. Životopis na Wikipedii dostatečně nenaznačuje všechny důvody jeho špatné pověsti hlavního vědeckého poradce Churchilla za druhé světové války.
- L. E. Dickson, „A new extension of Dirichlet’s theorem on prime numbers“, Messenger of Mathematics 33.
Viz také heslo o Dicksonově domněnce na Wikipedii.
- Andrew Granville, „Primes in intervals of bounded length“ (Prvočísla v intervalech omezené délky). Dostupné z jeho domovské stránky.
- G. H. Hardy, Ramanujan, Cambridge University Press.
Odddíl 2.5 obsahuje ideální odvození možného vzorce pro $\pi(x)$.
- G. H. Hardy a J. E. Hardy. Littlewood, „Some problems of ‚Partitio numerorum‘ III: on the expression of a number as a sum of primes“, Acta Mathematica 44 (1923).
- G. H. Hardy a E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, „Together and alone, closing the prime gap“, Quanta 19. listopadu 2013.
- B. Hardy, „The theory of numbers“, Oxford Press.
- Erica Klarreich, „Together and alone, closing the prime gap“, Quanta 19. listopadu 2013. Riemann, „On the number of prime numbers less than a given quantity“ (O počtu prvočísel menších než daná veličina). Anglický překlad tohoto klasického díla od Davida Wilkinse je k dispozici na odkazu ve Wikipedii.
Mimo jiné je zde nastíněno odvození přibližného vzorce pro $\pi(x)$.
- J. W. Wrench, „Evaluation of Artin’s constant and the twin-prime constant“, Mathematics of Computation 76 (1961).
Raný výpočet $C_{2}$.
- Seznam prvočísel do 1 000 000 000 000$
- Seznam prvních 20 000 dvojčísel.
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Kanada
Email Bill Casselman
.